

Quadrate ungerader Zahlen
Vor kurzem entdeckte ich in einer Sammlung mathematischer Zitate folgenden Ausspruch:
Ich wenigstens kenne keine vollbefriedigende Erklärung dafür, warum jede ungerade Zahl (von 3 ab), mit sich selbst multipliziert, stets ein Vielfaches von 8 mit 1 als Rest ergibt.
Erich Bischoff, Mystik und Magie der Zahlen, 1920
Bevor ich einige Vorschläge zur "Erklärung" dieser Tatsache anbiete, verweise ich, was den Inhalt des Buches angeht, auf eine Rezension aus dem Medienportal roterdorn, mit der ich mindestens darin übereinstimme, dass der Author Erich Bischoff wohl der Mathematik nicht allzu nahe stand; und das kann ich sogar "beweisen".
Denn die obige Behauptung, die dort ab 3 aufgestellt wurde, gilt freilich auch für 1; schließlich ist auch die Null (12 : 8 = 0 Rest 1) ein Vielfaches von 8 (0 * 8 = 0).
Aber nun zu der Erklärung als solcher, aber was heißt eigentlich Erklärung? Der Mathematiker erwartet einen Beweis, dann ist er zufrieden. Was dagegen ist eine Erklärung, noch dazu eine vollbefriedigende?
Ich trau mich mal, indem ich etwas Geometrie bemühe.
Dazu schneide ich mir mal eine 1 aus dem Zahlenstrahl heraus, da ist sie: 0____1.
Und jetzt quadriere ich sie, was geometrisch ein Quadrat ergibt:
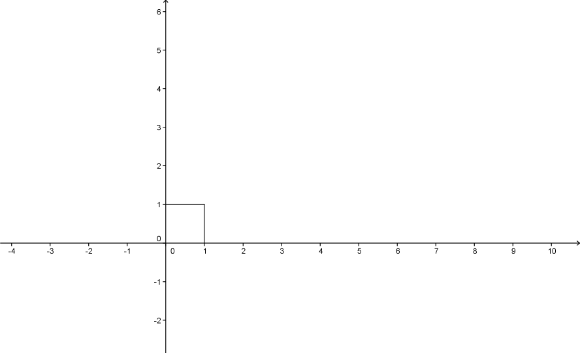
Dafür stimmt unsere Aussage ja schon, siehe oben. Die nächste ungerade Zahl ist die 3. Wir erweitern unser Bild auf ein Quadrat der Seitenlänge 3 und siehe da, es kommen 8 hier blau gezeichnete Quadrate hinzu:
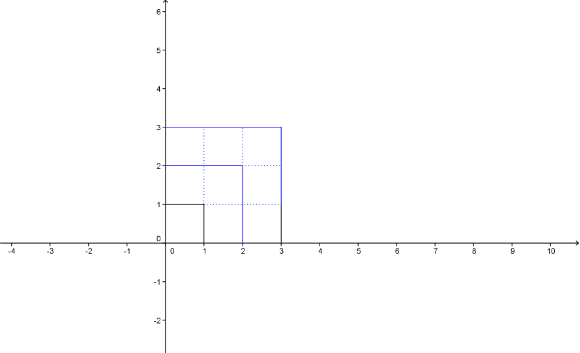
Im nächsten Schritt erweitern wir die Skizze auf das 5er-Quadrat:
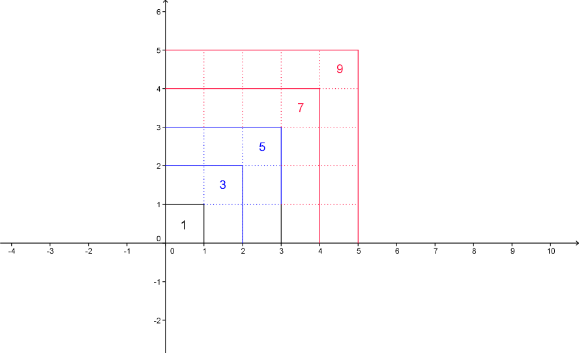
Und wenn man jetzt die in jedem Schritt hinzukommenden zwei Winkel betrachtet, dann wird schnell klar wie es weitergeht:
Wie unsere Tabelle zeigt, ergibt sich gerade die 8er - Reihe des Einmaleins als Zuwachs, oder anders ausgedrückt die Differenz zweier aufeinanderfolgender Zuwächse ist gerade 8. Dies ist aber nichts anderes, als die obige Behauptung, denn wenn man eine durch 8 teilbare Zahl um 8 erhöht, ist sie wieder durch 8 teilbar.
War das nun ein Beweis?
Nun das hängt vom Rigor (lat. Starrheit, Strenge) ab, den man bei der Beurteilung der Exaktheit eines Beweises anlegt.
Vergleichen wir mal, ist folgender Beweis besser?
Behauptung: Ergänzt man ein Quadrat mit ungerader Seitenlänge s zu einem Quadrat der Seitenlänge s + 2, so kommen 8 Quadrate der Seitenlänge 1 (Einheitsquadrate) mehr hinzu als der Zuwachs beim Schritt von s - 2 nach s beträgt.
Beweis:
(s + 2)2 - s2 =
s2 + 4s + 4 - s2 =
s2 - (s2 - 4s + 4) + 8 =
s2 - (s - 2)2 + 8
Das wollte ich beweisen; aber, Moment mal! Es ist immer verdächtig, wenn eine Voraussetzung nicht zum Beweis verwendet wurde und das ist hier der Fall. Die obige Berechnung klappt auch, wenn s gerade ist, die Voraussetzung s ungerade wurde nicht verwendet!
Tatsächlich stimmt die Behauptung auch für gerade s, aber, um zur Ausgangsaufgabe zurück zu kommen, der Start der Geschichte gelingt nur für ungerade s, z.B. für s = 1. Hier ergibt sich die in obiger Tabelle aufgeschriebene 8er Reihe für die Zuwächse. Bei jeder geraden Zahl als Startwert erhält man keine durch 8 teilbaren Zuwächse (z.B. 2*2=4, 12, 20, 28, ...).
Wäre Erich Bischoff jetzt befriedigter?
Schauen wir uns noch einen anderen Beweis an, der rein algebraischer Natur ist.
Eine ungerade Zahl u läßt sich allgemein immer in der Darstellung u = 2n + 1 schreiben mit einer natürlichen Zahl n, beispielsweise wäre 77 = 2*38 + 1.
Unsere Behauptung, dass das Quadrat einer ungeraden Zahl vermindert um 1 immer ein Vielfaches von 8 ist, kann also so geschrieben werden:
8 | (2n +1)2 - 1, wobei der senkrechte Strich | als "teilt" gelesen werde.
Um dies zu beweisen, formen wir um:
(2n + 1)2 - 1 = 4n2 + 4n = 4n(n + 1)
4 ist also immer ein Faktor unserer rechten Seite obiger Formel; aber man sieht noch mehr, denn zusätzlich ist eine von den beiden Zahlen n oder n+1 jedenfalls eine gerade Zahl und damit steckt auch noch eine weitere 2 als Faktor in dem umgeformten Ausdruck, was insgesamt einen Faktor 8 ergibt. Das ist aber gerade die Behauptung.
Vollbefriedigende Erklärung?
Die Grafiken dieser Seite wurden mit GeoGebra erstellt.
Ich wenigstens kenne keine vollbefriedigende Erklärung dafür, warum jede ungerade Zahl (von 3 ab), mit sich selbst multipliziert, stets ein Vielfaches von 8 mit 1 als Rest ergibt.
Erich Bischoff, Mystik und Magie der Zahlen, 1920
Bevor ich einige Vorschläge zur "Erklärung" dieser Tatsache anbiete, verweise ich, was den Inhalt des Buches angeht, auf eine Rezension aus dem Medienportal roterdorn, mit der ich mindestens darin übereinstimme, dass der Author Erich Bischoff wohl der Mathematik nicht allzu nahe stand; und das kann ich sogar "beweisen".
Denn die obige Behauptung, die dort ab 3 aufgestellt wurde, gilt freilich auch für 1; schließlich ist auch die Null (12 : 8 = 0 Rest 1) ein Vielfaches von 8 (0 * 8 = 0).
Aber nun zu der Erklärung als solcher, aber was heißt eigentlich Erklärung? Der Mathematiker erwartet einen Beweis, dann ist er zufrieden. Was dagegen ist eine Erklärung, noch dazu eine vollbefriedigende?
Ich trau mich mal, indem ich etwas Geometrie bemühe.
Dazu schneide ich mir mal eine 1 aus dem Zahlenstrahl heraus, da ist sie: 0____1.
Und jetzt quadriere ich sie, was geometrisch ein Quadrat ergibt:

Dafür stimmt unsere Aussage ja schon, siehe oben. Die nächste ungerade Zahl ist die 3. Wir erweitern unser Bild auf ein Quadrat der Seitenlänge 3 und siehe da, es kommen 8 hier blau gezeichnete Quadrate hinzu:

Im nächsten Schritt erweitern wir die Skizze auf das 5er-Quadrat:

Und wenn man jetzt die in jedem Schritt hinzukommenden zwei Winkel betrachtet, dann wird schnell klar wie es weitergeht:
| Seitenlänge | Zuwachs | = | Differenz |
| 1 |
3 + 5 |
8 |
|
| 3 |
7 + 9 |
16 |
8 |
| 5 | 11 + 13 | 24 | 8 |
| 7 | 15 + 17 | 32 | 8 |
| 9 | 19 + 21 | 40 | 8 |
| 11 | 23 + 25 | 48 | 8 |
| 13 | 27 + 29 | 56 | 8 |
Wie unsere Tabelle zeigt, ergibt sich gerade die 8er - Reihe des Einmaleins als Zuwachs, oder anders ausgedrückt die Differenz zweier aufeinanderfolgender Zuwächse ist gerade 8. Dies ist aber nichts anderes, als die obige Behauptung, denn wenn man eine durch 8 teilbare Zahl um 8 erhöht, ist sie wieder durch 8 teilbar.
War das nun ein Beweis?
Nun das hängt vom Rigor (lat. Starrheit, Strenge) ab, den man bei der Beurteilung der Exaktheit eines Beweises anlegt.
Vergleichen wir mal, ist folgender Beweis besser?
Behauptung: Ergänzt man ein Quadrat mit ungerader Seitenlänge s zu einem Quadrat der Seitenlänge s + 2, so kommen 8 Quadrate der Seitenlänge 1 (Einheitsquadrate) mehr hinzu als der Zuwachs beim Schritt von s - 2 nach s beträgt.
Beweis:
(s + 2)2 - s2 =
s2 + 4s + 4 - s2 =
s2 - (s2 - 4s + 4) + 8 =
s2 - (s - 2)2 + 8
Das wollte ich beweisen; aber, Moment mal! Es ist immer verdächtig, wenn eine Voraussetzung nicht zum Beweis verwendet wurde und das ist hier der Fall. Die obige Berechnung klappt auch, wenn s gerade ist, die Voraussetzung s ungerade wurde nicht verwendet!
Tatsächlich stimmt die Behauptung auch für gerade s, aber, um zur Ausgangsaufgabe zurück zu kommen, der Start der Geschichte gelingt nur für ungerade s, z.B. für s = 1. Hier ergibt sich die in obiger Tabelle aufgeschriebene 8er Reihe für die Zuwächse. Bei jeder geraden Zahl als Startwert erhält man keine durch 8 teilbaren Zuwächse (z.B. 2*2=4, 12, 20, 28, ...).
Wäre Erich Bischoff jetzt befriedigter?
Schauen wir uns noch einen anderen Beweis an, der rein algebraischer Natur ist.
Eine ungerade Zahl u läßt sich allgemein immer in der Darstellung u = 2n + 1 schreiben mit einer natürlichen Zahl n, beispielsweise wäre 77 = 2*38 + 1.
Unsere Behauptung, dass das Quadrat einer ungeraden Zahl vermindert um 1 immer ein Vielfaches von 8 ist, kann also so geschrieben werden:
8 | (2n +1)2 - 1, wobei der senkrechte Strich | als "teilt" gelesen werde.
Um dies zu beweisen, formen wir um:
(2n + 1)2 - 1 = 4n2 + 4n = 4n(n + 1)
4 ist also immer ein Faktor unserer rechten Seite obiger Formel; aber man sieht noch mehr, denn zusätzlich ist eine von den beiden Zahlen n oder n+1 jedenfalls eine gerade Zahl und damit steckt auch noch eine weitere 2 als Faktor in dem umgeformten Ausdruck, was insgesamt einen Faktor 8 ergibt. Das ist aber gerade die Behauptung.
Vollbefriedigende Erklärung?
Die Grafiken dieser Seite wurden mit GeoGebra erstellt.