

Der Satz des Pythagoras
Ein ehemaliger Arbeitskollege, ebenfalls Mathematiker, machte mich vor einigen Jahren auf einen Beweis des Satzes von Pythagoras aufmerksam, den ich in dieser Form noch nicht kannte und aus dem man ein paar schöne Lehren für das Lehren von Mathematik ziehen kann.
Der Lehrer, der diesen Beweis in seiner Vorlesung brachte, war der zu unserer Studienzeit an der Universität Köln sehr bekannte Professor Dr. Peter Dombrowski, der als der reinste aller reinen Mathematiker in Köln und darüber hinaus galt und bei dem mein Arbeitskollege studiert hatte.
"Dem Reinen ist alles rein" heißt es in der Feuerzangenbowle von Heinrich Spoerl.
In Köln gab es eine regelrechte Rivalität zwischen Dombrowski und seinem angewandten Widerpart Prof. Dr. Johann Schröder, bei dem ich mein Diplom gemacht habe.
Was ist rein, was ist angewandt? Die Vorlesungen der beiden Dozenten zeigten deutlich, welch unterschiedlichen Rigor (s.o.) sie ansetzten. Nicht, dass Schröder weniger Exaktheit walten lies, an den entscheidenden Stellen war immer klar, worauf es ankam und wie die Quantoren gesetzt worden wären, wenn er sie hingeschrieben hätte.
Da Schröder keine Anfängervorlesungen las (außer gewöhnlichen Differentialgleichungen und Numerik, und die hörte man erst ab dem 3. Semester), war er auch nicht verpflichtet, mathematischen Anfängern formale Schreibweisen, aussagenlogische Grundlagen, Quantorenkalkül oder Epsilontik beizubringen; dass man das konnte setzte er voraus. Aber es geschah nie, dass man den Wald vor Bäumen nicht mehr erkennen konnte, man wusste, worauf es mathematisch ankam.
Genug nun der Vorrede. Wenden wir uns einem der bekanntesten Sätze der Mathematik zu.
Was und wie hat Dombo (wir hatten diesen Spitznamen für ihn) denn nun bewiesen:
Behauptung: sin² (x) + cos² (x) = 1 (*)
Pythagoras? Wieso Pythagoras, kannte der alte Grieche denn schon Sinus und Cosinus? Wohl kaum. Genauer nennt man diesen Satz auch oft den "trigonometrischen Satz des Pythagoras". Aber wenn man sich ins Gedächtnis ruft, wie der Sinus und der Cosinus im rechtwinkeligen Dreieck definiert sind, dann kommt man dem Pythagoras schon näher:
sin (x) = Gegenkathete / Hypotenuse, cos (x) = Ankathete / Hypotenuse
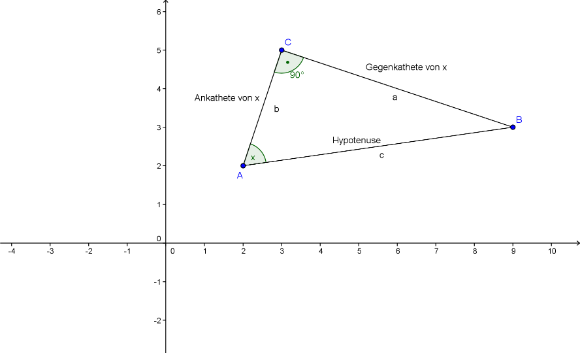
Übernimmt man aus der Zeichnung die Namen der Dreiecksseiten (Gegenkathete = a, Ankathete = b, Hypotenuse = c), so ergibt sich:
und mit c² auf beiden Seiten der Gleichung multipliziert gerade die bekannte Form a² + b² = c² des Satzes von Pythagoras.
Nun aber zum Beweis:
Bekanntlich sind Sinus und Cosinus Funktionen (auch) der reellen Analysis und zwar sehr schöne, sie sind auf ganz IR definiert und dort überall differenzierbar. Somit kann man die linke Seite obiger Gleichung (*) als Funktion f(x) auf IR auffassen (also f(x) = sin² (x) + cos² (x)) und einmal ableiten und erhält unter Anwendung der Kettenregel:
f’(x) = 2*sin(x)*cos(x) – 2*cos(x)*sin(x) = 0 für alle reellen x.
Das bedeutet, dass die erste Ableitung dieser Funktion f überall gleich 0 ist, was wiederum folgern lässt, dass f selber eine Konstante Funktion ist. Welche Konstante? Ganz einfach, wir berechnen:
f(0) = sin² (0) + cos² (0) = 0 + 1 = 1 und erhalten das gewünschte Ergebnis.
Genial einfach! Einfach genial!
Und nun?
Dies ist natürlich ernsthaft keine Methode den Satz des Pythagoras zu beweisen, wenn man nur dieses Ziel hat.
Die Menge an Mathematik, die man benötigt, um diesen Beweis so zu führen, ist mindestens so mächtig wie die Anzahl der Sandkörner, die Pythagoras benötigte um den geometrischen Beweis seines Satzes in den Sand zu malen. Denn der Weg von der euklidischen Geometrie zur Analysis ist weiter als man denkt.
Die Definition des Sinus (und anderer Funktionen) erfolgt in der Analysis häufig über die entsprechende Potenzreihe, was die gesamte Grenzwerttheorie der Analysis I bemüht. Daraus folgt zwar über den entsprechenden Satz sehr leicht, wie die 1. Ableitung (man braucht die Differentialrechnung), nämlich der Cosinus, aussieht, aber bis man daraus die Formel Gegenkathete / Hypotenuse hat, muss man eine Menge investieren.
Was meine ich damit?
Mathematik zu betreiben ist (auch) eine Sache der Werkzeuge, die man zum Zeitpunkt einer Beweisführung zur Hand hat. Mit Kanonen läßt sich leicht erfolgreich auf Spatzen schießen, mit einer Handschleuder muß man schon genau zielen und viel geübt haben, um zu treffen.
Und das Schießen mit Kanonen hat auch noch einen zweiten Nachteil: man muss aufpassen, dass man sich nicht selber trifft, will heißen, die Gefahr von Kreisschlüssen ist größer, also beim Beweis Aussagen zu verwenden, die die zu beweisende Aussage letzendlich irgendwo enthalten.
Die Grafiken dieser Seite wurden mit GeoGebra erstellt.
Der Lehrer, der diesen Beweis in seiner Vorlesung brachte, war der zu unserer Studienzeit an der Universität Köln sehr bekannte Professor Dr. Peter Dombrowski, der als der reinste aller reinen Mathematiker in Köln und darüber hinaus galt und bei dem mein Arbeitskollege studiert hatte.
"Dem Reinen ist alles rein" heißt es in der Feuerzangenbowle von Heinrich Spoerl.
In Köln gab es eine regelrechte Rivalität zwischen Dombrowski und seinem angewandten Widerpart Prof. Dr. Johann Schröder, bei dem ich mein Diplom gemacht habe.
Was ist rein, was ist angewandt? Die Vorlesungen der beiden Dozenten zeigten deutlich, welch unterschiedlichen Rigor (s.o.) sie ansetzten. Nicht, dass Schröder weniger Exaktheit walten lies, an den entscheidenden Stellen war immer klar, worauf es ankam und wie die Quantoren gesetzt worden wären, wenn er sie hingeschrieben hätte.
Da Schröder keine Anfängervorlesungen las (außer gewöhnlichen Differentialgleichungen und Numerik, und die hörte man erst ab dem 3. Semester), war er auch nicht verpflichtet, mathematischen Anfängern formale Schreibweisen, aussagenlogische Grundlagen, Quantorenkalkül oder Epsilontik beizubringen; dass man das konnte setzte er voraus. Aber es geschah nie, dass man den Wald vor Bäumen nicht mehr erkennen konnte, man wusste, worauf es mathematisch ankam.
Genug nun der Vorrede. Wenden wir uns einem der bekanntesten Sätze der Mathematik zu.
Was und wie hat Dombo (wir hatten diesen Spitznamen für ihn) denn nun bewiesen:
Behauptung: sin² (x) + cos² (x) = 1 (*)
Pythagoras? Wieso Pythagoras, kannte der alte Grieche denn schon Sinus und Cosinus? Wohl kaum. Genauer nennt man diesen Satz auch oft den "trigonometrischen Satz des Pythagoras". Aber wenn man sich ins Gedächtnis ruft, wie der Sinus und der Cosinus im rechtwinkeligen Dreieck definiert sind, dann kommt man dem Pythagoras schon näher:
sin (x) = Gegenkathete / Hypotenuse, cos (x) = Ankathete / Hypotenuse

Übernimmt man aus der Zeichnung die Namen der Dreiecksseiten (Gegenkathete = a, Ankathete = b, Hypotenuse = c), so ergibt sich:
$\mathtt{(\frac{a}{c})^2 + (\frac{b}{c})^2 = 1}$
Nun aber zum Beweis:
Bekanntlich sind Sinus und Cosinus Funktionen (auch) der reellen Analysis und zwar sehr schöne, sie sind auf ganz IR definiert und dort überall differenzierbar. Somit kann man die linke Seite obiger Gleichung (*) als Funktion f(x) auf IR auffassen (also f(x) = sin² (x) + cos² (x)) und einmal ableiten und erhält unter Anwendung der Kettenregel:
f’(x) = 2*sin(x)*cos(x) – 2*cos(x)*sin(x) = 0 für alle reellen x.
Das bedeutet, dass die erste Ableitung dieser Funktion f überall gleich 0 ist, was wiederum folgern lässt, dass f selber eine Konstante Funktion ist. Welche Konstante? Ganz einfach, wir berechnen:
f(0) = sin² (0) + cos² (0) = 0 + 1 = 1 und erhalten das gewünschte Ergebnis.
Genial einfach! Einfach genial!
Und nun?
Dies ist natürlich ernsthaft keine Methode den Satz des Pythagoras zu beweisen, wenn man nur dieses Ziel hat.
Die Menge an Mathematik, die man benötigt, um diesen Beweis so zu führen, ist mindestens so mächtig wie die Anzahl der Sandkörner, die Pythagoras benötigte um den geometrischen Beweis seines Satzes in den Sand zu malen. Denn der Weg von der euklidischen Geometrie zur Analysis ist weiter als man denkt.
Die Definition des Sinus (und anderer Funktionen) erfolgt in der Analysis häufig über die entsprechende Potenzreihe, was die gesamte Grenzwerttheorie der Analysis I bemüht. Daraus folgt zwar über den entsprechenden Satz sehr leicht, wie die 1. Ableitung (man braucht die Differentialrechnung), nämlich der Cosinus, aussieht, aber bis man daraus die Formel Gegenkathete / Hypotenuse hat, muss man eine Menge investieren.
Was meine ich damit?
Mathematik zu betreiben ist (auch) eine Sache der Werkzeuge, die man zum Zeitpunkt einer Beweisführung zur Hand hat. Mit Kanonen läßt sich leicht erfolgreich auf Spatzen schießen, mit einer Handschleuder muß man schon genau zielen und viel geübt haben, um zu treffen.
Und das Schießen mit Kanonen hat auch noch einen zweiten Nachteil: man muss aufpassen, dass man sich nicht selber trifft, will heißen, die Gefahr von Kreisschlüssen ist größer, also beim Beweis Aussagen zu verwenden, die die zu beweisende Aussage letzendlich irgendwo enthalten.
Die Grafiken dieser Seite wurden mit GeoGebra erstellt.