Der Turmbau zu Babylon
Dies ist ein Ausflug in die Architektur - für Mathematiker.
Dies ist ein Ausflug in die Mathematik - für Architekten.
Dies ist ein Ausflug in die Unendlichkeit - für alle.
Die Anregung zu der folgenden Darstellung erhielt ich durch eine Übungsaufgabe einer mathematischen Vorlesung an der BTU in Cottbus. Ich halte das Ergebnis für einigermaßen erstaunlich und außerhalb eines mathematischen Standpunktes für nur schwer akzeptabel und deshalb fasziniert mich diese Problemstellung.
Ich müsste in der Darstellung eine Menge mathematischer Grundlagen und Ergebnisse verwenden - unter anderem zum Begriff der Unendlichkeit - vielmehr werde ich versuchen, die notwendigen Schlüsse intuitiv und allgemein verständlich zu begründen, ohne dass ich allerdings der Versuchung widerstehen kann, hier und da ... meine Unendlichkeit besteht aus den berühmten drei Punkten ...
Worum geht es?
Wir bauen einen Turm, der aus einzelnen aufeinander gesetzten Würfeln bestehen soll. Die Würfel haben eine Kantenlänge von 1/n, wobei n bei 1 beginnend alle natürlichen Zahlen durchläuft: 1, 2, 3, ..., n, ...
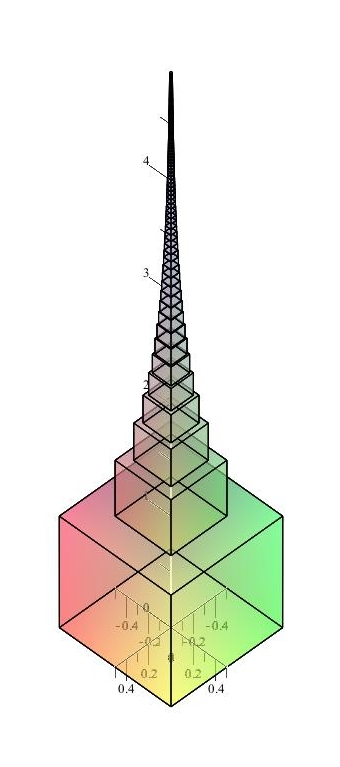
Das heißt, der unterste Würfel hat eine Kantenlänge von 1, der darauf 1/2, der darauf 1/3 und so weiter, höher und höher. Die Würfel sitzen mittig aufeinander, z. B. so wie in folgendem Bild gezeigt.
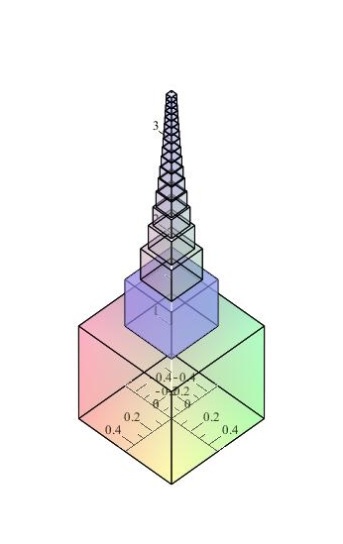
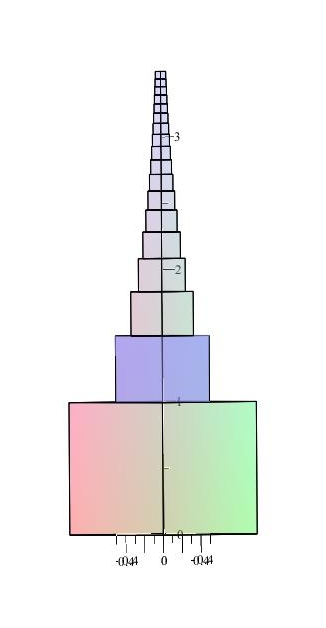
Die Zeichnungen enden mit dem 18ten Würfel, aber wir denken uns die weitere Fortsetzung nach oben.
Wie hoch würde der Turm, wenn man tatsächlich immer weiter (bis ins Unendliche, wo immer das ist) Würfel um Würfel aufeinander setzte? Jeder Würfel ist ja ein Stückchen kleiner als sein Vorgänger. Wird er immer höher, oder wird der immer kleiner werdende Zuwachs letztlich so gering, dass die Höhe des Turmes einem endlichen Wert entgegen strebt.
Mathematisch ausgedrückt ist unsere Fragestellung die nach dem Wert der unendlichen Summe
1 + 1/2 + 1/3 + 1/4 + 1/5 + ... + 1/n ... (*)
Ohne mathematische Einsichten mag man zunächst der Meinung sein, dass bei einer unendlichen Summation ja nur ein unendliches Ergebnis herauskommen kann.
Diese irrige Auffassung vertrat vor über 2000 Jahren bereits der griechische Philosoph Xenon, nach dem das Xenonsche Paradoxon benannt wurde.
Einschub für alle, die nicht glauben, dass eine Summe mit unendlich vielen Summanden einen endlichen Wert haben kann.
Er (Xenon) begründete, warum der zehnmal schnellere Achilles nicht in der Lage sei, eine Schildkröte einzuholen und zu überholen, die zunächst 1 Stadie Vorsprung vor ihm hat. Denn, so Xenon, wenn Achilles 1 Stadie zurückgelegt hat, dann legt in dieser Zeit, die Achilles braucht um 1 Stadie zu laufen, die Kröte selber 1/10 Stadie zurück. Während Achilles nun die 1/10 Stadie läuft, kommt die Kröte 1/100 Stadien weit und so weiter. Also hat die Schildkröte immer einen, wenn auch immer kleiner werdenden Vorsprung vor Achilles. ???????
Mathematisch ausgedrückt, die Summe
1 + 1/10 + 1/100 + 1/1000 + ... = 1 + 1/10 + 1/10² + 1/10³ + ... +1/10**n + ... (**)
hat einen unendlichen Wert, zumindest nach Xenon.
Nun ja, die Lebenserfahrung widerspricht dieser Überlegung, Achilles wird die Schildkröte ein- und überholen; also liegt die Vermutung nahe, dass die Summe (**) womöglich einen endlichen Zahlenwert hat, nämlich genau den, der der von Achilles zurückgelegten Strecke entspricht, bis er die Schildkröte eingeholt hat.
(Wie) kann man das berechnen?
Um zu einem Ergebnis zu kommen, überlegen wir uns, wie die Summanden obiger Addition als Dezimalzahlen aussehen.
1 + 1/10 + 1/100 + 1/1000 + ... = 1 + 0,1 + 0,01 + 0,001 + ... = 1,111...
mit anderen Worten die "Xenonsche" Summe ist eine unendliche periodische Dezimalzahl, nennen wir sie X := 1,111....
Hoppla, woher wissen wir denn, dass eine unendliche periodische Dezimalzahl einen endlichen Wert hat?
Auch das kann man durch Anwenden eines rechnerischen Kunstgriffs einsehen:
Wir multiplizieren unser Ergebnis X mit 10 und ziehen X davon ab, also:
10 * X 11,111... (Man multipliziert eine Dezimalzahl mit 10 indem man das Komma um eine Stelle nach rechts rückt.
= Die "Anzahl" der Einsen hinter dem Komma hat sich nicht geändert, es sind immer noch unendlich viele.)
- X - 1,111...
____________________
9 * X = 10 (Das Unverschämte ist, dass durch die Subtraktion der unendliche, periodische Anteil weg fällt, Stelle für Stelle; aber fangt ja nicht hinten an mit der schriftlichen Subtraktion. ;-)
Damit ist X = 10/9 = 1 1/9.
Das glaubst Du nicht? Dann machen wir einfach die Gegenprobe: 10 : 9 = 1,111... wie man durch schriftliches Dividieren leicht herausbekommt.
Ende des Einschubs zu Xenons Paradoxon. Kehren wir zurück zu unserem Babylonischen Turm. Er ist mittlerweile auf 40 Würfel gewachsen.
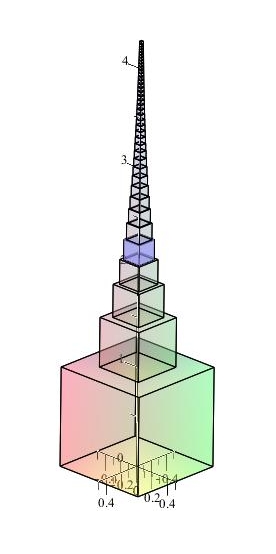
Ist er nun unendlich hoch oder nicht, anders ausgerückt:
Hat 1 + 1/2 + 1/3 + ... + 1/n + ... einen endlichen Wert oder nicht? Dann lassen wir die Katze mal aus dem Sack.
Diese unendliche Summe ist in der Mathematik das Paradebeispiel für eine unendliche Summe deren Summanden zwar immer kleiner werden, also der Null immer näher kommen, die aber doch, wie wir sehen werden, gerade noch über alle Grenzen wächst, was bedeutet, dass unser Turm am Ende unendlich hoch wird. Diese Summe wird übrigens "harmonische Reihe" genannt.
Wie kann man dies einsehen?
Um das zu verstehen, schreiben wir die Summe mal etwas ausführlicher hin und betrachten spezielle Teilsummen:
1 +
1/2 +
1/3 + 1/4 +
1/5 + 1/6 + 1/7 + 1/8 +
1/9 + 1/10 + 1/11 + 1/12 + 1/13 + 1/14 + 1/15 + 1/16 +
...
Die Idee ist folgende: wenn wir nun einzelne Summanden noch kleiner machen und die Summe mit diesen teilweise kleineren Summanden wird immer noch unendlich groß, dann wird auch die Originalsumme unendlich groß.
Wir verkleinern also ab der dritten Zeile alle Summanden bis auf den letzten gerade auf den Wert des (jeweils) letzten:
>1 +
(1/2) +
(1/4 + 1/4) +
(1/8 + 1/8 + 1/8 + 1/8) +
(1/16 + 1/16 + 1/16 + 1/16 + 1/16 + 1/16 + 1/16 + 1/16) +
...
Wie man sieht, erfolgt die Gruppierung der Summanden so, dass die Gruppen sich gerade jeweils zu 1/2 addieren:
=1 +
1/2 +
1/2 +
1/2 +
1/2 + ...
Wir nummerieren die Gruppen und zählen ihre Mitglieder.
Gruppennummer:
0 1 2 3 ...
Anzahl der Gruppenelemente:
2°=1 2 2²=4 2³=8 ...
Allerdings braucht man von Gruppe zu Gruppe doppelt so viele Summanden um den Wert 1/2 zu erreichen wie vorher, aber was soll's, die verdammte Unendlichkeit gibt's ja her!
Auf diese Weise bilden sich unendlich viele Gruppensummen der Größe 1/2 und dies führt zu einer unendlich großen Gesamtsumme. Wieso? Nun ja, jemand der behauptet, die bis ins Unendliche fortgesetzte Gesamtsumme habe einen endlichen Wert, nennen wir den mal H, dem halten wir entgegen: "Ich kann aber ausrechnen, ab welcher Gruppe die Summe größer als H wird; und wenn Du noch ein größeres H nimmst, dann wieder. Ich übertreffe dich immer!". In der Tat, ab der Gruppe mit der Nummer 2*(H - 1), ist der Wert H überschritten (der Einfachheit halber sei angenommen, H ist eine natürliche Zahl)! Also wächst die Summe über alle Grenzen und damit auch unsere harmonische Reihe (*); der Turm wird unendlich hoch.
So weit, so gut!
Alles, was wir bis jetzt erörtert haben, diente eigentlich nur der Einsicht, dass unser Turm zu Babylon unendlich hoch wird, wenn wir ihn in der beschriebenen Weise bauen. Und das wollten die Babylonier letztlich ja auch.
Befassen wir uns nun, um zum architektonischen Teil unserer Geschichte zu kommen, mit der Frage, wieviel Baumaterial für diesen Turm gebraucht würde.
Ist doch klar, unendlich viel, schließlich wird er ja unendlich hoch!
Das erscheint nahe liegend, oder?
Als erstes überlegen wir mal, wieviel Farbe benötigt würde, um die Würfel von allen Seiten anzustreichen. Jeder Würfel hat 6 Seiten, jede Seite hat eine Fläche von 1/n * 1/n = (1/n)², also müssen wir
6 * 1² + 6 * (1/2)² + 6 * (1/3)² + ... + 6*(1/n)² + ... = 6 * (1 + (1/2)² + (1/3)² + ... + (1/n)² + ...)
als Gesamtsumme berechnen.
Wieder stellt sich die Frage, ob die Summe
(1 + (1/2)² + (1/3)² + ... + (1/n)² + ...) = (1 + 1/4 + 1/9 + ... + 1/n² + ... ) (***)
einen endlichen Wert hat oder nicht.
Mit dieser Fragestellung, die unter dem Namen "Basler Problem" bekannt wurde, haben sich im 17. Jahrhundert mehrere Mathematiker, die in Basel beheimatet waren, zunächst vergeblich beschäftigt. Erst Leonhard Euler hat 1735 die Lösung gefunden.
Oh Wunder, sie hat einen endlichen Wert, wie Euler heraus fand und er konnte ihn sogar berechnen.
Die Summe von (***) beträgt pi²/6.
Also berechnet sich der Gesamtwert der Flächen unserer Würfel des Babylonischen Turmes zu pi² (= 9,8696...) und ist damit endlich.
Wir halten fest:
Obwohl der Turm eine unendliche Höhe hat, ist die Summe aller Seitenflächen seiner Bausteine endlich!
Und, wenn man so will, ist der Wert sogar "klein", aber im Vergleich zur Unendlichkeit ist jede Zahl "klein".
Nicht nur das; genauso kann man die Frage nach der Materialmenge (z.B. Beton) stellen, die man braucht, um ihn zu bauen. Auch hier kann man die Menge des Materials als unendliche Summe über die Volumina der Würfelbausteine berechnen:
1 + (1/2)³ + (1/3)³ + ... + (1/n)³ + ... = 1 + 1/8 + 1/27 + ... + 1/n³ + ...
Auch diese Summe der Volumina hat einen endlichen Wert, nämlich 1,20205 ...
Die Babylonier wurden für ihren Frevel einen so hohen Turm bauen zu wollen und damit Gott immer näher zu kommen und ihm gleich zu werden, von Gott mit der babylonischen Sprachverwirrung gestraft und zerstreuten sich, da sie sich untereinander nicht mehr verstanden in alle Windrichtungen, wird erzählt.
Und wir? Wir haben für unseren (fiktiven) Turmbau eine einheitliche Sprache benutzt, nämlich die der Mathematik; das schützt uns vor jeglicher Verwirrung, hoffe ich ...
Die Graphiken dieser Seite wurden mit dem Computeralgebraprogramm Maple erstellt.