

Der symmetrische Kreisel
Zu den schönsten Darstellungen der mechanischen Physik gehört die Visualisierung des Symmetrischen Kreisels, die ich hier unter Verwendung eines Computeralgebraprogrammes in sehr einfacher Weise animiert zeigen kann.
Die erstellten, bewegten Bilder lassen sich als "animated GIF" Dateien exportieren und werden hier so gezeigt.
Ich verwende das Programm Maple zur Darstellung; wer Interesse hat an der Quellcodedatei kann sie gerne downloaden und selber experimentieren.
Kreiselanimation als 2D Math Input
Die Bewegungen des Kreisels werden in Maple mit der Animationsfunktion simuliert, die es ermöglicht, stehende Bilder wie einen Film hintereinander ablaufen zu lassen; animated GIF tut nichts anderes.
Sämtliche Drehungen sind durch 3-dimensionale Drehmatrizen erzeugt, die durch Hintereinanderausführung (Matrixmultiplikation) auf das Grundobjekt die (überlagerten) Drehungen erzeugt.
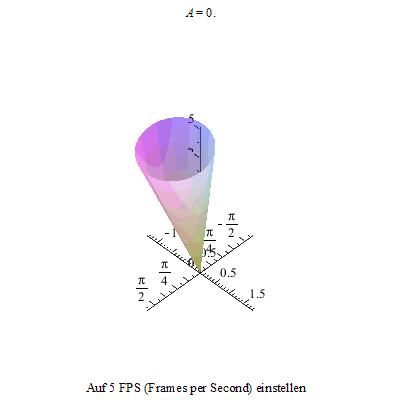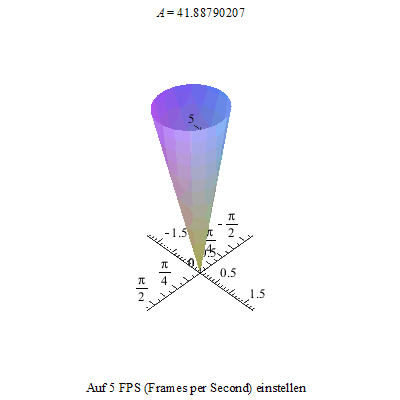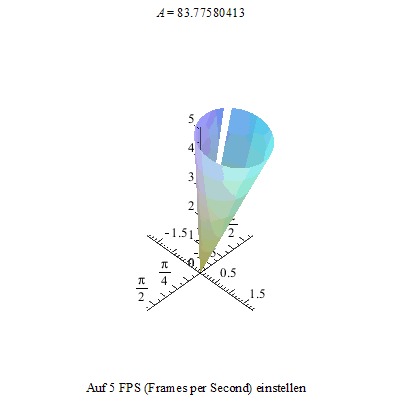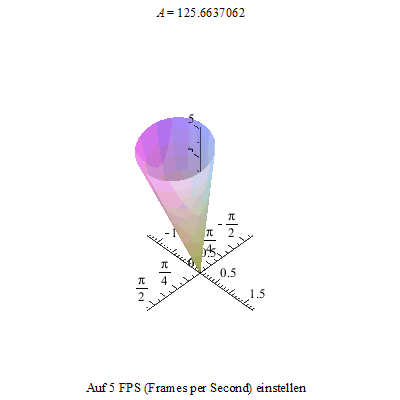
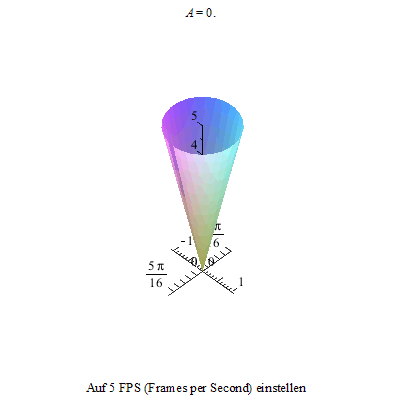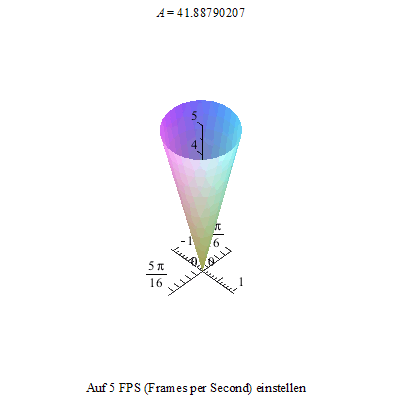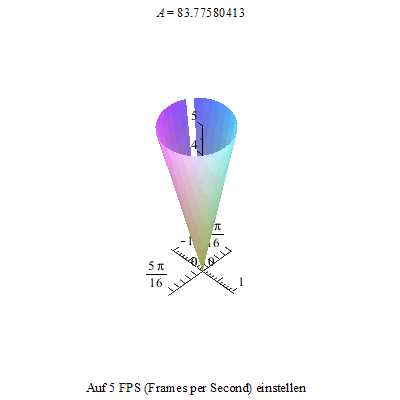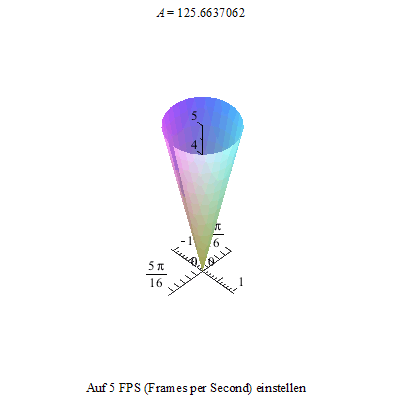
Als erstes setzen wir unseren Kreisel, hier in der Form eines auf der Spitze stehenden Kegels (Eistüte), in unser xyz - Koordinatensystem.
Die erstellten, bewegten Bilder lassen sich als "animated GIF" Dateien exportieren und werden hier so gezeigt.
Ich verwende das Programm Maple zur Darstellung; wer Interesse hat an der Quellcodedatei kann sie gerne downloaden und selber experimentieren.
Kreiselanimation als 2D Math Input
Die Bewegungen des Kreisels werden in Maple mit der Animationsfunktion simuliert, die es ermöglicht, stehende Bilder wie einen Film hintereinander ablaufen zu lassen; animated GIF tut nichts anderes.
Sämtliche Drehungen sind durch 3-dimensionale Drehmatrizen erzeugt, die durch Hintereinanderausführung (Matrixmultiplikation) auf das Grundobjekt die (überlagerten) Drehungen erzeugt.
Als erstes setzen wir unseren Kreisel, hier in der Form eines auf der Spitze stehenden Kegels (Eistüte), in unser xyz - Koordinatensystem.
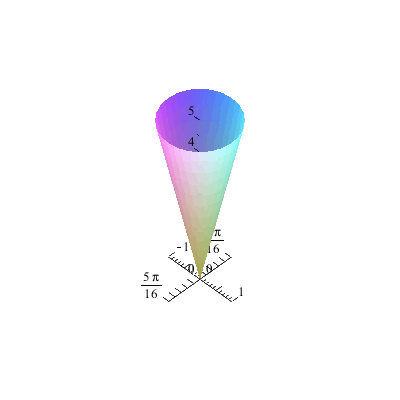
Nun lassen wir ihn rotieren und damit man das auch gut sehen kann, schneiden wir einen kleinen Spalt des Kegelmantels heraus.
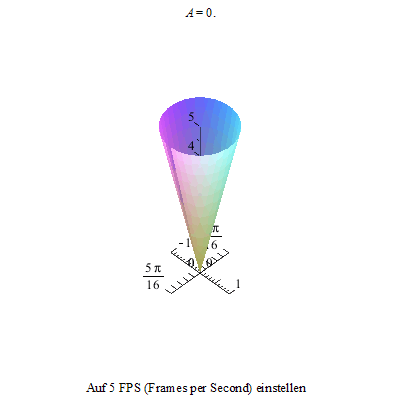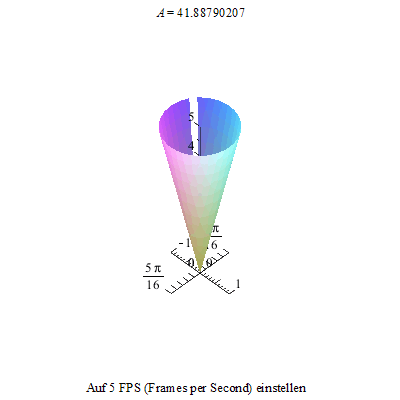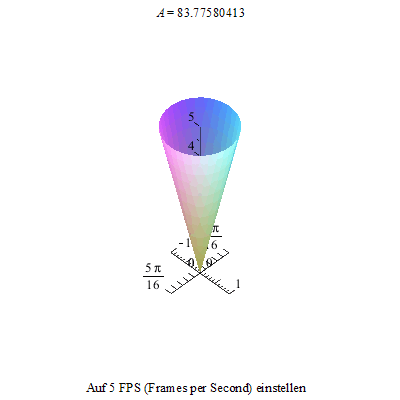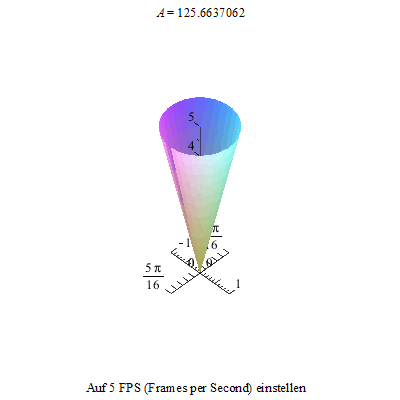
Wir kippen den Kreisel nun aus der Senkrechten in Richtung der x-Achse heraus und ...
(Dies erfolgt darstellungstechnisch ebenfalls durch eine Drehmatrix, die allerdings nicht der Animation unterworfen wird.)
(Dies erfolgt darstellungstechnisch ebenfalls durch eine Drehmatrix, die allerdings nicht der Animation unterworfen wird.)
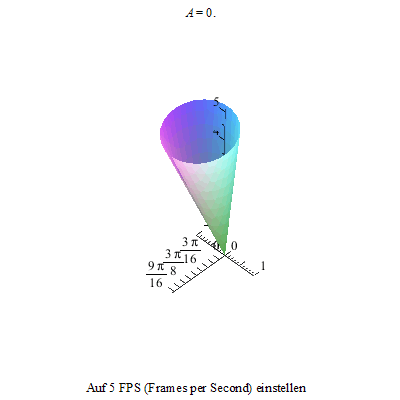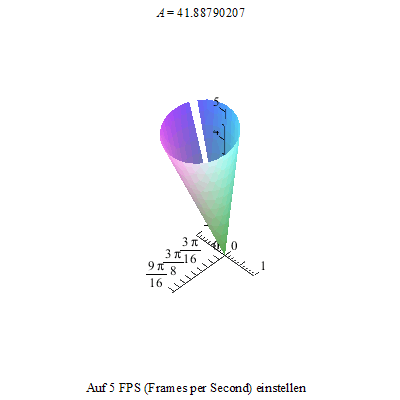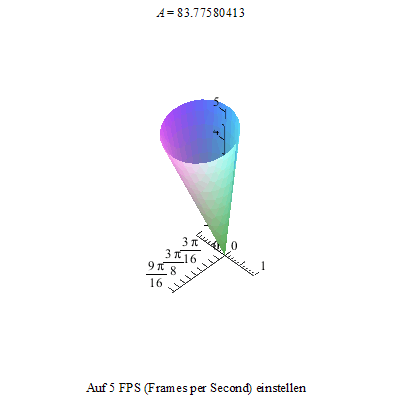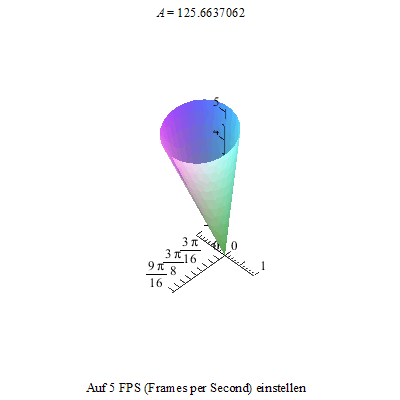
... da er nicht im Schwerpunkt gelagert ist und auch nicht als gewichtslos betrachtet wird, beginnt er zu präzessieren.
Die im Schwerpunkt angreifende, senkrecht nach unten gerichtete Schwerkraft erzeugt ein Drehmoment in dieser Richtung, das eigentlich dazu führen müsste, dass der Kreisel umfällt. Aber der physikalische Satz von der Erhaltung des Drehimpulses bewirkt, dass der Kreisel nicht umfällt, sondern eben in die präzessierende Bewegung ausweicht.
Ohne dieses physikalische Phänomen gäbe es neben vielen anderen Dingen beispielsweise keine Fahrräder, die auch nur deshalb während der Fahrt nicht umfallen, weil sich die beiden Räder ausreichend schnell drehen. Jeder Radfahrer weiss wie schwer es ist, auf einem langsamen Rad das Gleichgewicht zu halten.
Die im Schwerpunkt angreifende, senkrecht nach unten gerichtete Schwerkraft erzeugt ein Drehmoment in dieser Richtung, das eigentlich dazu führen müsste, dass der Kreisel umfällt. Aber der physikalische Satz von der Erhaltung des Drehimpulses bewirkt, dass der Kreisel nicht umfällt, sondern eben in die präzessierende Bewegung ausweicht.
Ohne dieses physikalische Phänomen gäbe es neben vielen anderen Dingen beispielsweise keine Fahrräder, die auch nur deshalb während der Fahrt nicht umfallen, weil sich die beiden Räder ausreichend schnell drehen. Jeder Radfahrer weiss wie schwer es ist, auf einem langsamen Rad das Gleichgewicht zu halten.
Außer der Drehung um die eigene Figurenachse und der Präzession gibt es noch eine dritte unabhängige Bewegung, die Nutation des Kreisels.
(Nutation kommt aus dem Lateinischen und bedeutet "Nicken", sehr einleuchtend, wenn man die Bewegung gleich sieht. Sie entsteht durch die Drehung der Figurenachse (= Rotationsachse) des Kegels um den Drehimplusvektor der Kreiseldrehung.)
(Nutation kommt aus dem Lateinischen und bedeutet "Nicken", sehr einleuchtend, wenn man die Bewegung gleich sieht. Sie entsteht durch die Drehung der Figurenachse (= Rotationsachse) des Kegels um den Drehimplusvektor der Kreiseldrehung.)
Dieses Nicken des Kreisels kann nun mit der Präzession überlagert werden. Also kippen wir den Kreisel wieder ...
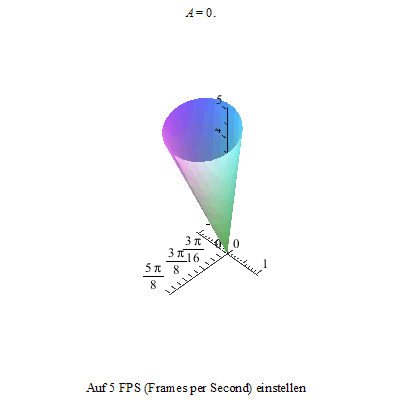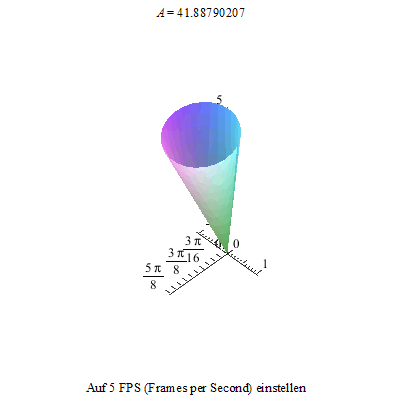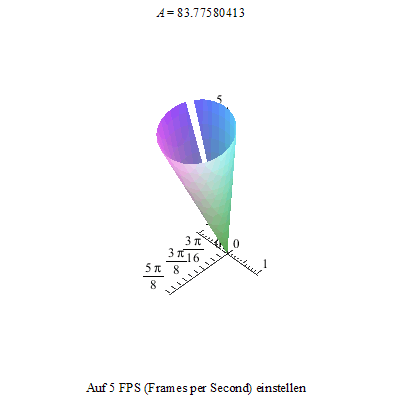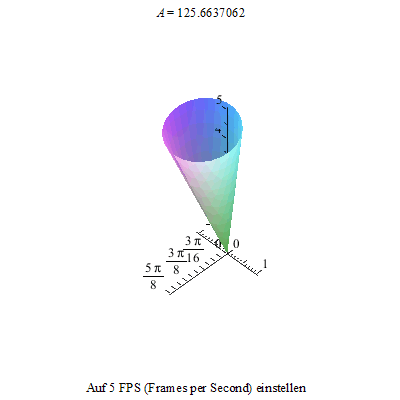
... und versetzen ihn so zusätzlich in eine Präzession.
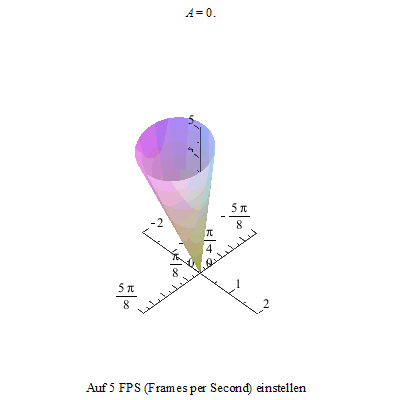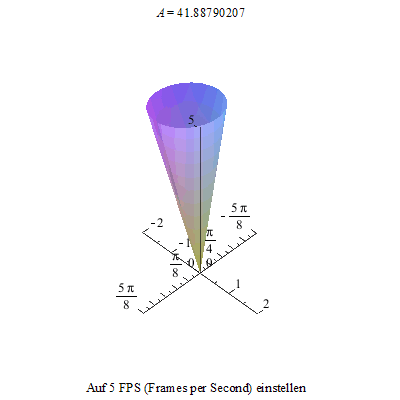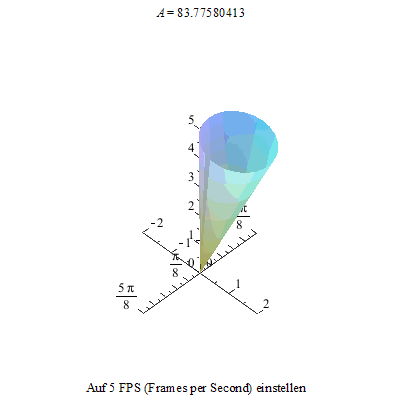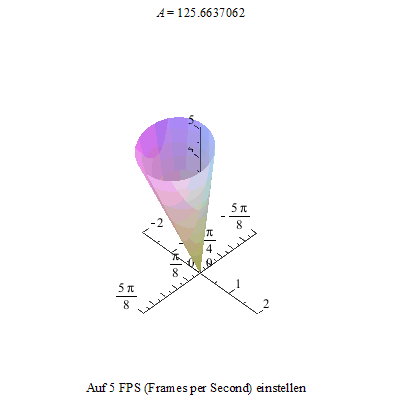
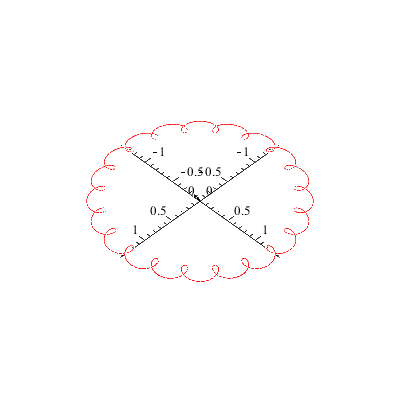
Um dieses Phänomen noch deutlicher zu machen, zeichnen wir noch die Figurenachse in rot und den Drehimpulsvektor in grün ein. Die Drehimpulsspitze bewegt sich auf einer Kreisbahn, die Figurenachse dreht sich ihrerseits um den Drehimpulsvektor und ihre Spitze beschreibt je nach der Winkelgeschwindigkeit der Nutation und der Präzession eine unterschiedlich verschlungene Kurve.
Als erstes sehen wir eine Kurve, die an ihren Maxima Schleifen bildet.
Die beiden folgenden Animationen zeigen diesen Zustand an unserem Kreisel von der Seite und von oben betrachtet.
Als erstes sehen wir eine Kurve, die an ihren Maxima Schleifen bildet.

Die beiden folgenden Animationen zeigen diesen Zustand an unserem Kreisel von der Seite und von oben betrachtet.
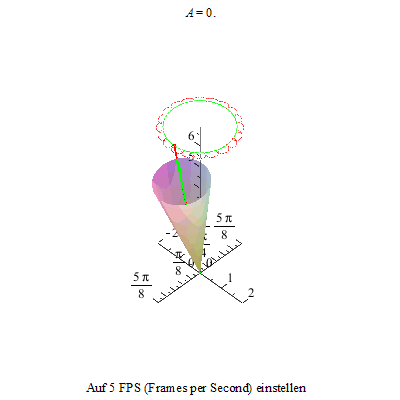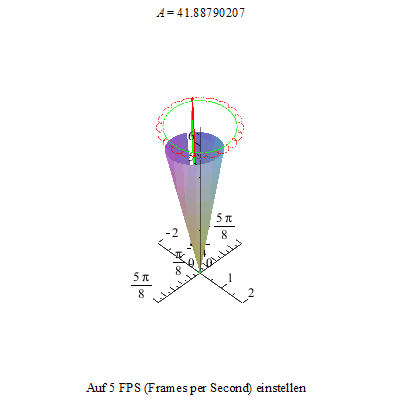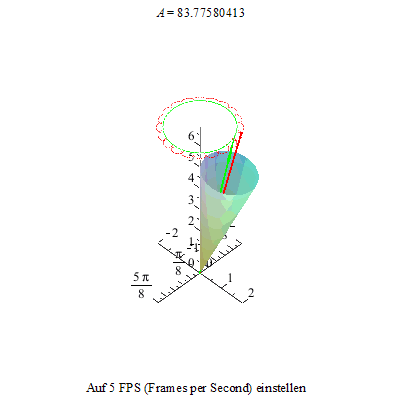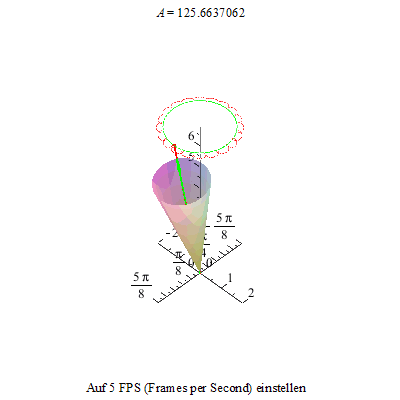
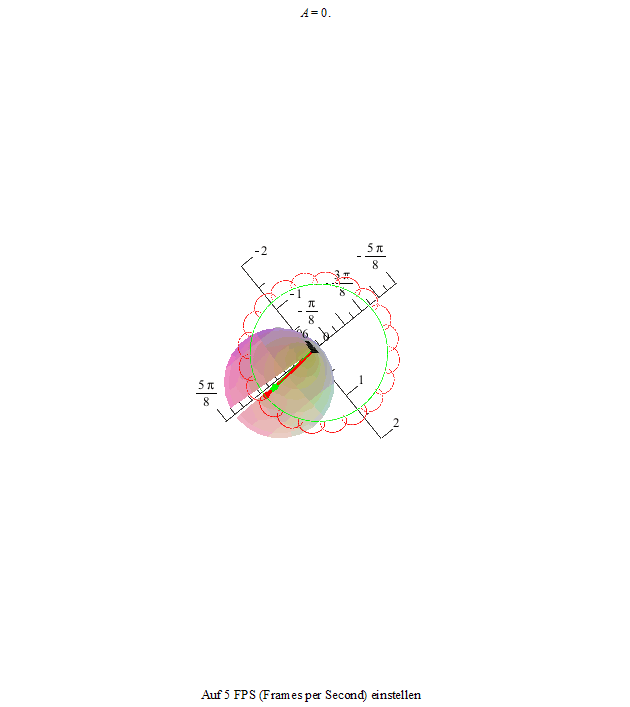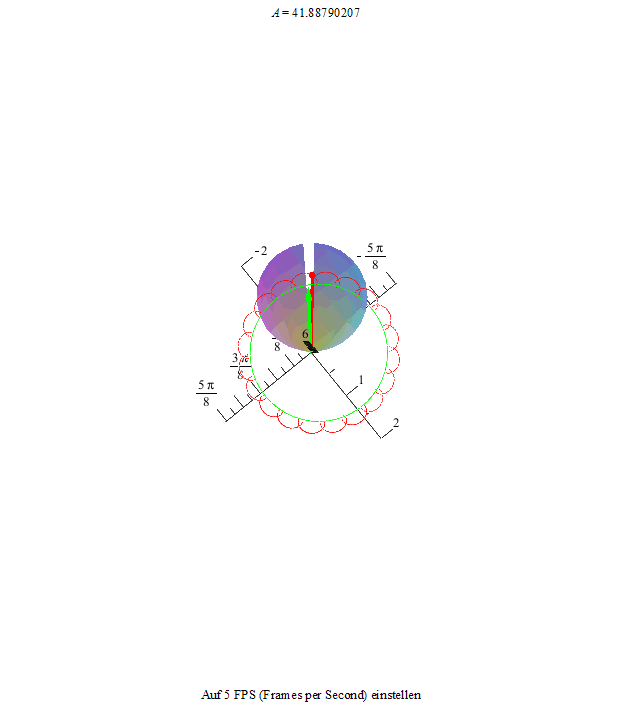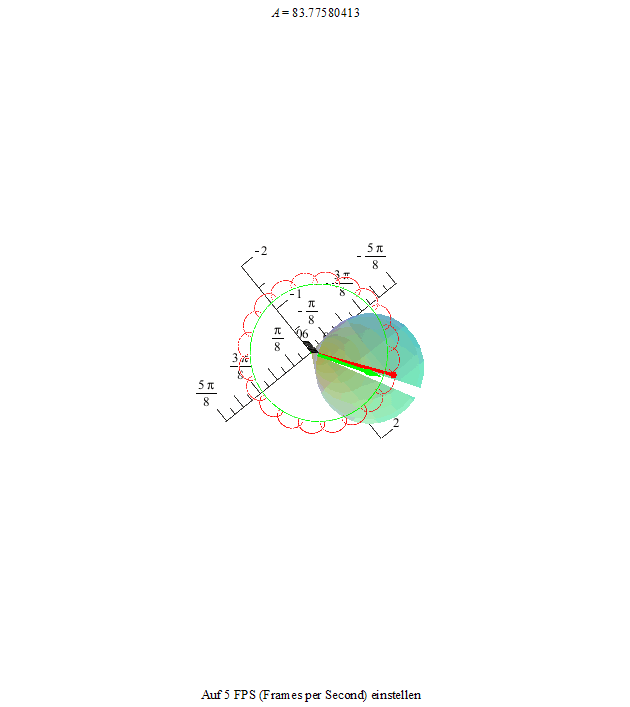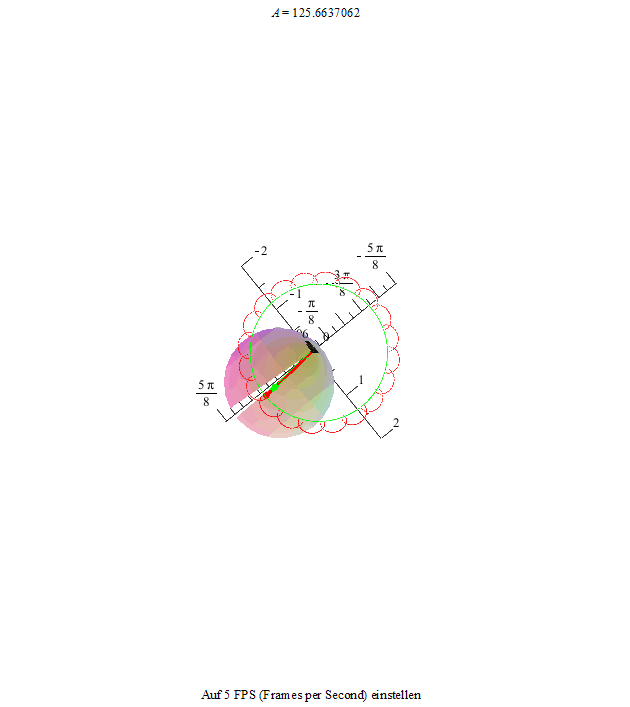
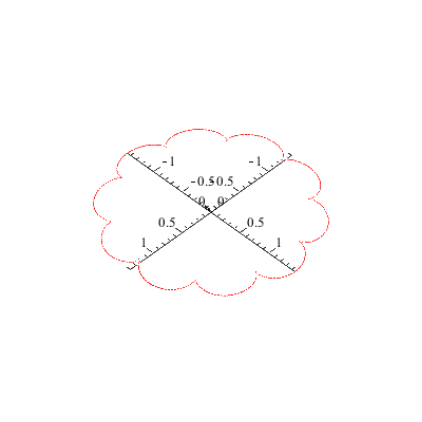
Im zweiten Bild sind die Schleifen zu Spitzen entartet:

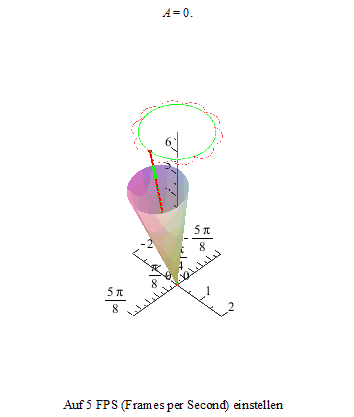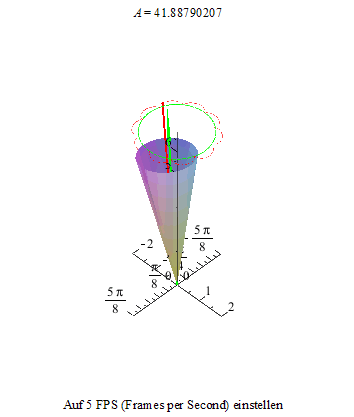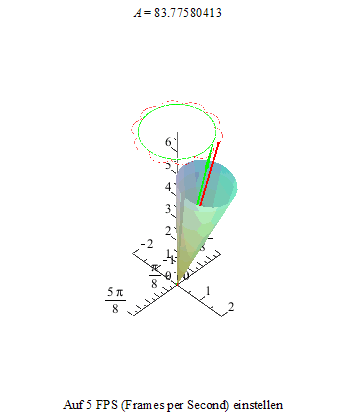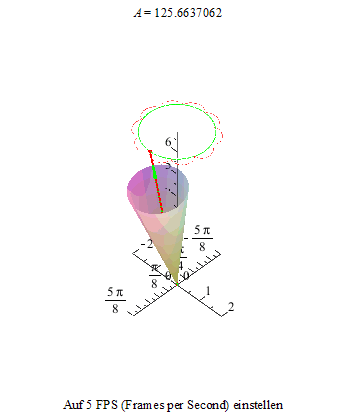
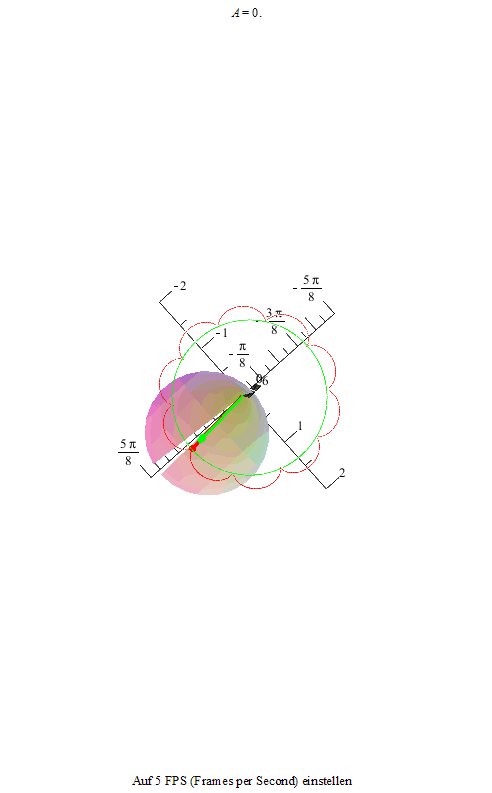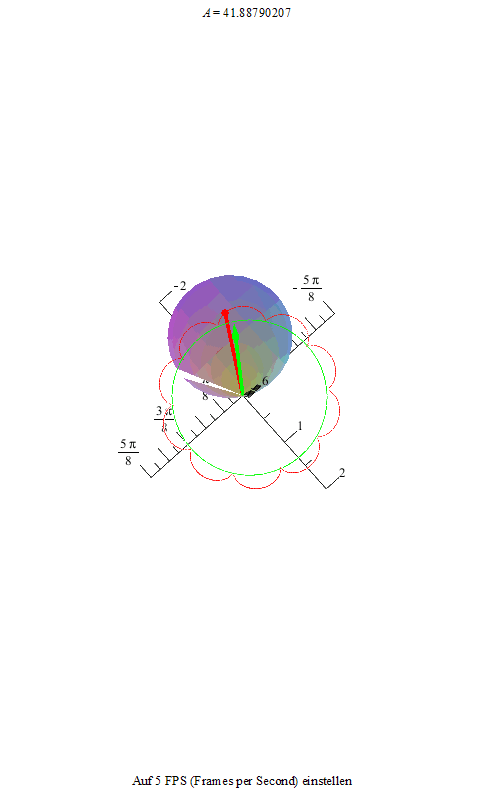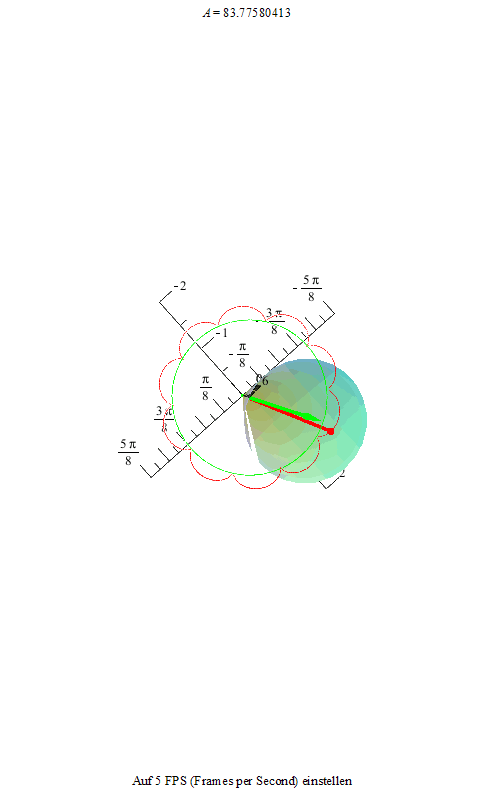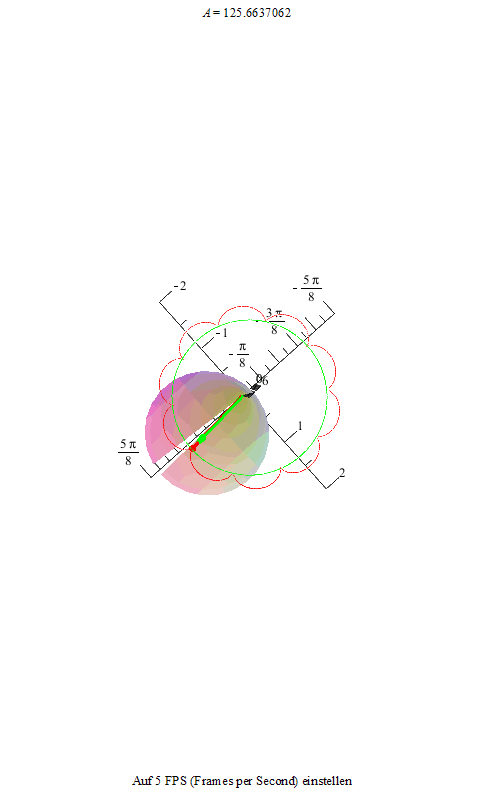
Im dritten Bild flachen die Spitzen nun zu Kurven ab:
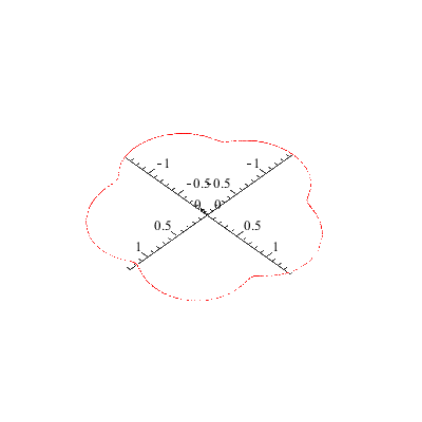



Eine filmische Darstellung dieser physikalischen Zusammenhänge findet man in einem Video der Universität Würzburg auf folgender URL.
Eine quantitativ ausgerichtete Art der Animation bietet die Seite FORCED PRECESSION OF A GYROSCOPE.
Seitenanfang
Diese Animationen wurden unter Verwendung des Computeralgebraprogrammes Maple erstellt.
Eine quantitativ ausgerichtete Art der Animation bietet die Seite FORCED PRECESSION OF A GYROSCOPE.
Seitenanfang
Diese Animationen wurden unter Verwendung des Computeralgebraprogrammes Maple erstellt.