

Bauernschach
Einleitung und Regeln
Zum ersten Mal entdeckte ich Bauernschach in einem Jugendbuch, das ich seinerzeit zu Weihnachten geschenkt bekam. Hier wurde eine 3x3 Variante des Bauernschach vorgestellt, die mir schnell langweilig wurde.
Erst vor einigen Jahren wurde ich durch einen Internetartikel auf dieses Spiel erneut aufmerksam und ich begann, mir Gedanken über Spielstrategien und Spielvarianten zu machen. Bevor ich über meine Überlegungen und Ergebnisse berichte, sollte ich zunächst mal erklären, was Bauernschach eigentlich ist.
Einfach ausgedrückt ist Bauernschach eine simple Variante des Schach, die nur mit Bauern gespielt wird. Die Variationen ergeben sich zunächst aus der Größe des Brettes (3x3, 4x4, 5x5 usw.) und zwei möglichen Zusatzregeln, die aus dem Schach bekannt sind, nämlich der Doppelschritt eines Bauern von der Grundlinie aus und dem Schlagen im Vorbeigehen (i.V.).
Aber erst mal für Anfänger: Ein Schachbrett aus n x n Feldern, wir beginnen mit 3 x 3, hat in der Grundstellung auf einer Seite weiße Spielfiguren (Bauern), auf der anderen schwarze.
Beispiel für eine Grundstellung eines 3 x 3 Brettes.
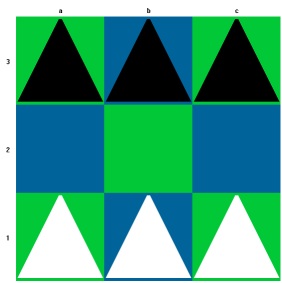
Die Bauern sind hier als Dreiecke dargestellt. Um die Felder des Brettes eindeutig benennen zu können, bezeichnet man die Zeilen des Brettes mit Nummern (hier 1 bis 3) und die Spalten mit Buchstaben (hier a bis c). Das Feld in der Mitte hat somit die Bezeichnung b2, das Feld rechts oben heißt c3.
Die zwei Spieler machen nun abwechselnd einen Zug, wobei Weiß beginnt. Es gibt zwei erlaubte Sorten von Zügen: Ziehen oder Schlagen. Ziehen kann ein Bauer indem er ein Feld in Richtung der gegnerischen Grundlinie (das sind die Felder auf denen anfangs die gegnerischen Bauern stehen) geht, aber nur sofern dieses Feld frei ist (also nicht von einem eigenen oder gegnerischen Bauern besetzt ist).
Beispiele für zulässige Züge:
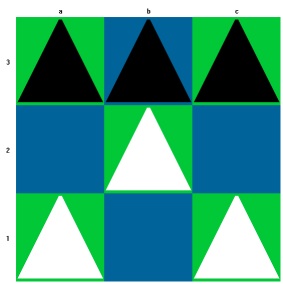

Um genau zu sein, besteht ein Schachzug aus zwei Halbzügen, einem Weißen und einem Schwarzen.
Schlagen kann ein Bauer in Richtung der gegnerischen Grundlinie durch schräges Voranschreiten (links oder rechts), aber nur auf ein Feld, auf dem ein gegnerischer Bauer steht.
Beispiel:

Ziel des Spieles ist es, einen Bauern auf die generische Grundlinie zu platzieren; wenn das gelingt, wie in obigem Beispiel, ist das Spiel sofort zu Ende und die Farbe, die das erreicht hat, hat gewonnen.
Ein Spiel kann aber auch unentschieden ausgehen (nennt man remis), nämlich dann, wenn die Farbe, die am Zug ist, nicht mehr ziehen kann (auch dann, wenn ein Spieler überhaupt keine Figur mehr hat).
Beispiele für unentschiedene Stellungen:
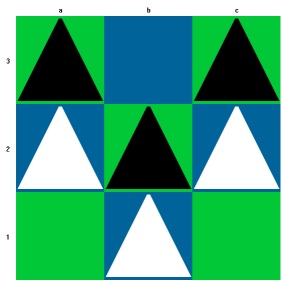


Auf die oben genannten Sonderregeln gehe ich später noch ein. Zunächst eine Partie als weitere Illustration des Spiels:
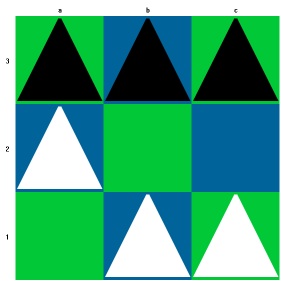
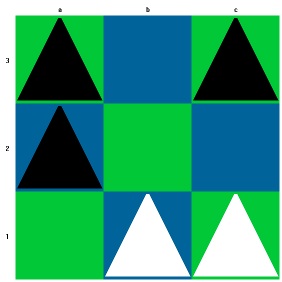
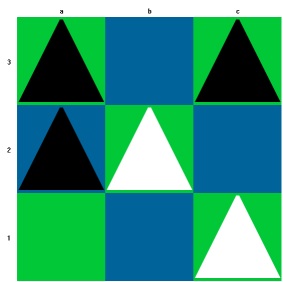

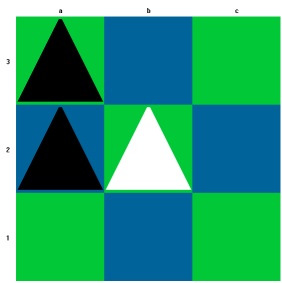

Und Schwarz gewinnt.
Nun zu den beiden Sonderregeln:
1. Doppelschritt von der Grundlinie aus
Wie auch beim normalen Schach kann man als Sonderregel den Doppelschritt von der Grundlinie aus zulassen. Dies ist aber beim 3 x 3 - Brett eine etwas absonderlich anmutende Regel, denn mit ihr kann der jeweilige Bauer sofort auf die gegnerische Grundlinie gezogen werden und damit gewinnen; aber die Regel ist trotzdem anwendbar und hat, wie wir später sehen werden, auf dem 3 x 3 - Brett eine revolutionäre Auswirkung.
Sehen wir uns dazu ein Beispiel an:
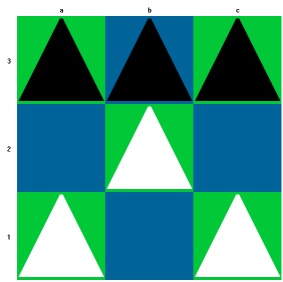
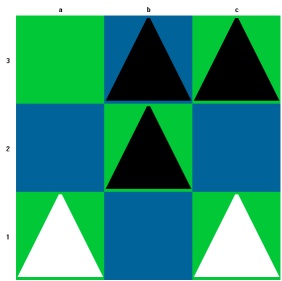
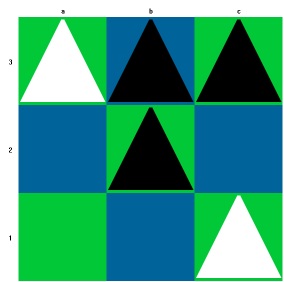
Weiß gewinnt durch einen Doppelschritt von der Grundlinie aus auf die gegnerische Grundlinie.
2. Schlagen im Vorbeigehen
Diese Sonderregel setzt den Doppelschritt voraus, denn sie ist nur unmittelbar nach einem Doppelschritt anwendbar; landet der Doppelschritt auf einem Feld neben einem gegnerischen Bauern, so kann dieser schlagen, als ob der Doppelschritt-Bauer nur einen Einzelschritt von der Grundlinie gemacht hätte. Das Schlagen muss aber unmittelbar nach dem Doppelschritt erfolgen und nicht zu einem späteren Zeitpunkt. Natürlich ist dieser Zug nicht auf einem 3 x 3 - Brett ausführbar; wie wir sahen ist das Spiel auf einem 3 x 3 - Brett nach einem Doppelschritt beendet. Nun ein Beispiel für ein Schlagen i.V.:

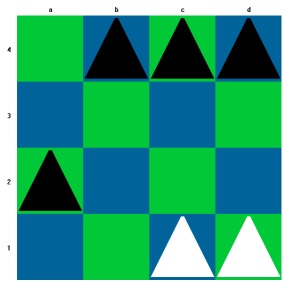
Der weiße Bauer hat einen Dopelschritt von der Grundlinie aus gemacht (a1 - a3) und steht neben dem schwarzen Bauern auf b3. Dieser kann jetzt Schlagen i.V. (b3 - a2).
Soweit die einfachen Regeln des Bauernschach.
In den folgenden Kapiteln zeige ich die selbst gestellten Aufgaben und die erzielten Ergebnisse. In weiteren Versionen dieser Webseite wird das benutzte Analyseprogramm erläutert und das Programm zum Spielen veröffentlicht.
Ich danke an dieser Stelle meiner Frau für ihre hilfreiche Unterstützung durch ein Vielzahl von Gesprächen und Hinweisen und daraus erwachsenden Lösungsansätzen.
Erst vor einigen Jahren wurde ich durch einen Internetartikel auf dieses Spiel erneut aufmerksam und ich begann, mir Gedanken über Spielstrategien und Spielvarianten zu machen. Bevor ich über meine Überlegungen und Ergebnisse berichte, sollte ich zunächst mal erklären, was Bauernschach eigentlich ist.
Einfach ausgedrückt ist Bauernschach eine simple Variante des Schach, die nur mit Bauern gespielt wird. Die Variationen ergeben sich zunächst aus der Größe des Brettes (3x3, 4x4, 5x5 usw.) und zwei möglichen Zusatzregeln, die aus dem Schach bekannt sind, nämlich der Doppelschritt eines Bauern von der Grundlinie aus und dem Schlagen im Vorbeigehen (i.V.).
Aber erst mal für Anfänger: Ein Schachbrett aus n x n Feldern, wir beginnen mit 3 x 3, hat in der Grundstellung auf einer Seite weiße Spielfiguren (Bauern), auf der anderen schwarze.
Beispiel für eine Grundstellung eines 3 x 3 Brettes.

Die Bauern sind hier als Dreiecke dargestellt. Um die Felder des Brettes eindeutig benennen zu können, bezeichnet man die Zeilen des Brettes mit Nummern (hier 1 bis 3) und die Spalten mit Buchstaben (hier a bis c). Das Feld in der Mitte hat somit die Bezeichnung b2, das Feld rechts oben heißt c3.
Die zwei Spieler machen nun abwechselnd einen Zug, wobei Weiß beginnt. Es gibt zwei erlaubte Sorten von Zügen: Ziehen oder Schlagen. Ziehen kann ein Bauer indem er ein Feld in Richtung der gegnerischen Grundlinie (das sind die Felder auf denen anfangs die gegnerischen Bauern stehen) geht, aber nur sofern dieses Feld frei ist (also nicht von einem eigenen oder gegnerischen Bauern besetzt ist).
Beispiele für zulässige Züge:


Weiß zieht von b1 nach b2, Schwarz im Gegenzug von a3 nach a2.
Um genau zu sein, besteht ein Schachzug aus zwei Halbzügen, einem Weißen und einem Schwarzen.
Schlagen kann ein Bauer in Richtung der gegnerischen Grundlinie durch schräges Voranschreiten (links oder rechts), aber nur auf ein Feld, auf dem ein gegnerischer Bauer steht.
Beispiel:

Hier hat Weiß einen schwarzen Bauern geschlagen von b2 nach c3.
Ziel des Spieles ist es, einen Bauern auf die generische Grundlinie zu platzieren; wenn das gelingt, wie in obigem Beispiel, ist das Spiel sofort zu Ende und die Farbe, die das erreicht hat, hat gewonnen.
Ein Spiel kann aber auch unentschieden ausgehen (nennt man remis), nämlich dann, wenn die Farbe, die am Zug ist, nicht mehr ziehen kann (auch dann, wenn ein Spieler überhaupt keine Figur mehr hat).
Beispiele für unentschiedene Stellungen:









Und Schwarz gewinnt.
Nun zu den beiden Sonderregeln:
1. Doppelschritt von der Grundlinie aus
Wie auch beim normalen Schach kann man als Sonderregel den Doppelschritt von der Grundlinie aus zulassen. Dies ist aber beim 3 x 3 - Brett eine etwas absonderlich anmutende Regel, denn mit ihr kann der jeweilige Bauer sofort auf die gegnerische Grundlinie gezogen werden und damit gewinnen; aber die Regel ist trotzdem anwendbar und hat, wie wir später sehen werden, auf dem 3 x 3 - Brett eine revolutionäre Auswirkung.
Sehen wir uns dazu ein Beispiel an:



Weiß gewinnt durch einen Doppelschritt von der Grundlinie aus auf die gegnerische Grundlinie.
2. Schlagen im Vorbeigehen
Diese Sonderregel setzt den Doppelschritt voraus, denn sie ist nur unmittelbar nach einem Doppelschritt anwendbar; landet der Doppelschritt auf einem Feld neben einem gegnerischen Bauern, so kann dieser schlagen, als ob der Doppelschritt-Bauer nur einen Einzelschritt von der Grundlinie gemacht hätte. Das Schlagen muss aber unmittelbar nach dem Doppelschritt erfolgen und nicht zu einem späteren Zeitpunkt. Natürlich ist dieser Zug nicht auf einem 3 x 3 - Brett ausführbar; wie wir sahen ist das Spiel auf einem 3 x 3 - Brett nach einem Doppelschritt beendet. Nun ein Beispiel für ein Schlagen i.V.:


Der weiße Bauer hat einen Dopelschritt von der Grundlinie aus gemacht (a1 - a3) und steht neben dem schwarzen Bauern auf b3. Dieser kann jetzt Schlagen i.V. (b3 - a2).
Soweit die einfachen Regeln des Bauernschach.
In den folgenden Kapiteln zeige ich die selbst gestellten Aufgaben und die erzielten Ergebnisse. In weiteren Versionen dieser Webseite wird das benutzte Analyseprogramm erläutert und das Programm zum Spielen veröffentlicht.
Ich danke an dieser Stelle meiner Frau für ihre hilfreiche Unterstützung durch ein Vielzahl von Gesprächen und Hinweisen und daraus erwachsenden Lösungsansätzen.
Fragen und Antworten
Zwei Aufgaben habe ich mir im Zusammenhang mit Bauernschach gestellt:
Am Anfang habe ich zwischen den beiden Aufgabenstellungen keinen engeren Zusammenhang gesehen, aber nach der Analysephase wurde sehr deutlich, dass die Ergebnisse des ersten Teils wesentliche Grundlage für die zweite Aufgabe sein würden.
Auf dieser Seite möchte ich die Fragestellungen und die erzielten Ergebnisse zusammengefasst darstellen und meine Vorgehensweise motivieren, ohne auf die benutzten Methoden vertieft einzugehen; dies geschieht dann in einem separaten Anhang für interessierte Leser.
Von den oben genannten Aufgabenstellungen habe ich nicht nur die zweite, sondern auch die erste durch Entwicklung eines Computerprogrammes in der Sprache Pascal (genauer FPC) unter heftiger Ausnutzung der mitgelieferten Unterprogrammbibliotheken gelöst.
1. Aufgabe - Erstellen eines vollständigen Spielbaumes
Komplexe Spiele wie beispielsweise Schach erlauben es nicht, sämtliche möglichen Stellungen und alle Züge komplett zu katalogisieren um beispielsweise die Frage zu beantworten, wer bei optimaler Strategie gewinnt bzw. ob es überhaupt eine solche gibt. Die Züge des 3 x 3 - Brettes beim Bauernschach sind aber so überschaubar, dass hier eine komplette Auflistung noch im Bereich des Möglichen liegt, zunächst mal abgesehen von der Frage, was dies dann für einen Nährwert hat (später mehr dazu). Eine sehr grobe erste Abschätzung der Anzahl der maximal möglichen Spielstellungen liefert die Überlegung, dass ein Spielfeld von n x n Feldern, die jeweils 3 Zustände annehmen können (Weiss, Schwarz, leer), maximal 3**(n**2) verschiedenen Stellungen haben kann; für n = 3 sind dies also 19683 Stellungen, von denen die meisten allerdings unmöglich sind und im Spiel nicht vorkommen. Man erhält dieses Ergebnis, indem man sich die n**2 Felder des Spielbrettes als mit einer Zahl im Dreiersystem (3 mögliche Zustände jedes Feldes) belegt vorstellt.
Somit begann ich in meinem Programm "Bauern" unter Entwicklung eines rekursiven Algorithmus, den Spielbaum (zunächst aller möglicher Halbzüge = Kanten des Baumes und Stellungen = Knoten des Baumes) komplett aufzubauen und als Ergebnis auszugeben. Das Programm habe ich von vorne herein so angelegt, dass durch Ändern der Seitenlänge des Brettes auch größere Schachbretter ohne weitere Programmänderung untersucht werden können (zumindest theoretisch).
Sehr schnell erkannte ich, dass ein Großteil der vorkommenden Stellungen an vielen Knoten des Baumes mehrfach auftrat und damit natürlich auch alle darunter liegenden Halbzüge, was den Baum unnötig aufblähte. Die erste Verbesserung bestand also darin, mehrfach vorkommende Zweige des Baumes nicht mehrfach auszugeben, sondern bei einer "Doublette" einen Verweis auf das erste Vorkommen der Stellung zu notieren; dazu wurden die Stellungen durchnummeriert. Letztlich wurde der Baum dadurch zum gerichteten Graphen. Das Wiedererkennen einer schon vorhandenen Stellung erfolgt über eine Hashtabelle, die alle vorkommenden Stellungen und die dazu gehörigen Positionen im Graphen enthält.
Beim Aufbau des Stellungsgraphen werden parallel statistische Werte ermittelt, die die Komplexität des Problems beschreiben; darüber hinaus tragen sie zur Verifikation der Korrektheit des Programmes dar.
Die folgende Datei enthält das Ergebnis für das 3 x 3 - Brett.
Ausgabe_3x3.txt
Zur Erläuterung hier zwei Ausschnitte aus dieser Datei:
1.S.0.1
S S S
0 0 0
W W W
2.W.1.1 <----laufende Nummer der Stellung.Farbe, die gezogen hat.Baumtiefe.Position in der Warteliste
S S S
W 0 0
0 W W
3.S.2.1
S 0 S
W S 0
0 W W
4.W.3.1
S 0 S
W S W
0 W 0
S kann nicht mehr ziehen <---- unentschiedener Ausgang in diesem Zweig
5.W.3.2
S 0 S
W W 0
0 W 0
6.S.4.1
0 0 S
W S 0
0 W 0
7.W.5.1
W 0 S
0 S 0
0 W 0
W hat gewonnen <----- Gewinnstellung für Weiß
8.S.4.2
S 0 0
W W S
0 W 0
9.W.5.1
S W 0
W 0 S
0 W 0
W hat gewonnen
.
.
.
Der Aufbau des Stellungsgraphen beginnt natürlich bei der Grundstellung und schreitet von links nach rechts voran, d.h. die möglichen weißen Züge in dieser und allgemein jeder Stellung, in der Weiß am Zug ist, werden immer mit dem weißen Bauern geführt, der am weitesten links steht; gleiches gilt für die schwarzen Bauern. Zuerst wird versucht zu ziehen, dann nach links zu schlagen, dann nach rechts.
Bei jedem Halbzug wird die Stellungsanzeige ein Stück nach rechts gerückt; dies korrespondiert zu der Ziffer, die ich "Baumtiefe" genannt habe (Baumtiefe beginnt in der Grundstellung bei 0). Landet der Zweig aber an einem Endpunkt (Unentschieden oder Gewinn) wird auf der gleichen Baumtiefe mit dem nächsten möglichen Zug der gleichen Farbe fortgefahren. Hier nun wird die vierte Ausgabe, genannt "Position in der Warteliste" inkrementiert. Siehe dazu die Halbzüge mit den Nummern 3, 4 und 5. Ist die Warteliste leer, d.h. gibt es keinen weiteren Zug, reduziert sich die Baumtiefe bis zu der Posititon in der wieder ein Zug möglich ist (siehe Übergang von Halbzug 7 nach 8).
Der zweite Ausschnitt zeigt nun den Fall einer Doublette:
.
.
.
27.S.6.3
0 0 0
S S 0
0 0 0
W kann nicht mehr ziehen
28.S.4.3
S 0 0
S W S
0 0 W
29.W.5.1
S W 0
S 0 S
0 0 W
W hat gewonnen
30.W.5.2
W 0 0
S 0 S
0 0 W
W hat gewonnen
31.S.4.4
S 0 0
S S 0
0 0 W
32.W.5.1
S 0 0
S S W
0 0 0
33.S.6.1
S 0 0
0 S W
S 0 0
S hat gewonnen
34.S.6.2
S 0 0
S 0 W
0 S 0
S hat gewonnen
35.W.5.2
S 0 0
S W 0
0 0 0
36.S.6.1
S 0 0
0 W 0
S 0 0
S hat gewonnen
S0975812 000SS0000 Doublette Original: 27
37.W.3.2
S 0 S
W 0 0
0 0 W
.
.
.
Hier taucht zwischen dem 36. und 37. Halbzug eine schon einmal vorgekommenen Stellung auf, nämlich die mit der Nummer 27. Sie entsteht als zweite Position hinter dem Halbzug 35 und hätte eigentlich die Halbzugnummer 37. Im Falle von Dubletten wird aber der gesamte dahinter hängende Zweig ausgeblendet und auch in der Nummerierung der Halbzüge ignoriert. Man beachte, dass Doublette nicht nur Stellungsgleichheit bedeutet, sondern nur vorliegt, wenn auch die gleiche Farbe am Zug ist.
Am Ende der Datei folgen die eigentlich interessanten zusammenfassenden Ergebnisse der Analyse des Stellungsgraphen.
Anzahl Stellungen ohne Doubletten: 135
Anzahl Stellungen incl. Doubletten: 252
weisse Gewinne 58 schwarze Gewinne 50
unentschieden 26 maxtiefe: 7
maximale Laenge der Warteliste: 4
Anzahl der moeglichen Stellungen: 19683
Anzahl gefundener Doubletten: 117
Wie man sieht, gibt es fast so viele Doubletten wie Stellungen ohne Doubletten. Die Anzahl der Gewinnstellungen scheint eine höhere Gewinnchance für Weiß zu suggerieren; wie wir sehen werden ist diese Vermutung im Sinne einer optimalen Strategie aber grundfalsch.
Die Baumtiefe nimmt maximal den Wert 7 an und in der Warteliste stehen maximal 4 Elemente. Die Zählung der drei Ergebnistypen erfolgte inklusive der jeweiligen Doublettenzweige.
2. Aufgabe Gewinnstrategie, der Min - Max - Algorithmus
In der Mathematik gibt es ein Teilgebiet mit dem Namen Spieltheorie. Die Ergebnisse dieser Theorie machen Aussagen über den Ausgang und den Verlauf von Spielen. Der von John Forbes Nash entwickelte Min - Max - Algorithmus liefert Ergebnisse so genannter "2-Personen-Nullsummenspielen mit vollständiger Information". Bauernschach (wie auch Schach und andere Spiele) ist ein solches Spiel und der Min - Max lässt sich darauf anwenden. Die Grundidee ist die Bewertung jeder einzelnen Stellung nach den drei Kriterien "Weiß wird gewinnen", "Schwarz wird gewinnen" und "wird unentschieden ausgehen", wenn eine optimale Strategie angewendet wird; wir kürzen diese möglichen Ausgänge mit 1, -1 und 0 ab.
Dummerweise sieht man erst am Ende eines jeden Zweiges im Stellungsbaum, wie der Ausgang des Spieles an dieser Stelle ist, was bedeutet, dass nur bei genauer Kenntnis des Baumes eine genaue Vorhersage des Spielausganges möglich ist. Wie wird der Algorithmus nun angewendet? Nehmen wir an, der Spielbaum wäre komplett bestimmt. An jedem Ende eines Zweiges dieses Baumes bewertet man den Spielausgang mit 1, -1 oder 0 (da kennt man ja das Ergebnis) und verfolgt nun den Zweig zurück und bewertet alle Stellungen mit dem gleichen Wert bis zwei oder mehr Zweige zusammentreffen. Die dortige Stellung bekommt nun als Bewertung, und daher der Name des Algorithmus, das Maximum (oder das Minimum) der letzten Bewertungen bevor die Zweige aufeinandertreffen. Man nimmt das Maximum, wenn man eine Stellung bewertet, die einen Halbzug für Weiß beschreibt, entsprechend das Minimum, wenn ein Halbzug für Schwarz dran ist.
Folgender Ausschnitt aus der Visualisierung eines Spielbaumes zeigt die Anwendung des Algorithmus:
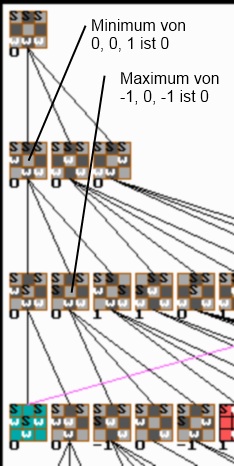
In der obigen Grafik sind die Bewertungen des Min - Max - Algorithmus an der linken unteren Ecke des Schachbrettes angezeigt. Die Bewertung der Startaufstellung zeigt letztlich das gewünschte Ergebnis: Bei optimaler Strategie kann Weiß als Startspieler höchstens ein Unentschieden erreichen. Aber auch die darunter liegenden Ebenen des Baumes zeigen relevante Zwischenergebnisse, z.B. zeigt die zweite Ebene, dass auch Schwarz unabhängig vom weissen Anfangszug ein Unentschieden erreichen kann, wenn es optimal spielt.
Die obige Grafik stellt das Ergebnis des 3 x 3 - Brettes ohne Doppelschritt dar.
Programmtechnisch wurde der Min - Max - Algorithmus bereits beim Aufbau des Stellungsgraphen angewendet und seine Ergebnisse in den Knoten des Graphen mit abgespeichert. Somit konnte die Ausgabe des Ergebnisses am Ende der jeweiligen Ausgabedatei bereits angezeigt werden:
Ergebnis des MinMax - Algorithmus: 0 <----- Wert für Weiß in der Grundstellung
0 0 0 <----- Werte für Schwarz im ersten Gegen(halb-)zug
- Analyse des Spieles nach verschiedenen Kriterien wie Komplexität, Gewinnstrategie aber auch Darstellung der Brettstellungen als Baumstruktur
- Erstellung eines Spielprogrammes zum Spiel gegen den Computer
Am Anfang habe ich zwischen den beiden Aufgabenstellungen keinen engeren Zusammenhang gesehen, aber nach der Analysephase wurde sehr deutlich, dass die Ergebnisse des ersten Teils wesentliche Grundlage für die zweite Aufgabe sein würden.
Auf dieser Seite möchte ich die Fragestellungen und die erzielten Ergebnisse zusammengefasst darstellen und meine Vorgehensweise motivieren, ohne auf die benutzten Methoden vertieft einzugehen; dies geschieht dann in einem separaten Anhang für interessierte Leser.
Von den oben genannten Aufgabenstellungen habe ich nicht nur die zweite, sondern auch die erste durch Entwicklung eines Computerprogrammes in der Sprache Pascal (genauer FPC) unter heftiger Ausnutzung der mitgelieferten Unterprogrammbibliotheken gelöst.
1. Aufgabe - Erstellen eines vollständigen Spielbaumes
Komplexe Spiele wie beispielsweise Schach erlauben es nicht, sämtliche möglichen Stellungen und alle Züge komplett zu katalogisieren um beispielsweise die Frage zu beantworten, wer bei optimaler Strategie gewinnt bzw. ob es überhaupt eine solche gibt. Die Züge des 3 x 3 - Brettes beim Bauernschach sind aber so überschaubar, dass hier eine komplette Auflistung noch im Bereich des Möglichen liegt, zunächst mal abgesehen von der Frage, was dies dann für einen Nährwert hat (später mehr dazu). Eine sehr grobe erste Abschätzung der Anzahl der maximal möglichen Spielstellungen liefert die Überlegung, dass ein Spielfeld von n x n Feldern, die jeweils 3 Zustände annehmen können (Weiss, Schwarz, leer), maximal 3**(n**2) verschiedenen Stellungen haben kann; für n = 3 sind dies also 19683 Stellungen, von denen die meisten allerdings unmöglich sind und im Spiel nicht vorkommen. Man erhält dieses Ergebnis, indem man sich die n**2 Felder des Spielbrettes als mit einer Zahl im Dreiersystem (3 mögliche Zustände jedes Feldes) belegt vorstellt.
Somit begann ich in meinem Programm "Bauern" unter Entwicklung eines rekursiven Algorithmus, den Spielbaum (zunächst aller möglicher Halbzüge = Kanten des Baumes und Stellungen = Knoten des Baumes) komplett aufzubauen und als Ergebnis auszugeben. Das Programm habe ich von vorne herein so angelegt, dass durch Ändern der Seitenlänge des Brettes auch größere Schachbretter ohne weitere Programmänderung untersucht werden können (zumindest theoretisch).
Sehr schnell erkannte ich, dass ein Großteil der vorkommenden Stellungen an vielen Knoten des Baumes mehrfach auftrat und damit natürlich auch alle darunter liegenden Halbzüge, was den Baum unnötig aufblähte. Die erste Verbesserung bestand also darin, mehrfach vorkommende Zweige des Baumes nicht mehrfach auszugeben, sondern bei einer "Doublette" einen Verweis auf das erste Vorkommen der Stellung zu notieren; dazu wurden die Stellungen durchnummeriert. Letztlich wurde der Baum dadurch zum gerichteten Graphen. Das Wiedererkennen einer schon vorhandenen Stellung erfolgt über eine Hashtabelle, die alle vorkommenden Stellungen und die dazu gehörigen Positionen im Graphen enthält.
Beim Aufbau des Stellungsgraphen werden parallel statistische Werte ermittelt, die die Komplexität des Problems beschreiben; darüber hinaus tragen sie zur Verifikation der Korrektheit des Programmes dar.
Die folgende Datei enthält das Ergebnis für das 3 x 3 - Brett.
Ausgabe_3x3.txt
Zur Erläuterung hier zwei Ausschnitte aus dieser Datei:
1.S.0.1
S S S
0 0 0
W W W
2.W.1.1 <----laufende Nummer der Stellung.Farbe, die gezogen hat.Baumtiefe.Position in der Warteliste
S S S
W 0 0
0 W W
3.S.2.1
S 0 S
W S 0
0 W W
4.W.3.1
S 0 S
W S W
0 W 0
S kann nicht mehr ziehen <---- unentschiedener Ausgang in diesem Zweig
5.W.3.2
S 0 S
W W 0
0 W 0
6.S.4.1
0 0 S
W S 0
0 W 0
7.W.5.1
W 0 S
0 S 0
0 W 0
W hat gewonnen <----- Gewinnstellung für Weiß
8.S.4.2
S 0 0
W W S
0 W 0
9.W.5.1
S W 0
W 0 S
0 W 0
W hat gewonnen
.
.
.
Der Aufbau des Stellungsgraphen beginnt natürlich bei der Grundstellung und schreitet von links nach rechts voran, d.h. die möglichen weißen Züge in dieser und allgemein jeder Stellung, in der Weiß am Zug ist, werden immer mit dem weißen Bauern geführt, der am weitesten links steht; gleiches gilt für die schwarzen Bauern. Zuerst wird versucht zu ziehen, dann nach links zu schlagen, dann nach rechts.
Bei jedem Halbzug wird die Stellungsanzeige ein Stück nach rechts gerückt; dies korrespondiert zu der Ziffer, die ich "Baumtiefe" genannt habe (Baumtiefe beginnt in der Grundstellung bei 0). Landet der Zweig aber an einem Endpunkt (Unentschieden oder Gewinn) wird auf der gleichen Baumtiefe mit dem nächsten möglichen Zug der gleichen Farbe fortgefahren. Hier nun wird die vierte Ausgabe, genannt "Position in der Warteliste" inkrementiert. Siehe dazu die Halbzüge mit den Nummern 3, 4 und 5. Ist die Warteliste leer, d.h. gibt es keinen weiteren Zug, reduziert sich die Baumtiefe bis zu der Posititon in der wieder ein Zug möglich ist (siehe Übergang von Halbzug 7 nach 8).
Der zweite Ausschnitt zeigt nun den Fall einer Doublette:
.
.
.
27.S.6.3
0 0 0
S S 0
0 0 0
W kann nicht mehr ziehen
28.S.4.3
S 0 0
S W S
0 0 W
29.W.5.1
S W 0
S 0 S
0 0 W
W hat gewonnen
30.W.5.2
W 0 0
S 0 S
0 0 W
W hat gewonnen
31.S.4.4
S 0 0
S S 0
0 0 W
32.W.5.1
S 0 0
S S W
0 0 0
33.S.6.1
S 0 0
0 S W
S 0 0
S hat gewonnen
34.S.6.2
S 0 0
S 0 W
0 S 0
S hat gewonnen
35.W.5.2
S 0 0
S W 0
0 0 0
36.S.6.1
S 0 0
0 W 0
S 0 0
S hat gewonnen
S0975812 000SS0000 Doublette Original: 27
37.W.3.2
S 0 S
W 0 0
0 0 W
.
.
.
Hier taucht zwischen dem 36. und 37. Halbzug eine schon einmal vorgekommenen Stellung auf, nämlich die mit der Nummer 27. Sie entsteht als zweite Position hinter dem Halbzug 35 und hätte eigentlich die Halbzugnummer 37. Im Falle von Dubletten wird aber der gesamte dahinter hängende Zweig ausgeblendet und auch in der Nummerierung der Halbzüge ignoriert. Man beachte, dass Doublette nicht nur Stellungsgleichheit bedeutet, sondern nur vorliegt, wenn auch die gleiche Farbe am Zug ist.
Am Ende der Datei folgen die eigentlich interessanten zusammenfassenden Ergebnisse der Analyse des Stellungsgraphen.
Anzahl Stellungen ohne Doubletten: 135
Anzahl Stellungen incl. Doubletten: 252
weisse Gewinne 58 schwarze Gewinne 50
unentschieden 26 maxtiefe: 7
maximale Laenge der Warteliste: 4
Anzahl der moeglichen Stellungen: 19683
Anzahl gefundener Doubletten: 117
Wie man sieht, gibt es fast so viele Doubletten wie Stellungen ohne Doubletten. Die Anzahl der Gewinnstellungen scheint eine höhere Gewinnchance für Weiß zu suggerieren; wie wir sehen werden ist diese Vermutung im Sinne einer optimalen Strategie aber grundfalsch.
Die Baumtiefe nimmt maximal den Wert 7 an und in der Warteliste stehen maximal 4 Elemente. Die Zählung der drei Ergebnistypen erfolgte inklusive der jeweiligen Doublettenzweige.
2. Aufgabe Gewinnstrategie, der Min - Max - Algorithmus
In der Mathematik gibt es ein Teilgebiet mit dem Namen Spieltheorie. Die Ergebnisse dieser Theorie machen Aussagen über den Ausgang und den Verlauf von Spielen. Der von John Forbes Nash entwickelte Min - Max - Algorithmus liefert Ergebnisse so genannter "2-Personen-Nullsummenspielen mit vollständiger Information". Bauernschach (wie auch Schach und andere Spiele) ist ein solches Spiel und der Min - Max lässt sich darauf anwenden. Die Grundidee ist die Bewertung jeder einzelnen Stellung nach den drei Kriterien "Weiß wird gewinnen", "Schwarz wird gewinnen" und "wird unentschieden ausgehen", wenn eine optimale Strategie angewendet wird; wir kürzen diese möglichen Ausgänge mit 1, -1 und 0 ab.
Dummerweise sieht man erst am Ende eines jeden Zweiges im Stellungsbaum, wie der Ausgang des Spieles an dieser Stelle ist, was bedeutet, dass nur bei genauer Kenntnis des Baumes eine genaue Vorhersage des Spielausganges möglich ist. Wie wird der Algorithmus nun angewendet? Nehmen wir an, der Spielbaum wäre komplett bestimmt. An jedem Ende eines Zweiges dieses Baumes bewertet man den Spielausgang mit 1, -1 oder 0 (da kennt man ja das Ergebnis) und verfolgt nun den Zweig zurück und bewertet alle Stellungen mit dem gleichen Wert bis zwei oder mehr Zweige zusammentreffen. Die dortige Stellung bekommt nun als Bewertung, und daher der Name des Algorithmus, das Maximum (oder das Minimum) der letzten Bewertungen bevor die Zweige aufeinandertreffen. Man nimmt das Maximum, wenn man eine Stellung bewertet, die einen Halbzug für Weiß beschreibt, entsprechend das Minimum, wenn ein Halbzug für Schwarz dran ist.
Folgender Ausschnitt aus der Visualisierung eines Spielbaumes zeigt die Anwendung des Algorithmus:

In der obigen Grafik sind die Bewertungen des Min - Max - Algorithmus an der linken unteren Ecke des Schachbrettes angezeigt. Die Bewertung der Startaufstellung zeigt letztlich das gewünschte Ergebnis: Bei optimaler Strategie kann Weiß als Startspieler höchstens ein Unentschieden erreichen. Aber auch die darunter liegenden Ebenen des Baumes zeigen relevante Zwischenergebnisse, z.B. zeigt die zweite Ebene, dass auch Schwarz unabhängig vom weissen Anfangszug ein Unentschieden erreichen kann, wenn es optimal spielt.
Die obige Grafik stellt das Ergebnis des 3 x 3 - Brettes ohne Doppelschritt dar.
Programmtechnisch wurde der Min - Max - Algorithmus bereits beim Aufbau des Stellungsgraphen angewendet und seine Ergebnisse in den Knoten des Graphen mit abgespeichert. Somit konnte die Ausgabe des Ergebnisses am Ende der jeweiligen Ausgabedatei bereits angezeigt werden:
Ergebnis des MinMax - Algorithmus: 0 <----- Wert für Weiß in der Grundstellung
0 0 0 <----- Werte für Schwarz im ersten Gegen(halb-)zug
Visualisierung
3. Aufgabe Visualisierung des Stellungsgraphen
Die Darstellung des Stellungsgraphen als Druckliste, wie oben in der Datei Aufgabe_3x3.txt gezeigt, erfüllt nicht die Ansprüche an eine übersichtliche Darstellung eines gerichteten Graphen; man möchte vielmehr die Knoten und die Kanten des Graphen auch als solche erkennen können.
Die Unterprogrammbibliothek des FPC (Free Pascal Compiler) bietet zu diesem Zweck eine Unit an, mit der man auf einer Bildschirmoberfläche zeichnen kann. Die habe ich benutzt, um den Stellungsgraphen darzustellen.
Folgendes Bild enthält den Graphen für das 3 x 3 Brett ohne Doppelschritt.

Ausgehend von der Grundstellung in der oberen linken Ecke werden die Knoten und Kanten des Graphen in den der Baumtiefe entsprechenden Ebenen angezeigt (Baumtiefe der Grundstellung = 0).
Die Farbgebung der Knoten hat folgende Bedeutung:
Grau - Zwischenstand
Rot - Endstand, Weiß gewinnt
Blau - Endstand, Schwarz gewinnt
Grün - Endstand, Unentschieden
Die Farbgebung der Kanten macht eine Aussage über die Doubletten; eine pinkfarbene Kante zeigt auf eine Doublette, d.h. eine mehrfach vorkommende Stellung.
Wie man sieht passt der Graph des einfachsten Spieles 3 x 3 ohne Doppelschritt gerade auf eine Bildschirmseite; schon bei Hinzunahme der Doppelschrittregel reicht der Graph über den Bildschrimrand hinaus. Daher kann man im ausführenden Programm die linke obere Ecke des Bildausschnittes festlegen, die Grundstellung hat die Position (1, 0). Das Programm malt dann den entsprechenden Ausschnitt, als ob man ein Fenster über den Gesamtgraphen geschoben hätte. Kanten ohne Anfangs- oder Endpunkt innerhalb des Fensters werden allerdings nicht dargestellt.
Siehe dazu folgendes Beispiel aus einem 4 x 4 - Stellungsgraphen.

Hier wurde die Position (6,9) gewählt, also ein Ausschnitt aus dem unteren Teil des Baumes.
Weitere Beispiele finden sich im Anhang.
Die Darstellung des Stellungsgraphen als Druckliste, wie oben in der Datei Aufgabe_3x3.txt gezeigt, erfüllt nicht die Ansprüche an eine übersichtliche Darstellung eines gerichteten Graphen; man möchte vielmehr die Knoten und die Kanten des Graphen auch als solche erkennen können.
Die Unterprogrammbibliothek des FPC (Free Pascal Compiler) bietet zu diesem Zweck eine Unit an, mit der man auf einer Bildschirmoberfläche zeichnen kann. Die habe ich benutzt, um den Stellungsgraphen darzustellen.
Folgendes Bild enthält den Graphen für das 3 x 3 Brett ohne Doppelschritt.

Ausgehend von der Grundstellung in der oberen linken Ecke werden die Knoten und Kanten des Graphen in den der Baumtiefe entsprechenden Ebenen angezeigt (Baumtiefe der Grundstellung = 0).
Die Farbgebung der Knoten hat folgende Bedeutung:
Grau - Zwischenstand
Rot - Endstand, Weiß gewinnt
Blau - Endstand, Schwarz gewinnt
Grün - Endstand, Unentschieden
Die Farbgebung der Kanten macht eine Aussage über die Doubletten; eine pinkfarbene Kante zeigt auf eine Doublette, d.h. eine mehrfach vorkommende Stellung.
Wie man sieht passt der Graph des einfachsten Spieles 3 x 3 ohne Doppelschritt gerade auf eine Bildschirmseite; schon bei Hinzunahme der Doppelschrittregel reicht der Graph über den Bildschrimrand hinaus. Daher kann man im ausführenden Programm die linke obere Ecke des Bildausschnittes festlegen, die Grundstellung hat die Position (1, 0). Das Programm malt dann den entsprechenden Ausschnitt, als ob man ein Fenster über den Gesamtgraphen geschoben hätte. Kanten ohne Anfangs- oder Endpunkt innerhalb des Fensters werden allerdings nicht dargestellt.
Siehe dazu folgendes Beispiel aus einem 4 x 4 - Stellungsgraphen.

Hier wurde die Position (6,9) gewählt, also ein Ausschnitt aus dem unteren Teil des Baumes.
Weitere Beispiele finden sich im Anhang.
Ergebnisse
Die bisherigen Ergebnisse für ein 3x3, 4x4 und 5x5 - Brett stelle ich zunächst als Kopie der Ausgabe am Ende der jeweiligen Stellungsbäume dar.
Ergebnisse für 3x3 (bereits oben angezeigt)
Anzahl Stellungen ohne Doubletten: 135
Anzahl Stellungen incl. Doubletten: 252
weisse Gewinne 58 schwarze Gewinne 50
unentschieden 26 maxtiefe: 7
maximale Laenge der Warteliste: 4
Anzahl der moeglichen Stellungen: 19683
Anzahl gefundener Doubletten: 117
Ergebnis des MinMax - Algorithmus: 0
0 0 0
Ergebnisse für 3x3 mit Doppelschritt
Anzahl Stellungen ohne Doubletten: 153
Anzahl Stellungen incl. Doubletten: 276
weisse Gewinne 72 schwarze Gewinne 60
unentschieden 26 maxtiefe: 7
maximale Laenge der Warteliste: 5
Anzahl der moeglichen Stellungen: 19683
Anzahl gefundener Doubletten: 123
Ergebnis des MinMax - Algorithmus: 1
0 1 0
Das Ergebnis des Min-Max-Algorithmus zeigt den wesentlichen Unterschied zwischen den Varianten mit und ohne Doppelschritt: Mit Doppelschritt hat Weiß eine ultimative Gewinnstrategie, was letztlich daran liegt, dass mit einem Doppelschritt die gegnerische Grundlinie erreicht werden kann.
Der folgende Ausschnitt des Stellungsgraphen zeigt die Situation der ersten 3 Halbzüge:
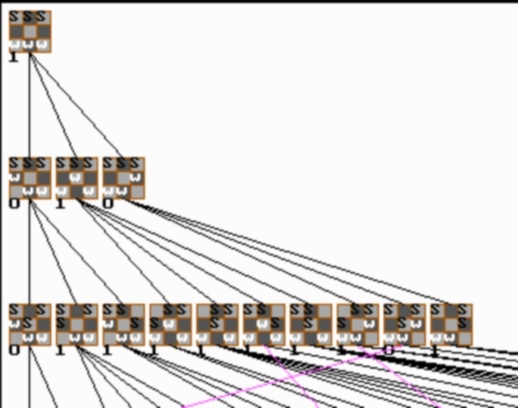
Wie man sieht führt nur der Anfangs-(halb-) Zug b1 - b2 zum Sieg von Weiß.
Im Anhang findet sich die Darstellung des kompletten Graphen für 3x3D.
Ergebnisse für 4x4:
Anzahl Stellungen ohne Doubletten: 20286
Anzahl Stellungen incl. Doubletten: 4197973
weisse Gewinne 1365654 schwarze Gewinne 907164
unentschieden 57538 maxtiefe: 17
maximale Laenge der Warteliste: 7
Anzahl der moeglichen Stellungen: 43046721
Anzahl gefundener Doubletten: 4177687
Ergebnis des MinMax - Algorithmus: 0
0 -1 -1 0
Die Anzahl der Doubletten schießt ab dieser Brettgröße enorm in die Höhe.
Hier ist das Beste erzwingbare Ergebnis für Weiß ein Unentschieden. Es gibt zwei initiale Verlustzüge von Weiß auf Brett 2 und 3 im 1. Halbzug.
Ergebnisse für 4x4 mit Doppelschritt:
Anzahl Stellungen ohne Doubletten: 33817
Anzahl Stellungen incl. Doubletten: 9404797
weisse Gewinne 2998208 schwarze Gewinne 2085122
unentschieden 137254 maxtiefe: 17
maximale Laenge der Warteliste: 9
Anzahl der moeglichen Stellungen: 43046721
Anzahl gefundener Doubletten: 9370980
Ergebnis des MinMax - Algorithmus: 0
-1 0 0 -1 0 0 0 0
Die Verdopplung der zweiten (Halb-) Zugebene von 4 auf 8 Stellungen ergibt sich aus der Möglichkeit schon im ersten Halbzug einen Doppelschritt zu machen (im Gegensatz zu der 3x3 - Konstellation).

Als weitere Farbgebung kommt das Gelb-Pinke Schachbrett hinzu, das einen Doppelschritt von der Grundlinie anzeigt.
Das vierte Brett hat als Min-Max_Wert die -1, was durch die Kanten des Graphen verdeckt wird.
Hier gibt es zwei initiale Verlustzüge von Weiß, nämlich die beiden Halbzüge in Brett 1 und 4 im 1. Halbzug.
Ergebnisse für 4x4 mit Schlagen im Vorbeigehen (i.V.):
Anzahl Stellungen ohne Doubletten: 40814
Anzahl Stellungen incl. Doubletten: 12078307
weisse Gewinne 3840694 schwarze Gewinne 2664120
unentschieden 201540 maxtiefe: 17
maximale Laenge der Warteliste: 9
Anzahl der moeglichen Stellungen: 43046721
Anzahl gefundener Doubletten: 12037493
Ergebnis des MinMax - Algorithmus: 0
0 -1 -1 0 -1 0 0 -1
Durch das Schlagen im Vorbeigehen erhöht sich die Anzahl der Verlustzüge für Weiß auf 4 von 8 Zügen im 1. Halbzug.
Ergebnisse für 5x5:
Anzahl Stellungen ohne Doubletten: 3210411
Anzahl Stellungen incl. Doubletten: 90627857597982
weisse Gewinne 29822877361856 schwarze Gewinne 25695319622490
unentschieden 70888237676 maxtiefe: 31
maximale Laenge der Warteliste: 9
Anzahl der moeglichen Stellungen: 847288609443
Anzahl gefundener Doubletten: 90627854387571
Ergebnis des MinMax - Algorithmus: 0
0 0 0 0 0
Hier wieder ein komplettes Unentschieden auf ganzer Linie.
Ergebnisse für 5x5 mit Doppelschritt:
Anzahl Stellungen ohne Doubletten: 5181470
Anzahl Stellungen incl. Doubletten: 359594600752789
weisse Gewinne 118880145796882 schwarze Gewinne 102433047937666
unentschieden 261918177270 maxtiefe: 31
maximale Laenge der Warteliste: 12
Anzahl der moeglichen Stellungen: 847288609443
Anzahl gefundener Doubletten: 359594595571319
Ergebnis des MinMax - Algorithmus: 0
0 0 0 0 0 0 0 0 0 0
Wie langweilig ...
Ergebnisse für 5x5 mit Schlagen im Vorbeigehen:
Anzahl Stellungen ohne Doubletten: 7148541
Anzahl Stellungen incl. Doubletten: 385353132712907
weisse Gewinne 127343684967876 schwarze Gewinne 109967444695092
unentschieden 295621421268 maxtiefe: 31
maximale Laenge der Warteliste: 12
Anzahl der moeglichen Stellungen: 847288609443
Anzahl gefundener Doubletten: 385353125564366
Ergebnis des MinMax - Algorithmus: 0
0 -1 -1 -1 0 0 0 0 0 0
Na immerhin, das i.V. bringt etwas Auflockerung in die Gewinnstrategie.
Ja und nun: 6x6?
Ich muß zugeben, dazu habe ich kein Ergebnis, warum sehen wir an folgender Tabelle, die die explodierende Anzahl der Züge darstellt.
Das Wachstum der Anzahl der Stellungen ohne und mit Doubletten ist exponentiell. Dies zeigen folgende Diagramme, bei denen der Logarithmus der Anzahl der Doubletten gegen die Anzahl der Felder des Schachbrettes aufgetragen ist. Die grüne Gerade ist eine lineare Regressionsgrade aus den jeweils 3 Datenpunkten (Anzahl Felder, ln(Anzahl Stellungen)).

Soweit der erste Teil der Ergebnisse zum Bauernschach. Der zweite Teil beschäftigt sich mit einem konkreten Programm zum Spielen von Bauernschach gegen den Computer, das ich in der nächsten Version meiner Webseite vorstellen werde.
Ergebnisse für 3x3 (bereits oben angezeigt)
Anzahl Stellungen ohne Doubletten: 135
Anzahl Stellungen incl. Doubletten: 252
weisse Gewinne 58 schwarze Gewinne 50
unentschieden 26 maxtiefe: 7
maximale Laenge der Warteliste: 4
Anzahl der moeglichen Stellungen: 19683
Anzahl gefundener Doubletten: 117
Ergebnis des MinMax - Algorithmus: 0
0 0 0
Ergebnisse für 3x3 mit Doppelschritt
Anzahl Stellungen ohne Doubletten: 153
Anzahl Stellungen incl. Doubletten: 276
weisse Gewinne 72 schwarze Gewinne 60
unentschieden 26 maxtiefe: 7
maximale Laenge der Warteliste: 5
Anzahl der moeglichen Stellungen: 19683
Anzahl gefundener Doubletten: 123
Ergebnis des MinMax - Algorithmus: 1
0 1 0
Das Ergebnis des Min-Max-Algorithmus zeigt den wesentlichen Unterschied zwischen den Varianten mit und ohne Doppelschritt: Mit Doppelschritt hat Weiß eine ultimative Gewinnstrategie, was letztlich daran liegt, dass mit einem Doppelschritt die gegnerische Grundlinie erreicht werden kann.
Der folgende Ausschnitt des Stellungsgraphen zeigt die Situation der ersten 3 Halbzüge:

Wie man sieht führt nur der Anfangs-(halb-) Zug b1 - b2 zum Sieg von Weiß.
Im Anhang findet sich die Darstellung des kompletten Graphen für 3x3D.
Ergebnisse für 4x4:
Anzahl Stellungen ohne Doubletten: 20286
Anzahl Stellungen incl. Doubletten: 4197973
weisse Gewinne 1365654 schwarze Gewinne 907164
unentschieden 57538 maxtiefe: 17
maximale Laenge der Warteliste: 7
Anzahl der moeglichen Stellungen: 43046721
Anzahl gefundener Doubletten: 4177687
Ergebnis des MinMax - Algorithmus: 0
0 -1 -1 0
Die Anzahl der Doubletten schießt ab dieser Brettgröße enorm in die Höhe.
Hier ist das Beste erzwingbare Ergebnis für Weiß ein Unentschieden. Es gibt zwei initiale Verlustzüge von Weiß auf Brett 2 und 3 im 1. Halbzug.
Ergebnisse für 4x4 mit Doppelschritt:
Anzahl Stellungen ohne Doubletten: 33817
Anzahl Stellungen incl. Doubletten: 9404797
weisse Gewinne 2998208 schwarze Gewinne 2085122
unentschieden 137254 maxtiefe: 17
maximale Laenge der Warteliste: 9
Anzahl der moeglichen Stellungen: 43046721
Anzahl gefundener Doubletten: 9370980
Ergebnis des MinMax - Algorithmus: 0
-1 0 0 -1 0 0 0 0
Die Verdopplung der zweiten (Halb-) Zugebene von 4 auf 8 Stellungen ergibt sich aus der Möglichkeit schon im ersten Halbzug einen Doppelschritt zu machen (im Gegensatz zu der 3x3 - Konstellation).

Als weitere Farbgebung kommt das Gelb-Pinke Schachbrett hinzu, das einen Doppelschritt von der Grundlinie anzeigt.
Das vierte Brett hat als Min-Max_Wert die -1, was durch die Kanten des Graphen verdeckt wird.
Hier gibt es zwei initiale Verlustzüge von Weiß, nämlich die beiden Halbzüge in Brett 1 und 4 im 1. Halbzug.
Ergebnisse für 4x4 mit Schlagen im Vorbeigehen (i.V.):
Anzahl Stellungen ohne Doubletten: 40814
Anzahl Stellungen incl. Doubletten: 12078307
weisse Gewinne 3840694 schwarze Gewinne 2664120
unentschieden 201540 maxtiefe: 17
maximale Laenge der Warteliste: 9
Anzahl der moeglichen Stellungen: 43046721
Anzahl gefundener Doubletten: 12037493
Ergebnis des MinMax - Algorithmus: 0
0 -1 -1 0 -1 0 0 -1
Durch das Schlagen im Vorbeigehen erhöht sich die Anzahl der Verlustzüge für Weiß auf 4 von 8 Zügen im 1. Halbzug.
Ergebnisse für 5x5:
Anzahl Stellungen ohne Doubletten: 3210411
Anzahl Stellungen incl. Doubletten: 90627857597982
weisse Gewinne 29822877361856 schwarze Gewinne 25695319622490
unentschieden 70888237676 maxtiefe: 31
maximale Laenge der Warteliste: 9
Anzahl der moeglichen Stellungen: 847288609443
Anzahl gefundener Doubletten: 90627854387571
Ergebnis des MinMax - Algorithmus: 0
0 0 0 0 0
Hier wieder ein komplettes Unentschieden auf ganzer Linie.
Ergebnisse für 5x5 mit Doppelschritt:
Anzahl Stellungen ohne Doubletten: 5181470
Anzahl Stellungen incl. Doubletten: 359594600752789
weisse Gewinne 118880145796882 schwarze Gewinne 102433047937666
unentschieden 261918177270 maxtiefe: 31
maximale Laenge der Warteliste: 12
Anzahl der moeglichen Stellungen: 847288609443
Anzahl gefundener Doubletten: 359594595571319
Ergebnis des MinMax - Algorithmus: 0
0 0 0 0 0 0 0 0 0 0
Wie langweilig ...
Ergebnisse für 5x5 mit Schlagen im Vorbeigehen:
Anzahl Stellungen ohne Doubletten: 7148541
Anzahl Stellungen incl. Doubletten: 385353132712907
weisse Gewinne 127343684967876 schwarze Gewinne 109967444695092
unentschieden 295621421268 maxtiefe: 31
maximale Laenge der Warteliste: 12
Anzahl der moeglichen Stellungen: 847288609443
Anzahl gefundener Doubletten: 385353125564366
Ergebnis des MinMax - Algorithmus: 0
0 -1 -1 -1 0 0 0 0 0 0
Na immerhin, das i.V. bringt etwas Auflockerung in die Gewinnstrategie.
Ja und nun: 6x6?
Ich muß zugeben, dazu habe ich kein Ergebnis, warum sehen wir an folgender Tabelle, die die explodierende Anzahl der Züge darstellt.
| 3x3 | 3x3D | 4x4 | 4x4D | 4x4iV | 5x5 | 5x5D | 5x5iV | |
| ohne Doubl. |
135 | 153 | 20286 | 33817 | 40814 | 3210411 | 5181470 | 7148541 |
| incl. Doubl. |
252 | 276 | 4197973 | 9404797 | 12078307 | 90627857597982 | 359594600752789 | 385353132712907 |
| maxtiefe | 7 | 7 | 17 | 17 | 17 | 31 | 31 | 31 |
| Warteliste | 4 | 5 | 7 | 9 | 9 | 9 | 12 | 12 |
| Rechenzeit | <10ms | <10ms | 0,54s | 1,03s | 1,35s | 201,13s | 387,32s | 619,94s |
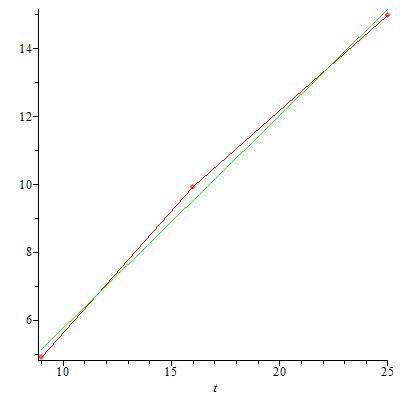
Das Wachstum der Anzahl der Stellungen ohne und mit Doubletten ist exponentiell. Dies zeigen folgende Diagramme, bei denen der Logarithmus der Anzahl der Doubletten gegen die Anzahl der Felder des Schachbrettes aufgetragen ist. Die grüne Gerade ist eine lineare Regressionsgrade aus den jeweils 3 Datenpunkten (Anzahl Felder, ln(Anzahl Stellungen)).


ohne Doubletten, ohne Doppelschritt ohne Doubletten, mit Doppelschritt
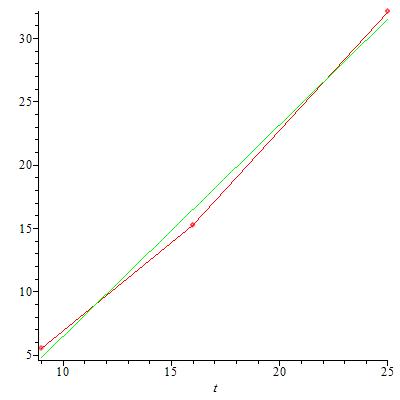
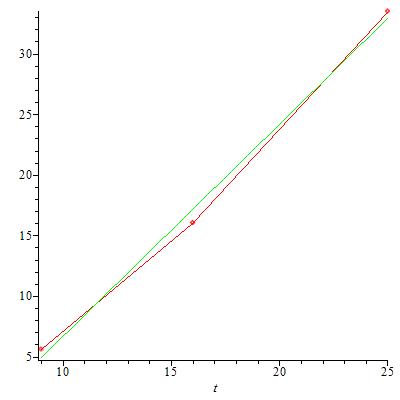
mit Doubletten, ohne Doppelschritt mit Doubletten, mit Doppelschritt
Dies bedeutet, dass der interne Ressourcenbedarf für das Berechnungsprogramm des Stellungsbaumes ebenfalls exponentiell anwächst. Konkret wächst beispielsweise die Größe der benötigten Hashtabelle zur Doublettenbestimmung im Fall der ersten Zeile um das weit über hundertfache gegenüber der 5x5 Version an. Da ein Eintrag in der Tabelle für 6x6 Bretter 26 Byte benötigen würde, wäre allein dafür ein Platz von ca. 100 Gb erforderlich, was den Hauptspeicherbedarf des Rechners doch erheblich übersteigt. Strategien zur Auslagerung auf Festplatte bringen dann natürlich erheblichen Mehrbedarf an Rechenzeit mit sich.

mit Doubletten, ohne Doppelschritt mit Doubletten, mit Doppelschritt
Verlängert man die grünen Geraden bis zum Abszissenwert 36, also der Feldanzahl eines 6x6 Feldes, erhält man Schätzwerte für die Anzahl der Stellungen für dieses Brett.
Folgende Werte ergeben sich:
Folgende Werte ergeben sich:
|
ohne Doubletten, ohne Doppelschritt
|
3,77 109 |
|
ohne Doubletten, mit Doppelschritt
|
8,19 109 |
|
mit Doubletten, ohne Doppelschritt
|
5,10 1021 |
|
mit Doubletten, mit Doppelschritt
|
5,08 1022 |
Soweit der erste Teil der Ergebnisse zum Bauernschach. Der zweite Teil beschäftigt sich mit einem konkreten Programm zum Spielen von Bauernschach gegen den Computer, das ich in der nächsten Version meiner Webseite vorstellen werde.
Anhang
Als erstes findet ihr hier die Dateien mit den Stellungsbäumen der untersuchten Spielvarianten:
3 x 3 ohne Doppelschritt (bereits oben eingestellt):
Ausgabe_3x3.txt
3 x 3 mit Doppelschritt:
Ausgabe 3x3D.txt
Alle weiteren Dateien sind komprimiert, die Originalgröße ist angegeben.
4 x 4 ohne Doppelschritt (5460 KB)
Ausgabe_4x4.zip
4 x 4 mit Doppelschritt (9233 KB)
Ausgabe_4x4D.zip
4 x 4 mit Doppelschritt und Schlagen i.V. (11640 KB)
Ausgabe_4x4iV.zip
Die folgenden 3 Ausgabedateien sind nach dem entkomprimieren so groß, dass die nicht von jedem Editor bearbeitet werden können. Mit dem allerdings kostenpflichtigen UltraEdit geht es sehr gut.
5 x 5 ohne Doppelschritt (1647986 KB)
Ausgabe_5x5.zip (Diese Datei kann bei Interesse per E-MAil angefordert werden)
5 x 5 mit Doppelschritt (2726585 KB)
Ausgabe_5x5D.zip (Diese Datei kann bei Interesse per E-MAil angefordert werden)
5 x 5 mit Doppelschritt und Schlagen i.V. (3958208 KB)
Ausgabe_5x5iV.zip (Diese Datei kann bei Interesse per E-MAil angefordert werden)
Einige Beispiele von gezeichneten Baumdiagrammen; es werden jeweils die Darstellungen ab Koordinate (x,y) ausgegeben:
Graph 3x3(1,0) (Bereits in Kapitel Visualisierung angezeigt)

Da der Zeichenbereich am rechten Rand etwas zu klein ist, wurden hier zwei Graphiken übereinander kopiert:
Graph 3x3Dkomplett(1,0)

Graph 4x4(1,0)

Graph 4x4D(1,0)
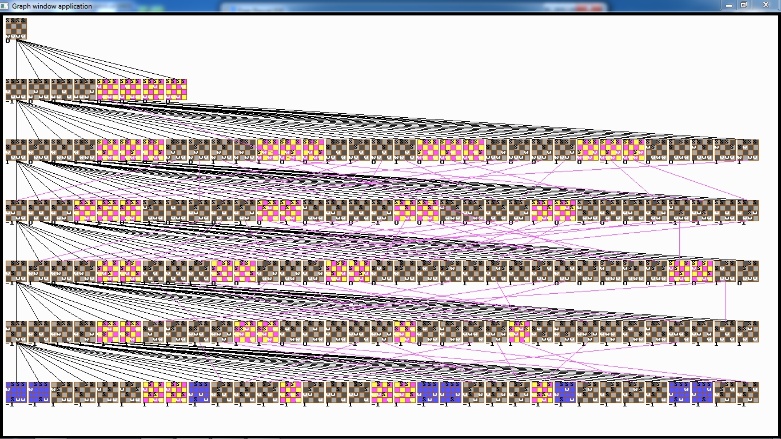
Graph 4x4iV(1,0)
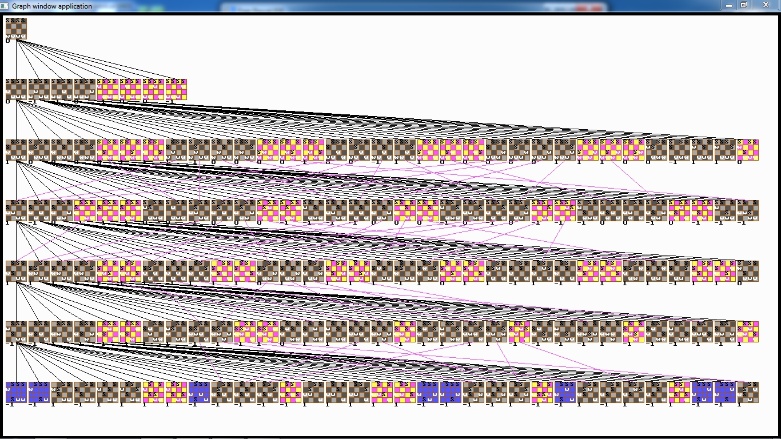
Graph 5x5(1,0)

Graph 5x5D(1,0)

Graph 5x5iV(1,0)

Das Programm zur Analyse des Bauernschach wird in einer der folgenden Versionen vorgestellt.
3 x 3 ohne Doppelschritt (bereits oben eingestellt):
Ausgabe_3x3.txt
3 x 3 mit Doppelschritt:
Ausgabe 3x3D.txt
Alle weiteren Dateien sind komprimiert, die Originalgröße ist angegeben.
4 x 4 ohne Doppelschritt (5460 KB)
Ausgabe_4x4.zip
4 x 4 mit Doppelschritt (9233 KB)
Ausgabe_4x4D.zip
4 x 4 mit Doppelschritt und Schlagen i.V. (11640 KB)
Ausgabe_4x4iV.zip
Die folgenden 3 Ausgabedateien sind nach dem entkomprimieren so groß, dass die nicht von jedem Editor bearbeitet werden können. Mit dem allerdings kostenpflichtigen UltraEdit geht es sehr gut.
5 x 5 ohne Doppelschritt (1647986 KB)
Ausgabe_5x5.zip (Diese Datei kann bei Interesse per E-MAil angefordert werden)
5 x 5 mit Doppelschritt (2726585 KB)
Ausgabe_5x5D.zip (Diese Datei kann bei Interesse per E-MAil angefordert werden)
5 x 5 mit Doppelschritt und Schlagen i.V. (3958208 KB)
Ausgabe_5x5iV.zip (Diese Datei kann bei Interesse per E-MAil angefordert werden)
Einige Beispiele von gezeichneten Baumdiagrammen; es werden jeweils die Darstellungen ab Koordinate (x,y) ausgegeben:
Graph 3x3(1,0) (Bereits in Kapitel Visualisierung angezeigt)

Da der Zeichenbereich am rechten Rand etwas zu klein ist, wurden hier zwei Graphiken übereinander kopiert:
Graph 3x3Dkomplett(1,0)

Graph 4x4(1,0)

Graph 4x4D(1,0)

Graph 4x4iV(1,0)

Graph 5x5(1,0)

Graph 5x5D(1,0)

Graph 5x5iV(1,0)

Das Programm zur Analyse des Bauernschach wird in einer der folgenden Versionen vorgestellt.