

Monte Carlo Methoden
 Flagge des Fürstentum Monaco
Flagge des Fürstentum Monaco"Mensch, Papa, warum fahren wir dahin nicht mal in Urlaub", meinte mein Sohn, nachdem er von einer Klassenfahrt nach Südfrankreich zurückgekommen war, "Monte Carlo ist super".
Da kann ich ihm nur zustimmen, auch ich war seinerzeit begeistert, auch ohne dass einer von uns beiden im Spielkasino gewesen wäre.
Jedenfalls erinnerte in mich in diesem Zusammenhang an eine Vorlesung während meines Studiums, die sich u.a. mit Monte Carlo Methoden beschäftigte; was also lag näher, als dieses Thema mal wieder aufzufrischen und etwas damit zu spielen, womit ein Zusammenhang zum Spielkasino hergestellt wäre. Gewinnen kann man hier wie dort vor allem Erkenntnisse; hier über einen originellen Zweig der numerischen Mathematik, dort, dass nur einer gewinnt, nämlich der monegassische Staat, der die Spielbanken betreibt.
Was hat also numerische Mathematik mit Monte Carlo zu tun?
Schon im Jahre 1727 entwickelte Georges-Louis Leclerc de Buffon, ein französischer Naturforscher, eine Methode zur Bestimmung der Kreiszahl π, die auf einem Zufallsexperiment beruht. Bei dem in der Folgezeit als Buffonsches Nadelproblem bekannt gewordenen Experiment wirft man eine Nadel auf ein Blatt Papier, das mit parallelen Linien versehen ist und notiert, wie oft die Nadel eine Linie trifft und wie oft nicht. Aus diesem Verhältnis kann man dann Pi näherungsweise berechnen.
Allgemein betrachtet wird eine Monte Carlo Methode dazu benutzt, mit Hilfe von Zufallszahlen mathematische Werte zu berechnen. Ich zeige in den folgenden Kapiteln unter Nutzung von FPC einige solcher Methoden und visualisiere ihre Ergebnisse.
Beginnen wir also gleich mit George-Louis.
Anhang
Über Zufallszahlen
Werkzeuge für die Programmerstellung
Da kann ich ihm nur zustimmen, auch ich war seinerzeit begeistert, auch ohne dass einer von uns beiden im Spielkasino gewesen wäre.
Jedenfalls erinnerte in mich in diesem Zusammenhang an eine Vorlesung während meines Studiums, die sich u.a. mit Monte Carlo Methoden beschäftigte; was also lag näher, als dieses Thema mal wieder aufzufrischen und etwas damit zu spielen, womit ein Zusammenhang zum Spielkasino hergestellt wäre. Gewinnen kann man hier wie dort vor allem Erkenntnisse; hier über einen originellen Zweig der numerischen Mathematik, dort, dass nur einer gewinnt, nämlich der monegassische Staat, der die Spielbanken betreibt.
Was hat also numerische Mathematik mit Monte Carlo zu tun?
Schon im Jahre 1727 entwickelte Georges-Louis Leclerc de Buffon, ein französischer Naturforscher, eine Methode zur Bestimmung der Kreiszahl π, die auf einem Zufallsexperiment beruht. Bei dem in der Folgezeit als Buffonsches Nadelproblem bekannt gewordenen Experiment wirft man eine Nadel auf ein Blatt Papier, das mit parallelen Linien versehen ist und notiert, wie oft die Nadel eine Linie trifft und wie oft nicht. Aus diesem Verhältnis kann man dann Pi näherungsweise berechnen.
Allgemein betrachtet wird eine Monte Carlo Methode dazu benutzt, mit Hilfe von Zufallszahlen mathematische Werte zu berechnen. Ich zeige in den folgenden Kapiteln unter Nutzung von FPC einige solcher Methoden und visualisiere ihre Ergebnisse.
Beginnen wir also gleich mit George-Louis.
Anhang
Über Zufallszahlen
Werkzeuge für die Programmerstellung
Das Buffonsche Nadelproblem

Buffon hat selber das Zufallsexperiment nicht mit einer Nadel und einem Blatt Papier, sondern mit Stöckchen auf einem gekachelten Fußboden durchgeführt. Aber mit Nadel und Papier ist es einfacher - man muss sich nicht so oft bücken - (wie es Mitte des 19. Jahrhunderts der Schweizer Astronom Rudolf Wolf machte), und heutzutage verwendet man natürlich ein Computerprogramm mit einem Zufallsgenerator.
Wie funktioniert das nun im Detail?
Der Abstand d der parallelen Linien muss größer sein, als die Länge l der Nadel. Es wird ein Schnittpunkt oder eine Berührung einer der Parallelen gezählt (Zähler P). Aus dem Verhältnis N/P der Gesamtzahl der Würfe N zu der Zahl der Berührungen P lässt sich die Zahl π berechnen:
Zur Herleitung dieser Formel benötigt man wahrscheinlichkeitstheoretische Überlegungen, die sehr anschaulich unter folgendem Link dargestellt sind: Herleitung Buffon.
Zur Simulation und Visualisierung habe ich ein Computerprogramm in Pascal (genauer FPC) geschrieben, das das Werfen der Nadel N-mal zufällig macht und die Treffer mit einer Parallele zählt. Um einen Eindruck von der Nadelverteilung zu bekommen, kann das Programm eine Computergrafik ausgeben, die die Lage aller geworfenen Nadeln zweifarbig darstellt; schneidende Nadeln werden grün, nicht schneidende rot dargestellt.
Für 5000 Würfe sieht das dann so aus:

Der hier berechnete Wert von 3,165 hat eine Abweichung von rund 0,73 % bezogen auf den richtigen Wert von 3,14159...
Der oben genannte Astronom Rudolf Wolf errechnete mit dieser Methode π zu 3,159; er allerdings hat die Nadeln einzeln geworfen.
Folgende Tabelle stellt die Ergebnisse für verschiedene Anzahl von Würfen zusammen:
Im Anhang steht das benutzte Programm für eigene Versuche zum Herunterladen bereit.
Anhang
MC_Pi_Buffon.pas
Wie funktioniert das nun im Detail?
Der Abstand d der parallelen Linien muss größer sein, als die Länge l der Nadel. Es wird ein Schnittpunkt oder eine Berührung einer der Parallelen gezählt (Zähler P). Aus dem Verhältnis N/P der Gesamtzahl der Würfe N zu der Zahl der Berührungen P lässt sich die Zahl π berechnen:
$\frac{N}{P} = \frac{\pi}{2} * \frac{d}{l}$
Zur Simulation und Visualisierung habe ich ein Computerprogramm in Pascal (genauer FPC) geschrieben, das das Werfen der Nadel N-mal zufällig macht und die Treffer mit einer Parallele zählt. Um einen Eindruck von der Nadelverteilung zu bekommen, kann das Programm eine Computergrafik ausgeben, die die Lage aller geworfenen Nadeln zweifarbig darstellt; schneidende Nadeln werden grün, nicht schneidende rot dargestellt.
Für 5000 Würfe sieht das dann so aus:

Der hier berechnete Wert von 3,165 hat eine Abweichung von rund 0,73 % bezogen auf den richtigen Wert von 3,14159...
Der oben genannte Astronom Rudolf Wolf errechnete mit dieser Methode π zu 3,159; er allerdings hat die Nadeln einzeln geworfen.
Folgende Tabelle stellt die Ergebnisse für verschiedene Anzahl von Würfen zusammen:
| Anzahl der Würfe |
berechn. Wert |
Anweichung in Prozent |
| 5000 |
3,165 |
0,73 |
| 100000 |
3,132 |
0,3 |
| 1000000 | 3,1390 | 0,08 |
| 10000000 | 3,14104 | 0,02 |
| 100000000 | 3,14164 | 0,002 |
Im Anhang steht das benutzte Programm für eigene Versuche zum Herunterladen bereit.
Anhang
MC_Pi_Buffon.pas
Es regnet Pi

Die Anzahl der Methoden um Pi zu berechnen ist riesig und auch unter den Monte Carlo Methoden gibt es mehrere Algorithmen, um zu einem Ergebnis zu kommen. Die folgende Methode lässt sich, wie wir sehen werden, auf andere Aufgabenstellungen verallgemeinern.
Denken wir uns einen kreisrunden Teich, der in einen quadratischen Teich bündig eingepasst ist und die voneinander nur durch eine (möglichst) dünne Wand getrennt sind. Beide Teiche sind zunächst leer und wir warten darauf, dass es anfängt zu regnen. Nicht nur so ein paar Tropfen, sondern ordentlich. Wenn der Regen aufgehört hat, messen wir die Wassermenge in beiden Teichen: des äußeren (Va) und des inneren (Vi). Die Gesamtmenge des Regenwassers entspricht der Fläche des Quadrates, die Menge des Wassers im kreisförmigen Teich der Fläche des Kreises, genauer: bildet man den Quotienten Vi / (Vi + Va) kürzt sich die in beiden Teichen gleichgroße Höhe h des Wasserstandes heraus:
Nun ist aber Fi ja gerade die Fläche des Kreises. Da Fi andererseits gleich π r2 ist und r = 0,5 (das Quadrat wird mit der Seitenlänge 1 angenommen), so berechnet sich π zu
Den Bau zweier solcher Teiche ersetzen wir nun durch ein zweidimensionales Modell und statt des Regens lassen wir Zufallstropfen aufs Blatt fallen. Außerdem reduzieren wir den Vollkreis auf einen Viertelkreis. Schreiben wir nun die Randbedingungen nochmals übersichtlich auf:
Quadrat der Seitenlänge 1 (in einem kartesischen Koordinatensystem [0, 1) x [0, 1)).
Darin einbeschrieben ein Viertelkreis mit Radius r = 1.
Ein Zufallstropfen ist ein Koordinatenpaar (x, y) zweier reeller Zufallszahlen jeweils zwischen 0 und 1.
Nun lässt man die Zufallstropfen regnen und zählt, wie viele im Kreis landen (innen) und wieviele außerhalb (außen). Genauso wie im obigen Beispiel kann man so π näherungsweise berechnen, nämlich:
Die Zählung innen versus außen erfolgt programmtechnisch über einen Vergleich am "Kreisrand" der Form x² + y² <= r²; erfüllt ein Zufallspunkt diesen Vergleich, liegt er innerhalb des Kreises (oder auf seinem Rand), sonst außerhalb.
Auch hierzu entstand ein kleines Programm, das ich mit einer Visualisierung des "Regnens" verbunden habe.
Das erste Bild, zeigt eine vergleichsweise geringe Anzahl von Regentropfen, nämlich 50000, sie sind hier zunächst in schwarzer Farbe dargestellt:

Da die Anzahl der Zufallspunkte in [0, 1) x [0, 1) (im nächsten Bild 1.000.000) allgemein um ein Vielfaches größer ist als die Anzahl der Bildschirmpixel, kommt es sehr schnell dazu, dass auf ein Bildschirmpixel mehrere Zufallsregentropfen fallen. Dies wird in der nächsten Darstellung durch eine immer dunklere Färbung der Pixel visualisiert:

Zum Vergleich dazu die Ausgabe von 100000 Regentropfen:

Auch bei diesem Beispiel hängt die Genauigkeit der Näherung an π von der Anzahl der Zufallspunkte ab. Folgende Tabelle zeigt einige Ergebnisse:
Der Vergleich zur Methode von Buffon wäre an dieser Stelle verfrüht, da einerseits keine Aussagen über den Zeitaufwand der Berechnungen gemacht wurden und andererseits hier nur punktuelle Ergebnisse, d.h. Ergebnisse einzelner Programmaufrufe aufgeschrieben wurden. Statt dessen sollte man Durchschnittswerte mehrerer Aufrufe bilden und dann vergleichen.
Im Anhang steht das benutzte Programm für eigene Versuche zum Herunterladen bereit.
MC_Pi_Regen.pas
Denken wir uns einen kreisrunden Teich, der in einen quadratischen Teich bündig eingepasst ist und die voneinander nur durch eine (möglichst) dünne Wand getrennt sind. Beide Teiche sind zunächst leer und wir warten darauf, dass es anfängt zu regnen. Nicht nur so ein paar Tropfen, sondern ordentlich. Wenn der Regen aufgehört hat, messen wir die Wassermenge in beiden Teichen: des äußeren (Va) und des inneren (Vi). Die Gesamtmenge des Regenwassers entspricht der Fläche des Quadrates, die Menge des Wassers im kreisförmigen Teich der Fläche des Kreises, genauer: bildet man den Quotienten Vi / (Vi + Va) kürzt sich die in beiden Teichen gleichgroße Höhe h des Wasserstandes heraus:
$\frac{V_i}{V_i + V_a} = \frac{hF_i}{hF_i + hF_a} = \frac{F_i}{F_i + F_a}$
$4 \frac{F_i}{F_i + F_a} = 4 \frac{V_i}{V_i + V_a}$
Quadrat der Seitenlänge 1 (in einem kartesischen Koordinatensystem [0, 1) x [0, 1)).
Darin einbeschrieben ein Viertelkreis mit Radius r = 1.
Ein Zufallstropfen ist ein Koordinatenpaar (x, y) zweier reeller Zufallszahlen jeweils zwischen 0 und 1.
Nun lässt man die Zufallstropfen regnen und zählt, wie viele im Kreis landen (innen) und wieviele außerhalb (außen). Genauso wie im obigen Beispiel kann man so π näherungsweise berechnen, nämlich:
$\pi = 4 \frac{innen}{innen + aussen}$
Auch hierzu entstand ein kleines Programm, das ich mit einer Visualisierung des "Regnens" verbunden habe.
Das erste Bild, zeigt eine vergleichsweise geringe Anzahl von Regentropfen, nämlich 50000, sie sind hier zunächst in schwarzer Farbe dargestellt:

Da die Anzahl der Zufallspunkte in [0, 1) x [0, 1) (im nächsten Bild 1.000.000) allgemein um ein Vielfaches größer ist als die Anzahl der Bildschirmpixel, kommt es sehr schnell dazu, dass auf ein Bildschirmpixel mehrere Zufallsregentropfen fallen. Dies wird in der nächsten Darstellung durch eine immer dunklere Färbung der Pixel visualisiert:

Zum Vergleich dazu die Ausgabe von 100000 Regentropfen:

Auch bei diesem Beispiel hängt die Genauigkeit der Näherung an π von der Anzahl der Zufallspunkte ab. Folgende Tabelle zeigt einige Ergebnisse:
| Anzahl der Zufallspunkte |
berechneter Wert von Pi |
Abweichung in % |
| 5000 |
3,169 |
0,87 |
| 10000 |
3.138 |
0,11 |
| 100000 | 3,136 | 0,19 |
| 1000000 | 3,1401 | 0,049 |
| 10000000 | 3,1414 | 0,007 |
| 100000000 | 3,14154 | 0,002 |
Der Vergleich zur Methode von Buffon wäre an dieser Stelle verfrüht, da einerseits keine Aussagen über den Zeitaufwand der Berechnungen gemacht wurden und andererseits hier nur punktuelle Ergebnisse, d.h. Ergebnisse einzelner Programmaufrufe aufgeschrieben wurden. Statt dessen sollte man Durchschnittswerte mehrerer Aufrufe bilden und dann vergleichen.
Im Anhang steht das benutzte Programm für eigene Versuche zum Herunterladen bereit.
MC_Pi_Regen.pas
Flächen unter Kurven

Das Vorgehen des letzten Abschnittes kann beliebig verallgemeinert werden: Jede auch krummlinig begrenzte Fläche über dem Intervall [a, b) kann auf diese Weise angenähert werden; es wird in der Literatur auch als "Hit or Miss" - Methode bezeichnet. Allerdings kennt die numerische Mathematik eine Fülle anderer Verfahren zur Flächenberechnung, die schnellere und genauere Ergebnisse liefern können. Es gibt jedoch Fälle, in denen Monte Carlo Methoden überlegen sind und Fälle, in denen es überhaupt keine andere Möglichkeit zur Berechnung gibt als diese. Beides möchte ich in den nächsten Abschnitten darstellen.
Betrachten wir dazu eine Funktion f(x) := -x2 + 1 auf dem Definitionsbereich [0, 1). Die Fläche unter der Kurve lässt sich mit einfachen Mitteln der Integralrechnung zu 2/3 leicht berechnen, sie soll ja hier auch nur als Beispiel dienen.
Grundsätzlich kann auch hier die "Regenmethode" angewendet werden, das folgende Bild zeigt ohne weitere Betrachtung eine Visualisierung für 1.000.000 Regentropfen, mit dem Ergebnis 0,6668.

Aber man kann die Zufälligkeit hier auch anders anwenden. Die folgende Formel erlaubt ebenfalls die Berechnung der Fläche unter der Kurve in Intervall [a, b):
Dabei sind die xi zufällig im Intervall [a, b) verteilt. Anschaulich wird hier die Fläche unter der Funktion f(x) mit Rechtecken der Breite (b - a) / N und der Höhe f(xi) angenähert.
Der Monte Carlo - Ansatz besteht hier im Zufall der Auswahl der Stützpunkte xi.
Es besteht sehr wohl ein Zusammenhang zwischen dieser Berechnungsmethode und der "Hit or Miss" (also der Regenmethode), der im Anhang erläutert wird.
In obigem Beispiel ist a = 0, b = 1.
Die Visualisierung erfolgt so, dass die Rechtecke um den jeweiligen Stützpunkt dargestellt werden, im folgenden für 10 und für 100 Stützpunkte.
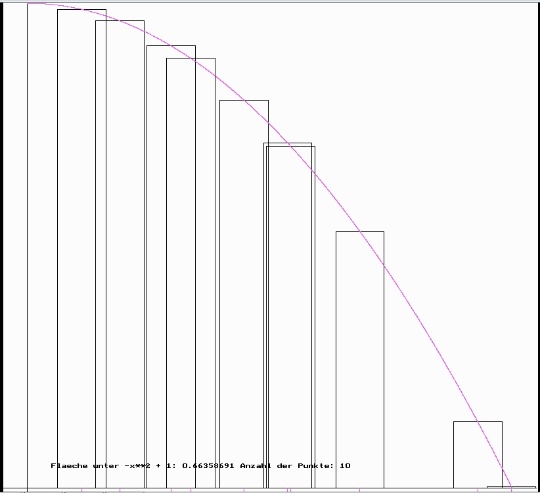
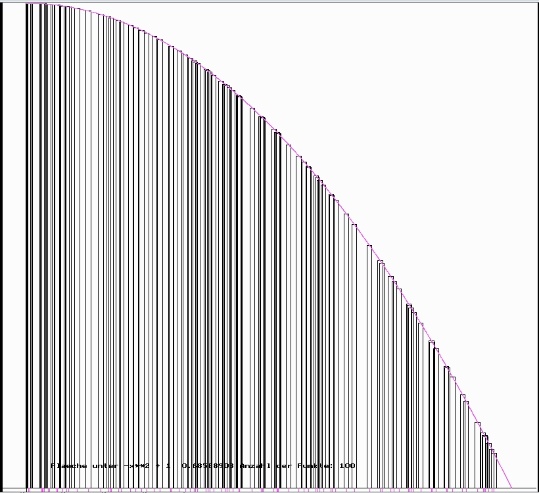
Folgende Tabelle zeigt die Ergebnisse für verschiedene N:
Auch hier wurden keine Mittelwerte über mehrere Berechnungen gebildet.
Wie schon oben erwähnt ist im Zweidimensionalen (also bei der Berechnung von Flächen), die Monte Carlo Methode den klassischen Verfahren unterlegen. Jedoch kann man sie auch in höheren Dimensionen zur Volumenberechnung verwenden (natürlich sprechen wir im 3 - dimensionalen und in höheren Dimensionen allgemein vom "Volumen" und nicht mehr von Fläche). Weitergehende Untersuchungen zeigen, dass Monte Carlo Methoden zur Volumenberechnung ab der 6. Dimension erheblich weniger Rechenaufwand benötigen, als klassische Verfahren (siehe dazu dieses Dokument).
Im Anhang steht das benutzte Programm für eigene Versuche zum Herunterladen bereit.
MC_Int_Regen.pas
MC_Int_xab.pas
MC_Int_xab_graph.pas
Das folgende Dokument stellt mathematische Grundlagen der benutzten Monte Carlo Integrationsmethoden zusammen.
Monte Carlo Mathematik
Betrachten wir dazu eine Funktion f(x) := -x2 + 1 auf dem Definitionsbereich [0, 1). Die Fläche unter der Kurve lässt sich mit einfachen Mitteln der Integralrechnung zu 2/3 leicht berechnen, sie soll ja hier auch nur als Beispiel dienen.
Grundsätzlich kann auch hier die "Regenmethode" angewendet werden, das folgende Bild zeigt ohne weitere Betrachtung eine Visualisierung für 1.000.000 Regentropfen, mit dem Ergebnis 0,6668.

Aber man kann die Zufälligkeit hier auch anders anwenden. Die folgende Formel erlaubt ebenfalls die Berechnung der Fläche unter der Kurve in Intervall [a, b):
$\text{Flaeche unter der Kurve :=}\frac{b - a}{N}(f(x_1) + f(x_2) + f(x_3) + ... +f(x_N)) =$
$\sum_{i=1}^N f(x_i) $
Der Monte Carlo - Ansatz besteht hier im Zufall der Auswahl der Stützpunkte xi.
Es besteht sehr wohl ein Zusammenhang zwischen dieser Berechnungsmethode und der "Hit or Miss" (also der Regenmethode), der im Anhang erläutert wird.
In obigem Beispiel ist a = 0, b = 1.
Die Visualisierung erfolgt so, dass die Rechtecke um den jeweiligen Stützpunkt dargestellt werden, im folgenden für 10 und für 100 Stützpunkte.


Folgende Tabelle zeigt die Ergebnisse für verschiedene N:
| Anzahl der Zufallspunkte |
berechneter Wert der Fläche |
Abweichung in % |
| 1000 |
0,674 |
1,2 |
| 10000 |
0,670 |
0,57 |
| 100000 | 0,668 | 0,25 |
| 1000000 | 0,667 | 0,07 |
| 10000000 | 0,6665 | 0,021 |
| 100000000 | 0,6667 | 0,0079 |
Auch hier wurden keine Mittelwerte über mehrere Berechnungen gebildet.
Wie schon oben erwähnt ist im Zweidimensionalen (also bei der Berechnung von Flächen), die Monte Carlo Methode den klassischen Verfahren unterlegen. Jedoch kann man sie auch in höheren Dimensionen zur Volumenberechnung verwenden (natürlich sprechen wir im 3 - dimensionalen und in höheren Dimensionen allgemein vom "Volumen" und nicht mehr von Fläche). Weitergehende Untersuchungen zeigen, dass Monte Carlo Methoden zur Volumenberechnung ab der 6. Dimension erheblich weniger Rechenaufwand benötigen, als klassische Verfahren (siehe dazu dieses Dokument).
Im Anhang steht das benutzte Programm für eigene Versuche zum Herunterladen bereit.
MC_Int_Regen.pas
MC_Int_xab.pas
MC_Int_xab_graph.pas
Das folgende Dokument stellt mathematische Grundlagen der benutzten Monte Carlo Integrationsmethoden zusammen.
Monte Carlo Mathematik
Wie dick ist das Apfelmännchen?
 Die Mandelbrotmenge, auch Apfelmännchen genannt
Die Mandelbrotmenge, auch Apfelmännchen genanntIn den letzten Jahren gewinnt die sog. Chaostheorie als scheinbare Widerlegung der Mathematik und der Physik immer mehr Bedeutung in der populärwissenschaftlichen Darstellung beider Wissenschaften. Dabei ist die Chaostheorie ein etablierter Zweig der Mathematik und steht keineswegs im Widerspruch zu ihr. Die hohe Popularität dieses mathematischen Teilgebietes erklärt sich u.a. aus der künstlerisch anmutenden Darstellung der Fraktale, die durch Methoden der Computer Science erst möglich wurden.
Zu den berühmtesten Fraktalen gehört die Mandelbrotmenge, die wegen ihres Aussehens auch "Apfelmännchen" genannt wird.
Die Definition dieser Menge ist vergleichsweise schlicht und verrät nichts über ihr wunderbares Aussehen. Typischerweise wird diese Menge als Teilmenge der komplexen Zahlen betrachtet, aber es geht genauso gut in einem reellen (x,y) - Koordinatensystem. Also:
Ein Punkt c der komplexen Zahlenebene gehört zur Mandelbrotmenge M, wenn die iterativ definierte Folge zn+1 = zn2 + c, z0 = 0, konvergiert, also einem festen Wert entgegenstrebt.
(Ohne Kenntnis von komplexen Zahlen liest sich die Definition wie folgt:
ein Punkt (cx, cy) gehört zur Mandelbrotmenge M, wenn die iterativ definierte Folge im IR2
(xn+1, yn+1) = (xn2 - yn2 , 2*xnyn) + (cx, cy), (x0, y0) = (0, 0) konvergiert.)
Für unser Thema ist die Menge M deshalb so interessant, weil keine Funktion bekannt ist, die die Begrenzungslinie der Menge beschreiben würde, obwohl die Menge immerhin zusammenhängend ist. Deshalb ist dies ein typisches Beispiel für die Flächenberechnung einer Menge, die sinnvollerweise mit einer Monte Carlo Methode erfolgt. Das folgende Bild zeigt M (schwarzer Anteil, obere Hälfte); es wurde parallel zu einer Flächenberechnung von M gezeichnet, wobei die Anzahl der "Regenpunkte" N = 40.000.000 betrug. Der Näherungswert für die Fläche betrug 1,50655. Der genaue Wert ist nicht bekannt. Siehe hierzu auch beispielsweise den Eintrag bei Wikipedia.

Die x-Achse ist die untere Begrenzung der halben Mandelbrotmenge in der Zeichnung, sie ist gleichzeitig Symmetrieachse. Die senkrechte y-Achse ist ebenfalls im oberen Bereich sichtbar. Die Begrenzung der Grafik lag bei [-2, 1) x [0, 1,2). Die Berechnung auf meinem PC dauerte ca. 2 1/2 Stunden.
Im Anhang steht das benutzte Programm für eigene Versuche zum Herunterladen bereit.
MC_Mandel.pas
Zu den berühmtesten Fraktalen gehört die Mandelbrotmenge, die wegen ihres Aussehens auch "Apfelmännchen" genannt wird.
Die Definition dieser Menge ist vergleichsweise schlicht und verrät nichts über ihr wunderbares Aussehen. Typischerweise wird diese Menge als Teilmenge der komplexen Zahlen betrachtet, aber es geht genauso gut in einem reellen (x,y) - Koordinatensystem. Also:
Ein Punkt c der komplexen Zahlenebene gehört zur Mandelbrotmenge M, wenn die iterativ definierte Folge zn+1 = zn2 + c, z0 = 0, konvergiert, also einem festen Wert entgegenstrebt.
(Ohne Kenntnis von komplexen Zahlen liest sich die Definition wie folgt:
ein Punkt (cx, cy) gehört zur Mandelbrotmenge M, wenn die iterativ definierte Folge im IR2
(xn+1, yn+1) = (xn2 - yn2 , 2*xnyn) + (cx, cy), (x0, y0) = (0, 0) konvergiert.)
Für unser Thema ist die Menge M deshalb so interessant, weil keine Funktion bekannt ist, die die Begrenzungslinie der Menge beschreiben würde, obwohl die Menge immerhin zusammenhängend ist. Deshalb ist dies ein typisches Beispiel für die Flächenberechnung einer Menge, die sinnvollerweise mit einer Monte Carlo Methode erfolgt. Das folgende Bild zeigt M (schwarzer Anteil, obere Hälfte); es wurde parallel zu einer Flächenberechnung von M gezeichnet, wobei die Anzahl der "Regenpunkte" N = 40.000.000 betrug. Der Näherungswert für die Fläche betrug 1,50655. Der genaue Wert ist nicht bekannt. Siehe hierzu auch beispielsweise den Eintrag bei Wikipedia.

Die x-Achse ist die untere Begrenzung der halben Mandelbrotmenge in der Zeichnung, sie ist gleichzeitig Symmetrieachse. Die senkrechte y-Achse ist ebenfalls im oberen Bereich sichtbar. Die Begrenzung der Grafik lag bei [-2, 1) x [0, 1,2). Die Berechnung auf meinem PC dauerte ca. 2 1/2 Stunden.
Im Anhang steht das benutzte Programm für eigene Versuche zum Herunterladen bereit.
MC_Mandel.pas
Logarithmus Naturalis von 2
Im Kapitel "Die Gefangenen von Zyklonien" unter "Aufgaben und Lösungen" auf dieser Web - Seite ist indirekt eine Monte Carlo Methode beschrieben mit der man ln(2) näherungsweise berechnen kann. Die Methode beruht auf der zufälligen Erzeugung von Zyklen der Länge k einer Permutation der Länge n (n gerade), wobei k > n/2 ist. Dort wurde im Anhang (Zyklen.pdf) gezeigt, dass die Wahrscheinlichkeit einen solchen Zyklus der Länge k > n/2 zu erhalten gleich
ist. Diese Summe konvergiert für wachsendes n gegen ln(2).
Die Monte Carlo Methode besteht also jetzt darin, mittels eines Programmes für großes n die Häufigkeit solcher Zyklen zu simulieren.
Für n = 10000 wurde ein Wert von 0,6921 bei einer prozentualen Abweichung von 0,1 % berechnet.
$\frac{1}{\frac{n}{2} + 1} + \frac{1}{\frac{n}{2} + 2} + \frac{1}{\frac{n}{2} +3}+ ... + \frac{1}{n} = \sum_{i=1}^{\frac{n}{2}} \frac{1}{\frac{n}{2}+i}$
Die Monte Carlo Methode besteht also jetzt darin, mittels eines Programmes für großes n die Häufigkeit solcher Zyklen zu simulieren.
Für n = 10000 wurde ein Wert von 0,6921 bei einer prozentualen Abweichung von 0,1 % berechnet.