Von 2 zu 3D
Stereographie
Nun gibt ja dreidimensionale Darstellungen auf zweidimensionalem Träger, z.B. die Stereofotografie oder Hologramme und man könnte auf die Idee kommen aus einer zweidimensionalen Darstellung eines dreidimensionalen Objektes ein dreidimensionales Bild zu erzeugen, das eben als solches wahrgenommen werden kann - und so kam ich auf diese Idee.
Bei der Überlegung, wie das zu bewerkstelligen wäre, war schnell klar, was alles nicht geht: Hologramm - viel zu aufwändig und teuer, Fotografieren in 3D mit entsprechender Kamera - gilt das gleiche, außerdem braucht man in beiden Verfahren ein tatsächliches dreidimensionales Modell. Das ist aber gar nicht der Ausgangspunkt, sondern Vorlage sollte ja eine zweidimensionale Darstellung sein.
Also braucht man etwas Physik, etwas Medizin, etwas Mathematik, etwas Informatik, ein gutes Programmiertool und - eine 3D-Brille, um ein Stereogramm mit eigenen Augen dreidimensional sehen zu können. Als geeignetes, weil preiswertes und relativ einfach umzusetzendes Verfahren bot sich also die Erzeugung eines sogenannten Anaglyphenbildes mit Hilfe eines grafikfähigen Programmes an, das mit einer Zweifarbenbrille, z.B. einer Rot/Türkis (=Cyan) - Brille dreidimensional betrachtet werden kann.
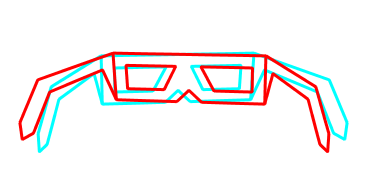
Die obige Abbildung 1 einer Rot/Türkis - Brille auf der linken Seite ist übrigens ein gutes Beispiel dafür, welcher Informationsverlust auf dem Weg von einer dreidimensionalen Darstellung zu einer zweidimensionalen Darstellung erfolgen kann. Je nachdem, wie man das Bild betrachtet, kann es die Darstellung einer Brille sein, die man so hält, dass man sie aufsetzen kann oder gerade umgekehrt, also mit Ohrbügeln, die vom Betrachter weg zeigen; in einem dreidimensionalen Bild, erkennt man die korrekte Lage des Gegenstandes, die zweidimensionale lässt beide Möglichkeiten offen. Was ist hier tatsächlich richtig? Gemeint ist hier die Lage der Brille, die zum Aufsetzen gebraucht wird, also mit dem roten Glas vor dem linken Auge. Und wenn man sich die jetzt aufsetzen würde, dann sähe man die Abbildung 2 dreidimensional.
Ich habe in meinem bisherigen Text viel zu viele Voraussetzungen gemacht, die ich weder erwähnt noch erläutert habe. Deshalb will ich als erstes ein paar erklärende Sätze über dreidimensionales Sehen und seine zweidimensionale Simulation schreiben, um das Thema verständlicher zu machen und dann auf meine Lösung eingehen. (Wie auch in meinen anderen Aufsätzen füge ich fachlich detailliertere Kapitel als Anhänge dazu.) Aber schon mal vorab: um die Anaglyphenbilder in diesem Aufsatz dreidimensional ansehen zu können braucht man eine Rot/Cyan - Brille einfachster Bauart, wie es sie für wenige Euro als Pappgestell zu kaufen gibt. Die RGB-Farbcodes von rot sind FF 00 00 (255, 0, 0) und die von Cyan 00 FF FF (0, 255, 255). Der Betrachtungsabstand sollte um die 30 cm liegen, hängt aber von der Größe der Darstellung auf dem jeweiligen Bildschirm ab. Je größer die Abbildung ist, desdo weiter weg sollte man sie betrachten. Beim Ansehen einer Anaglyphe mit einer solchen Brille, braucht das Gehirn eine gewisse "Umschaltzeit", bis es tatsächlich einen dreidimensionalen Eindruck hat. Diese Dauer liegt bei mir im Bereich von 5 -10 Sekunden, bei anderen Menschen mag sie anders sein. Allerdings gibt es auch Menschen, die überhaupt nicht dreidimensional sehen können - und damit sind nicht nur Einäugige gemeint- aber ich greife schon wieder vor.
Warum sehen wir dreidimensional?
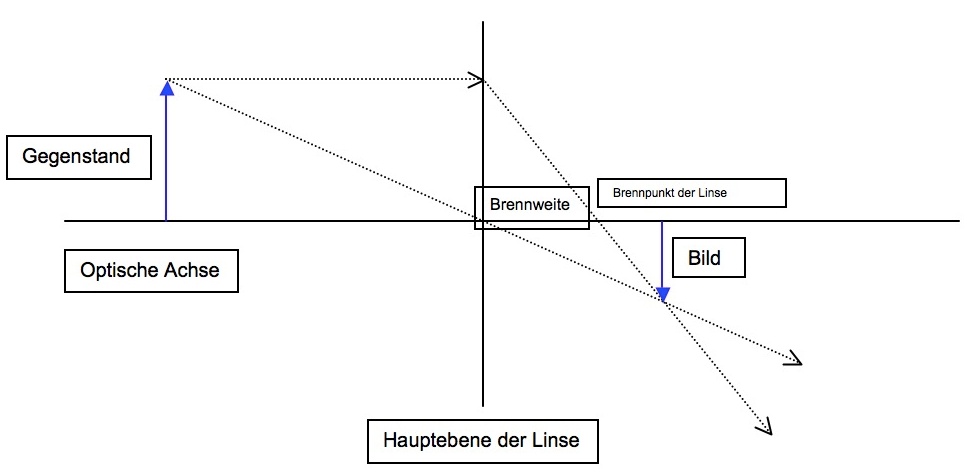
Erläuterung zur Abbildung: Die optische Achse geht durch die Mitte einer dünnen Linse, hier durch ihre Hauptebene dargestellt. Die Brennweite der Linse ist der Abstand der Hauptebene vom Brennpunkt der Linse; in ihm sammelt die Linse parallel einfallende Lichtstrahlen (wie sie wegen ihrer großen Entfernung z.B. von der Sonne bei uns ankommen, Brennglaseffekt). Um einen Gegenstand abzubilden, zieht man von einem seiner Punkte (sinnvollerweise die Spitze) zwei (fiktive) Strahlen, den Mittelpunktsstrahl durch den Kreuzungspunkt von Hauptebene und optischer Achse und den Achsenparallel-/Brennstrahl, der durch den Brennpunkt der Linse geht. Da wo sich die beiden Strahlen scheiden, liegt der Bildpunkt. Die obige Abbildung 3 zeigt eine Darstellung in einer Ebene, aber natürlich gilt diese Konstruktion auch, wenn man eine dreidimensionale Betrachtungsweise heranzieht, also die optische Achse als Drehachse verwendet. Da wir uns ja hier mit dreidimensionalen Darstellungen beschäftigen, was liegt näher, als dies auch mal eben einzugeben und anzuschauen:

Konstruktion der Abbildung mit dem Programm (die kreisförmige Linse wird als 36-Eck angenähert)

Betrachtung dieser Konstruktion von der Seite mit ausgeblendeten Konstruktionspunkten
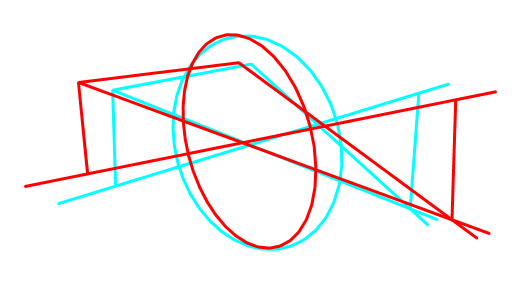
Dreidimensionales Anaglyphenbild unter gleichem Blickwinkel wie in Abb. 4
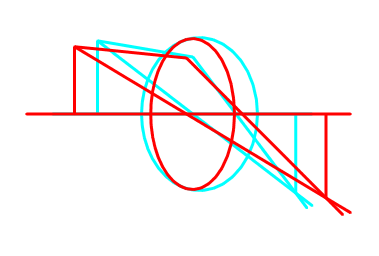
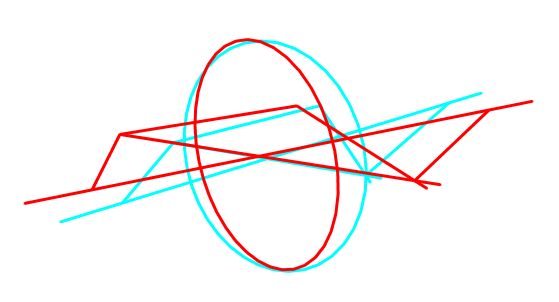
Dreidimensionales Anaglyphenbild mit schräg stehendem Gegenstand (und Bild)
Weiterhin gelten einige Einschränkungen bzw. Vereinfachungen für die Konstruktion: Eigentlich hat jede Linse zwei Hauptebenen, aber bei "dünnen" Linsen liegen sie so nahe beieinander, dass man sie wie eine Ebene ansehen kann. Die geometrische Abbildungsmethode ist nur für Punkte "in der Nähe" der optischen Achse ungefähr richtig. Die Konstruktion des Bildpunktes erfolgt immer in seiner Schärfeebene, d.h. zwei Objekte mit unterschiedlichen Abständen zur Hauptebene erzeugen auch in unterschiedlichen Abständen zur Hauptebene scharfe Bilder.
Die fast kreisförmige Zeichnung der Linse erfolgte mit 36 Eckpunkten (Abbildung 4). In Abbildung 5 wurde alles überflüssige weggelassen und die Figur von der Seite betrachtet und ergibt somit genau die Abbildung 3. Bei Abbildung 8 wurde der Gegenstand und damit auch sein Bild um 45° mit dem Uhrzeigersinn gedreht, um zu demonstrieren, dass die Abbildung nicht auf eine Ebene beschränkt ist.
Anhang: Die Linsenformel
Das zweite Auge nun sieht fast das gleiche Bild, aber eben nur fast, denn es befindet sich im ungefähren Abstand von 6,5 cm (Durchschnittswert beim Menschen) neben dem ersten. Und dieser kleine Unterschied, auf den es im Leben ja bekanntlich oft ankommt, ermöglicht dem Gehirn bei der Übereinanderlegung der beiden Bilder ein räumliches Sehen. Wie groß dieser Unterschied der beiden Bilder ist, hängt von der Entfernung des betrachteten Gegenstandes vom Gesicht des Menschen ab; je weiter weg er ist, desdo geringer ist der Unterschied und desdo geringer ist auch der räumliche Eindruck, den der Gegenstand macht. Wie schon gesagt, auch die Schärfe oder genauer gesagt die Fokussierung spielt bei der Beurteilung, wie weit ein Gegenstand entfernt ist, eine wichtige Rolle; das Gehirn weiß auf welchen Gegenstand es sein Auge scharf eingestellt (fokussiert) hat und schließt daraus ebenfalls auf die Entfernung oder besser: es weiß, ob Gegenstand A weiter oder weniger weit entfernt ist, als Gegenstand B. Wir wollen aber den Aspekt der Schärfe im Folgenden außer Acht lassen und betrachten alle Gegenstände, die wir hier beäugen, als scharf, was im Rahmen der Schärfentiefe (oder Tiefenschärfe) des Auges auch vertretbar ist.
Erste Beispiele:
Als erstes verweise ich auf ein Bild, das ich im Internet bei Wikipedia gefunden habe. Es stellt eine fiktive Landschaft dar mit einer Bergsilhouette im Hintergrund, einem Baum in der Mitte und einer schnurgeraden Straße, die aus dem Vordergrund bis in den Hintergrund zu den Bergen führt. Durch eine 3-D Brille betrachtet, erscheint ein deutlich dreidimensionales Bild mit einem starken räumlichen Eindruck.
Ich habe mal versucht, dieses Bild mit meinem Programm ungefähr nachzustellen und die Abbildung hier eingefügt.
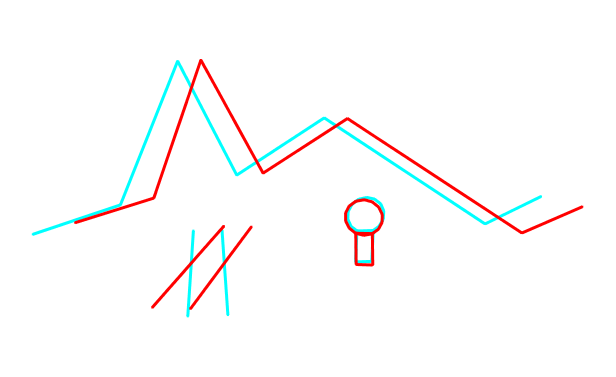
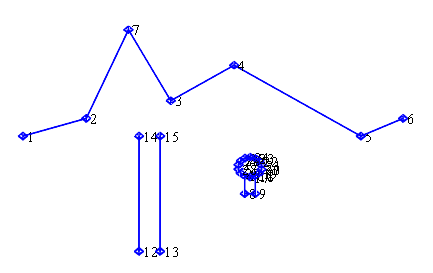
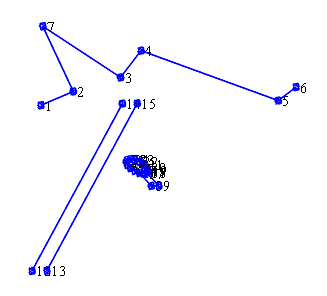
Bildkonstruktion der darüber stehenden Abbildung von vorne und rechts oben
Wo liegen die Unterschiede? Meine Vorlage, auf deren Erstellung ich noch ausführlich eingehen werde, ist ein Kantenmodell, das in seiner Entstehung tatsächlich dreidimensionale Koordinaten verwendet und das dann durch das entwickelte Programm als Anaglyphenbild umgerechnet wird (siehe Abbildung 9, 10 und 11). Die Darstellung aus Wikipedia geht von 2 zweidimensionalen Bildern aus, die ebenfalls zu einem Anaglyphenbild zusammengesetzt wurden.
Am deutlichsten sieht man den Unterschied in der Straße. Hier wurde in dem Wikipedia-Modell das Zusammenlaufen der beiden Straßenseiten künstlich hergestellt, um den „räumlichen Eindruck zu verstärken. Bei meinem Bild laufen die beiden Seiten in der Entfernung auch zusammen, aber aufgrund der vorliegenden Proportionen nur geringfügig.
Ein zweites Beispiel ist das bereits oben abgebildete Brillengestell (Abbildung 2). Auch hier zeige ich noch einige Abbildungen aus unterschiedlichen Perspektiven mit den zugehörigen Urbildern.
Simulation eines dreidimensionalen Bildes (Anaglyphenbild):
Um nun ein Anaglyphenbild zu erzeugen, das bei Betrachtung mit geeigneter Brille ein dreidimensionales Bild zeigt, muss man das Gehirn praktisch überlisten, indem man jedem Auge ein anderes zweidimensionales Bild zeigt, die dann vom Gehirn zu einem dreidimensionalen zusammengesetzt wird. Die unterschiedlichen Farben (z.B. Rot / Cyan) des Bildes bzw. der Brille sorgen dafür, dass jedes Auge nur den Anteil des betrachteten Anaglyphenbildes wahrnimmt, der auch bei einem realen dreidimensionalen Gegenstand von dem jeweiligen Auge gesehen würde.
Es gibt anspruchsvollere Anaglyphen-Verfahren der Abbildungstrennung (polarisierte Gläser, Color-Code 3D, usw. ), die aber für unsere Zwecke nicht erforderlich sind, da sie vor allem zur Verbesserung der Farbdarstellung realer Bilder entwickelt wurden. Schauen wir uns mal an, was wir nun eigentlich erreichen wollen, d.h. wir definieren mal die Aufgabenstellung(en) und deren Lösung(en).
Aufgabe und Lösung I
Ein dreidimensionales Modell eines geometrischen Objektes wird durch Angabe seiner Eckpunkte (jeweils drei Koordinaten) und begrenzenden Kanten in einer Zeichenebene (also zweidimensional) definiert. Es entsteht ein "Drahtmodell", das die äußeren Konturen des Gegenstandes wiedergibt. (Also nochmals, das Modell wird nicht real dreidimensional gebaut, sondern in einer zweidimensionalen Ebene gezeichnet).
Dieser Gegenstand soll in ein Anaglyphenbild umgewandelt werden, das, betrachtet durch eine Rot/Cyan-Brille, den Gegenstand dreidimensional erscheinen lässt.
Lösung zu I
Tatsächlich abzubilden im Sinne einer optischen Abbildung sind lediglich die Eckpunkte des Modells. Wenn man die Kanten als Geraden zwischen je zwei Eckpunkten definiert, kann man nach der Berechnung der Bildpunkte die Kanten wieder als Geraden zwischen eben diesen Bildpunkten zeichnen. Eine Kante K[k] ist also ein Paar zweier Eckpunkte Gi ung Gj: K[k] := [i, j]. Die Eckpunkte seien von 1 bis N durchnummeriert (also 1 <= i, j <= N), die Kanten von 1 bis M (also 1 <= k <= M). Darüber hinaus vereinbaren wir, dass immer i < j ist, also keine leeren Kanten existieren und das Paar aufsteigende Eckpunktnummern hat: die Kante von Punkt 8 nach Punkt 3 wird also als [3, 8] geschrieben, was geht, da es keine gerichteten Kanten gibt. Dies bewirkt auch, dass keine Kante doppelt vorkommen kann.
Wie erfolgt nun die Abbildung eines Eckpunktes. Da ein Punkt durch 3 Koordinaten beschrieben ist, also einen räumlichen Bezug hat, gehen wir von zwei menschlichen Augen aus (L und R), die bei Betrachtung des Gegenstandes das Bild des Punktes auf ihrer Netzhaut haben. Diesen Bildpunkt kann man unter Festlegung gewisser geometrischer Größen näherungsweise über die einfache Konstruktion der optischen Abbildung (Abbildung 3 ff) berechnen; dabei soll die Regel, dass diese Konstruktion nur für Punkte nahe der optischen Achse annähernd korrekt ist, und die Linse (also die des Auges), die diese Abbildung erzeugt "dünn" ist, als erfüllt angesehen werden. Auch ist die Netzhaut keine euklidische Ebene, was wir ebenfalls vernachlässigen. Und der Vereinfachungen nicht genug, betrachten wir die gesamte Abbildung als in der Netzhautebene scharf, die Bildpunkte die vor oder hinter dieser Ebene entstehen, werden kurzerhand in die Netzhautebene projiziert. Damit sind die Koordinaten der Bildpunkte faktisch nur noch zweidimensional, jedenfalls liegen alle Bildpunkte des linken bzw. rechten Auges in jeweils einer Ebene, der jeweiligen Netzhaut des Auges. Soweit, so gut.
Wie entsteht nun das Anaglyphenbild, bis jetzt haben wir zwei unterschiedliche Bilder, die noch nicht übereinanderliegen? Ganz einfach, wir bilden die berechneten Bildpunkte wieder zurck auf eine BildBildebene ab, die im Bereich des eigentlichen Urgegenstandes liegt. Dadurch legen sich die beiden Bilder übereinander und es entsteht ein Anaglyphenbild, wenn wir die beiden Bilder verschiedenfarbig zeichnen.
Dies ist zweifelsohne ein stark vereinfachtes Verfahren, das an mehreren Stellen verbessert werden könnte. Aber die Ergebnisse sind recht brauchbar und darauf kam es mir zunächst einmal an. Die folgenden Beispiele zeigen zuerst immer das Urbild und dann die Stereographie, das gleiche Objekt auch in unterschiedlichen Blickrichtungen.
Weitere Beispiele

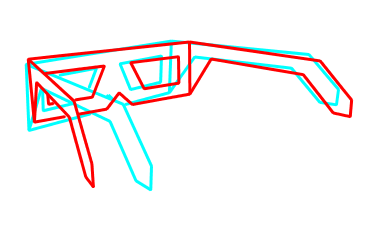
Die oben schon gezeigte Brille hier nun als Urbild und als Ansicht von der Seite.
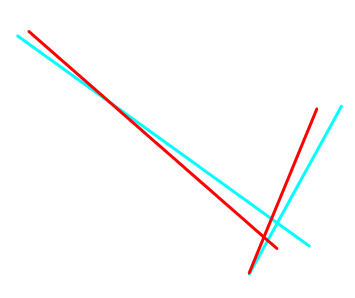
Als nächstes ein rein geometrisches Beispiel, zwei zueinander windschiefe Geraden. Bekanntlich können zwei Geraden im Raume nicht nur parallel sein oder sich schneiden, sondern auch weder das eine noch das andere tun: sie nennt man dann windschief zueinander.
Erst mal zwei Urbilder aus verschiedenen Blickwinkeln, dann zum ersten Urbild das Stereobild.


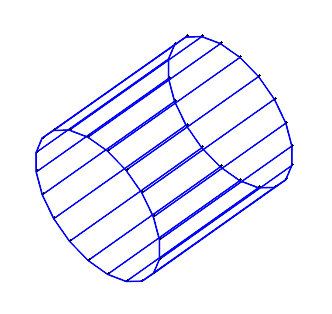
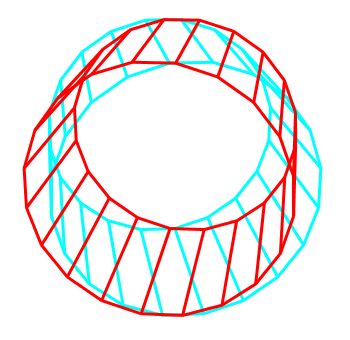
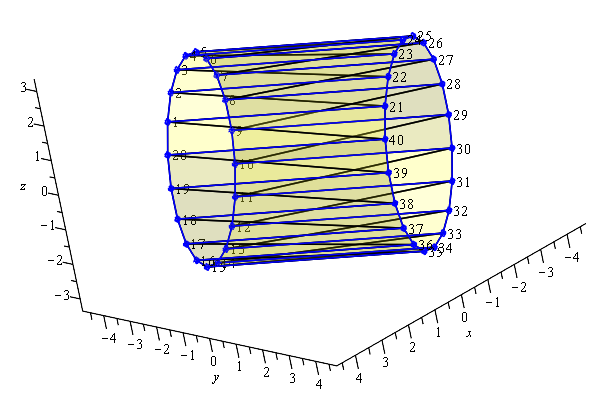
Da die Konstruktion des Urbildes auf Punkte und gerade Kanten beschränkt ist, muss die Darstellung eines Kreises oder allgemein krummliniger Figuren durch Polygonzüge angenähert werden. Das folgende Beispiel, ein Zylinder, hat als Boden und Deckel ein Zwanzigeck.

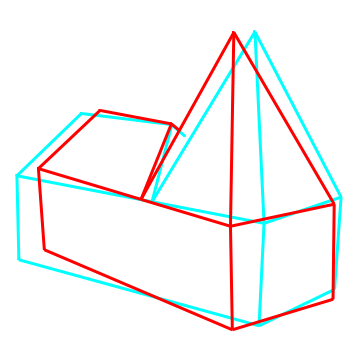
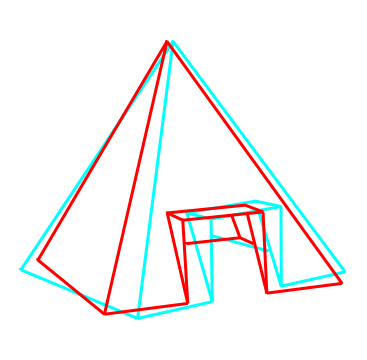
Das letzte Beispiel in dieser Reihe ist das Drahtmodell einer Kirche, das letztlich den Anlass gab, die zweite Aufgabenstellung zu formulieren und zu lösen; doch schauen wir uns erst mal die Bilder an.
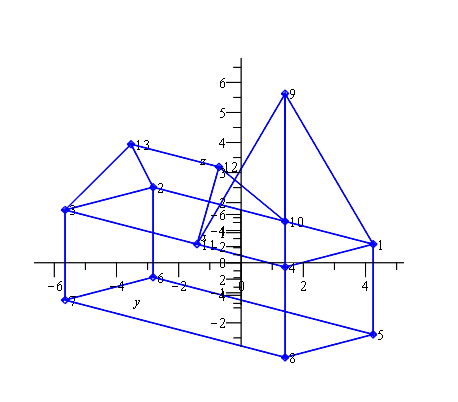
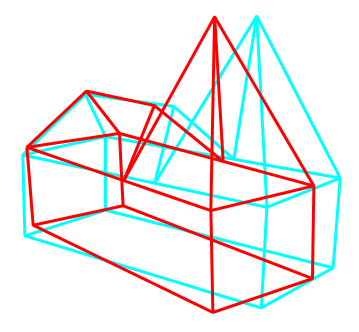
Zwar vermittelt auch hier das Anaglyphenbild einen dreidimensionalen Eindruck, aber in der Fülle der Kanten des Modells, ist die eigentliche Kontur nur schwer auszumachen, da sich die Kanten in der dreidimensionalen Darstellung letztlich auch zu schneiden scheinen. Dies wäre besser, wenn man vom reinen Drahtmodell zum Flächenmodell überginge, d.h., wenn es möglich wäre, in der Figur Flächen zu definieren, die zu einer Abdeckung dahinter liegender Strukturen führen würden. Um gleich zu zeigen, was ich meine, vorab schon mal eine Stereoprojektion der Kirche mit Flächen:
Der Eindruck mit Stereobrille ist deutlich ruhiger und vermittelt ein verständlicheres Bild des Gegenstandes, als das reine Drahtmodell. Doch nun die entsprechende Aufgabenstellung.
Aufgabe und Lösung II
Bei der Eingabe des Modells (Urbild) soll es möglich sein, von Kanten begrenzte Flächen zu definieren, die bei der Darstellung des Anaglyphenbildes dahinter liegende Teile des Modells unsichtbar machen (abdecken).
Lösung II
Die Eingabe der Flächen in ein (fertiges) Kantenmodell erfolgt in ähnlicher Weise wie bei den Kanten. Eine Fläche Fl(l) ist ein Tripel von drei unterschiedlichen Eckpunktnummern Gi, Gj und Gk, also (immer) ein Dreieck, das durch Kanten begrenzt sein kann (aber nicht muss). Also Fl(l) := [i, j, k] mit i < j < k. Die Flächen sind von 1 bis L durchnummeriert, also 1<= l <= L. Auch hier gilt, dass es keine leeren und auch keine doppelt vorkommenden Flächen gibt.
Bei der Berechnung des Anaglyphenbildes muss das Programm nun zusätzlich die gegenseitigen Lage der Eckpunkte, Kanten und Flächen berücksichtigen. Der notwendige Algorithmus ist programmtechnisch aufwändig und rechenzeitintensiv. Als grundlegende Idee sei folgendes vermerkt. Im ersten Schritt wird geprüft, ob durch die Flächen Eckpunkte abgedeckt werden, die dann aus der Liste der zu zeichnenden Punkte herausgenommen werden. Im zweiten Schritt prüft das Programm, ob ein Flächenstück eine Kante ganz oder teilweise abdeckt. Bei kompletter Abdeckung wird die Kante ebenfalls aus der Liste zu zeichnender Kanten entfernt; bei teilweiser Abdeckung ist die Situation schwieriger. Hier wird durch Hinzufügen "virtueller" Eckpunkte und Kanten ein Modell geschaffen, das nur noch die sichtbaren und damit zu zeichnenden (neuen und alten) Punkte und (neuen und alten) Kanten enthält. Die neuen Eckpunkte liegen an den Stellen, wo alte Kanten hinter eine Fläche eintreten oder aus ihr austreten. Die neuen Kanten stellen dann die sichtbaren Verbindungen der alten und neuen Eckpunkte dar. Um diese Ein- und Austrittsstellen zu finden wird für jede Kante und jede Fläche mit minimaler Schrittweite, quasi Pixel für Pixel, die Lage geprüft.
Bei der Entscheidung, wie die Flächen zur definieren seien, kann ich mir nachträglich nur dazu gratulieren, dass ich nur Dreicksflächen zur Eingabe zugelassen habe und nicht, wie ich zunächst plante, ein beliebiges n-Eck. Die Vereinfachungen bei der Realisierung, die das mit sich brachte, haben den Erfolg erst möglich gemacht. Ohne dies wäre mir letztlich nur übrig geblieben, das n-Eck selber zu triangulieren, was allein schon kein einfaches Problem ist. So muss der Anwender dies nur bei der Eingabe selber machen, was aber durch vielseitige Unterstützung des Programmes relativ leicht möglich ist.
Betrachten wir auch hier nun ein paar Beispiele.
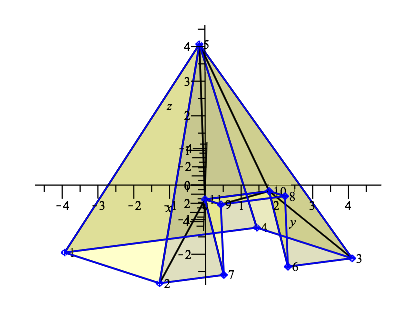
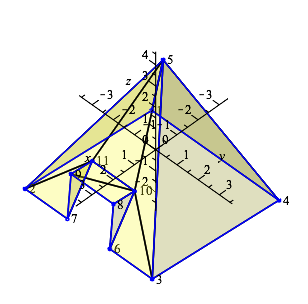
Als erstes kehren wir zu der oben schon gezeigten Kirche zurück, für die nun noch das Urbild mit den Flächen aussteht.
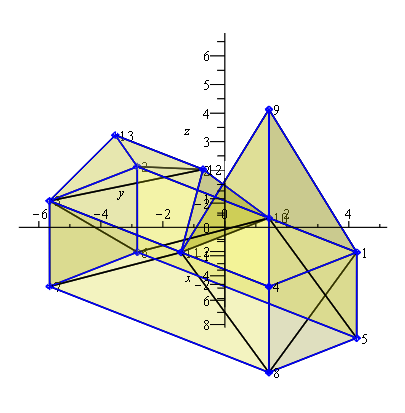
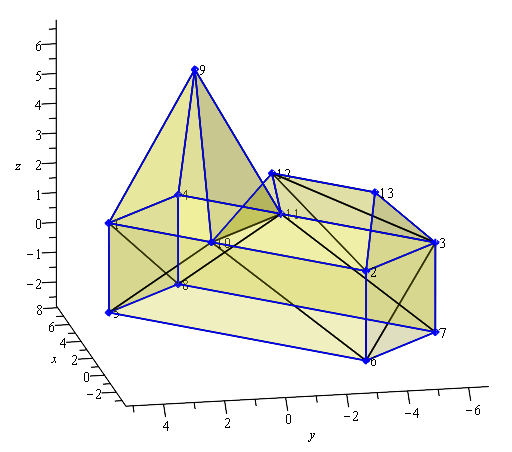
Die Flächen des Modells sind in dunkelgelber Farbe halbtransparent dargestellt, die realen Kanten des Modells in blau, zusätzliche Begrenzungen der Dreiecksflächen in schwarz. Der Boden der Kirche wurde nicht mit 2 Flächen belegt, da er bei Betrachtung von oben ohnehin unsichtbar ist, also andererseits keine Punkte oder Kanten abdecken kann. Sollte man die Kirche von unten betrachten wollen, so müsste man sie noch nachtragen oder man sieht in das Innere der Kirche.
Auch die am Anfang schon einmal gezeigte Brille in Abbildung 8 hat schon Flächen, der linke Bügel deckt Teile des Rahmens der Brille ab.
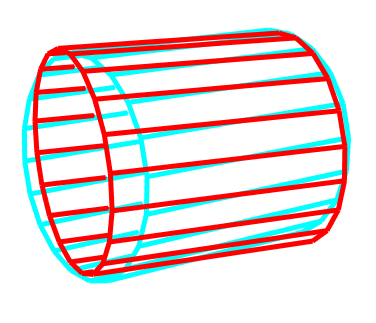
Lassen wir nun den Zylinder als Röhre erscheinen, also den Mantel mit Flächen abdecken.
Programm zur Realisierung
Auch ein Subsystem zum Schreiben und Lesen von Dateien (für die Eckpunkte, Kanten und Flächen) ist bei Maple vorhanden.
Das Programm "Draht3D" besteht aus folgenden Hauptkomponenten:
- Berechnung der Optischen Abbildungen für Bild und BildBild (ca. 5%)
- Grafische Aufbereitung und Ausgabe des Urbildes in 3D und des Anaglyphenbildes in 2D (ca. 5%)
- Berechnung der Abdeckung von Eckpunkten und Kanten durch Flächen (ca. 15%)
- Anwenderdialog zur Eingabe und Verwaltung der Urbilder und der Steuerung des Ablaufes (ca. 73 %)
- Verwaltungs- und Testroutinen (ca. 2%)
Typisch! Der Anwender soll es komfortabel haben, dies nimmt den weitaus größten Umfang des Programmmcodes ein.
Wer das Programm selber benutzen möchte, kann es für private Zwecke oder für die Unterstützung der Lehre gerne verwenden. Eine ausführliche Beschreibung und Bedienungsanleitung, sowie das Programm selber werde ich in der nächsten Version dieser Webseite veröffentlichen.
Wer es nutzen will, benötigt allerdings eine moderne Maple-Version, ich habe es mit der Version 17 entwickelt und mit Maple 2015 getestet. Wie weit zurück man mit den Versionen gehen kann, weiß ich nicht, sicher ist aber, dass es mit Version 9 nicht mehr läuft; zugegeben eine sehr grobe Abschätzung, aber ich besitze dazwischen keine weiteren Versionen.
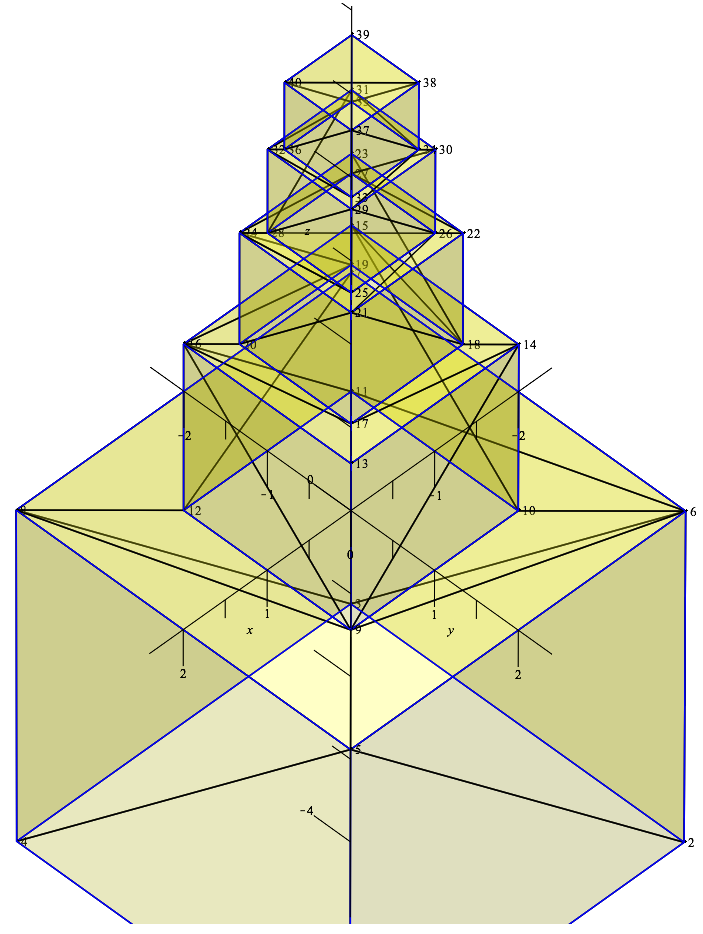
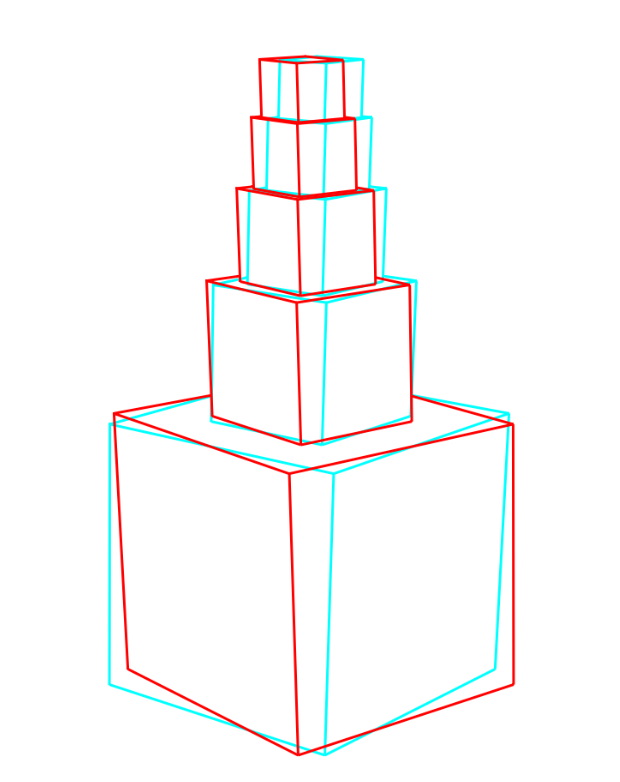
Zum Abschluss ein letztes Beispiel; in den "Aufgaben und Lösungen" auf dieser Webseite habe ich den Turmbau zu Babylon als Beispiel für unendlichen Summen verwendet. (Die Seitenlänge beginnt beim untersten Würfel mit 1, der nächsthöhere hat 1/2, dann 1/3, 1/4 und 1/5) Hier will ich jetzt den Turm, allerdings nur bis zur Höhe 5, als dreidimensionales Bild zeigen: