

- Will ich oder will ich nicht?
- 0 Graphen in Wort und Bild
- 1 Graphen und Mathematik
- 1.1 Adjazenz, Inzidenz, Laplace und Grad
- Ausflug in die Lineare Algebra
- Fortsetzung 1.1
- 1.2 Spektral Layout
- 1.3 Der Zufallswanderer
- 1.4 Gleichstromkreise als Graphen
- 2 Von v nach w, Wege durch Graphen
- 2.1 Der Nikolaus in Königsberg
- 2.2 Kurz und knapp
- 3 Man sieht den Wald vor Bäumen nicht
- 3.1 Zu bunt?
- 3.2 Unter Spannung
- 4 Panta rei - Alles fließt
- 4.1 Nichts wie raus!
- 4.2 Wer mit wem?
- 5 Und sonst?
- 5.1 Wahr - scheinlich
- 5.2 Bäumchen wechsel Dich
- 5.3 Nach Adam Riese
- 6 Das Beste kommt zum Schluss
- Literaturverzeichnis
Wenn der Graph lacht
Will ich oder will ich nicht?
Beim Durchforsten des Internet, von Aufsätzen und Büchern (natürlich ohne den geringsten Anspruch auf Vollständigkeit) zeigt sich nicht nur die Vielfalt der Anwendungen der Graphen in anderen Bereichen der Mathematik, der Informatik, der Naturwissenschaften und Technik, neuerlich als MINT-Fächer bezeichnet, sondern auch im täglichen Leben. Bei dieser Durchforstung fällt aber auch auf, dass die Graphentheorie selber eine Fülle von Begriffsbildungen hat und, dass diese leider nicht sehr einheitlich definiert sind. Das führt oft zu Verwirrung und damit zu Verständnisschwierigkeiten, denn nichts ist beim Lernen schlimmer, als Vorstellungen, die man mit einem bestimmten Begriff verbindet, mal so und mal anders assoziieren zu müssen und gerade in der Mathematik kommt es ja oft auch auf Kleinigkeiten an.
Will ich nun oder will ich nicht?
Keine Frage, sonst hättet Ihr ja diesen Post nicht auf meiner Seite gefunden; viel wichtiger ist die Frage: "Was will ich denn?" Ich glaube, es hat in diesem Fall keinen Zweck, ein anderes Ziel anzustreben, als die Vielfalt dieser Theorie und ihrer Anwendungen ausschnittsweise darzustellen; das will ich versuchen.
Ach ja, ich schreibe Graph nach wie vor mit "ph" und nicht mit "f", um mich nicht der Frage auszusetzen, was ich mache, wenn der Graf stirbt ...
0 Graphen in Wort und Bild
Bemerkung: Beim MouseOver über eine Abbildung erscheint eine kurze Beschreibung.


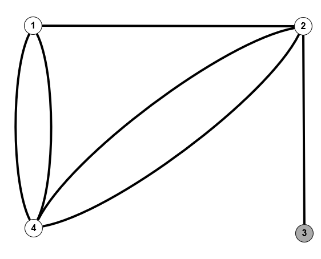
Vielfach kommen auch Mischformen vor, z.B. gerichtete Mulitigraphen oder gewichtete Bäume oder, oder, oder...
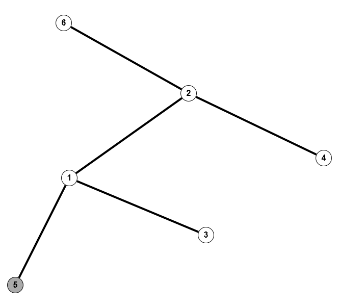
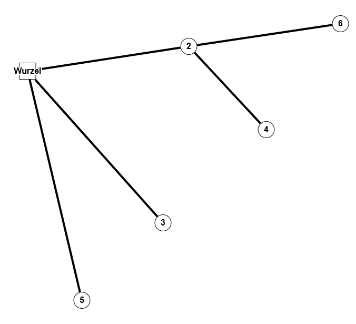
Auch die Anordnung von Knoten und Kanten kann zu speziellen Typen von Graphen führen, beispielsweise bipartite Graphen, Graphen mit isolierten Knoten oder Graphen mit mehreren Zusammenhangskomponenten oder Graphen, die als Wald oder Baum bezeichnet werden (siehe Bildkommentare):

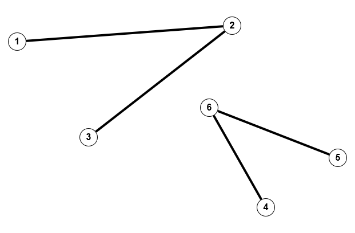
Was macht man mit Graphen? Die Antwort auf diese Frage ist mindestens so vielfältig, wie die unterschiedlichen Graphentypen. Ein großer Bereich von Anwendungen wird in der Informatik behandelt, was dann meistens mit Algorithmen verbunden ist, die bestimmte, konkrete Probleme lösen sollen. Schlagworte an dieser Stelle sind Heiratsproblem, kürzeste Wege, Travelling Salesman, Spieltheorie. Aber auch in der Mathematik werden Graphen nicht nur zur Visalisierung eingesetzt, sondern auch zur Problemlösung und Beweisführung.
Aber jeder Autor, der Graphentheorie verwenden will, macht sich seine eigenen Definitionen und Sätze und benutzt nur den Teil dieser Theorie, den er braucht und biegt die Begriffe, wie schon oben erwähnt so hin, dass sie ihm passen. Zugegeben eine rein abstrakte Behandlung von Graphen ist auf die Dauer langweilig, wo sich doch gerade hier die Visualisierung anbietet.
Sei es, wie es sei. Ich will versuchen, einen guten Mittelweg in der Theorie zu finden und natürlich die Anwendungen nicht vernachlässigen.
1 Graphen und Mathematik
Kardinalität
Sei $M$ eine Menge. Dann bedeutet $|M|$ die Anzahl der Elemente von $M$. Wir setzen $|M|=\infty$ wenn $M$ nicht endlich ist.
Potenzmenge
Sei $M$ eine Menge. Dann heißt:
$\mathfrak{P}(M)=\{A | A \subseteq M\}$ die Potenzmenge von M, also die Menge aller Teilmengen von $M$ und
$\mathfrak{P}_k(M) = \{A | A\subseteq M, \; |A| = k \}$ die Menge aller k-elementigen Teilmengen von $M$.
Beachte: $\{a,b\} = \{b,a\} = \{a,b,a\} = \{b,b,a\}$.
Kartesisches Produkt
Seien $A$ und $B$ Mengen. Dann heißt:
$A \times B =\{(a,b) | a \in A, \; b \in B \}$ das kartesische Produkt von $A$ und $B$, also die Menge aller geordneten Paare, die man aus $A$ und $B$ bilden kann.
Beachte: $(a,b) \neq (b,a)$.
Relation
Eine Relation $R$ ist eine Teilmenge eines kartesischen Produktes: $R \subseteq A \times B$.
Äquivalenzrelation
Eine Äquivalenzrelation ist eine Relation auf einer Menge $M$, die reflexiv ($\forall x \in R: (x,x) \in R$), symmetrisch ($ \forall x,y \in R: (x,y) \in R \Rightarrow (y,x) \in R$) und transitiv ($\forall x,y, z \in R: (x,y) \in R \wedge (y,z) \in R \Rightarrow (x,z) \in R$) ist.
Eine Äquivalenzklasse ist eine Teilmenge von $M$, die aus allen zu einem festen Element $x \in M$ äquivalenten Elementen besteht: $[x] = \{y \in M | (x,y) \in R\}$. Die Äquivalenzklassen bilden eine Zerlegung von $M$, d.h. $M$ ist gleich der disjunkten Vereinigung aller Äquivalenzklassen.
Natürliche Zahlen
$\mathbb{N} = \{1, 2, 3, \dots \}$
$\mathbb{N}_0 = \{0, 1, 2, 3, \dots \}$
$\mathbb{N}_k = \{1, 2, 3, \dots, k\}, \; k \neq 0 $
Definition 1.1 (Graph, Knoten, Kante)
Ein Graph $G$ ist ein geordnetes Paar $(V,E)$ aus einer Menge $V$, den Knoten (Vertex) und einer Menge $E$, den Kanten (Edge). Ist $V$ leer, dann spricht man von einem leeren Graphen.
Dabei unterscheidet man folgende Typen von Graphen:
Ungerichteter Graph ohne Mehrfachkanten
$E \subset \mathfrak{P}_2(V) $, E besteht also aus 2-elementigen Mengen, die jeweils eine Kante darstellen.
Gerichteter Graph ohne Mehrfachkanten
$E \subset V \times V$, E besteht also aus geordneten Paaren, die jeweils eine Kante darstellen und eine Orientierung haben.
Ungerichteter Graph mit Mehrfachkanten (ungerichteter Multigraph)
$E: \mathfrak{P}_2(V) \rightarrow \mathbb{N}_0$, E besteht also aus ungerichteten Kanten verbunden mit einer Vielfachheit aus $\mathbb{N}_0$.
Beachte: Eine Abbildung ist eine Relation und damit auch eine Menge!
Gerichteter Graph mit Mehrfachkanten (gerichteter Multigraph)
$E: V \times V \rightarrow \mathbb{N}_0$, E besteht also aus gerichteten Kanten verbunden mit einer Vielfachheit aus $\mathbb{N}_0$.
Ende der Definition 1.1.
Diese häufig zu findende Definition hat den Nachteil, dass ihre formale Korrektheit erst durch die Defintion der 4 spezielle Typen hergestellt wird. Die Definition lässt zu, dass $V = \{1,2,4\}$ und $E=\{4\}$, was sicher keinen sinnvollen Graphen ergibt. Deshalb ist es besser, gleich eine übergreifende Beschreibung zu verwenden, die alle Fälle abdeckt und dann spezialisiert wird. Dies leistet:
Definition 1.1'
Ein Graph $G$ ist ein geordnetes Paar $(V,\mathfrak{E})$ aus einer Menge $V$, den Knoten (Vertex) und einer (Kanten-)Abbildung $\mathfrak{E}: V \times V \rightarrow \mathbb{N}_0$.
$e=(u,v) \in V \times V$ heißt Kante von $G$, wenn $\mathfrak{E}(u,v) > 0$ und Mehrfachkante, wenn $\mathfrak{E}(u,v) > 1$.
Die Kantenmenge ist definiert als $E := \{(u,v) | \mathfrak{E}(u,v) > 0\}$.
Ende der Definition 1.1'.
1.1' entspricht zunächst der des gerichteten Graphen mit Mehrfachkanten, ist aber so allgemein, dass man die oben genannten 4 Spezialfälle einordnen kann.
$G$ heißt ungerichtet, wenn für alle Knoten $u,v \in V $ gilt: $\mathfrak{E}(u,v) = \mathfrak{E}(v,u)$. Dann spielt die "Richtung" einer Kante keine Rolle und man kann statt $\mathfrak{E}: V \times V \rightarrow \mathbb{N}_0$ auch $\mathfrak{E}: \mathfrak{P}_2(V) \rightarrow \mathbb{N}_0$ schreiben.
$G$ heißt ohne Mehrfachkanten, wenn für alle $u,v \in V$ gilt: $\mathfrak{E}(u,v) \leq 1$. In diesem Fall ist die Kantenmenge $E = \{(u,v) | \mathfrak{E}(u,v) = 1\} $ und man kann $E$ als Teilmenge von $ V \times V $ betrachten. (Genauer: man kann die Abbildung $\mathfrak{E}$ mit der Menge $E$ über die "charakteristische Funktion" identifizieren.)
Durch Mischung erhält man alle 4 oben definierten Fälle.
Für den häufigen Fall eines ungerichteten Graphen ohne Mehrfachkanten, kann man letztlich $E$ als Teilmenge von $\mathfrak{P}_2(V)$ auffassen.
(Ganz viele) Schreibweisen und Bezeichnungen:
$V=V(G)$ und $E=E(G)$
$e \in E, e=\{v,w\}$, dann heißen $v$ und $w$ Endknoten, $e=(v,w),$ dann heißt $v$ Startknoten, $w$ Endknoten, $e=(v,v)$ oder $e=\{v\}$ dann heißt $e$ Schleife.
Ein ungerichteter Graph ohne Mehrfachkanten und Schleifen heißt einfach (oder auch schlicht).
$n(G):= |V(G)| = $ Anzahl der Knoten in $G$, auch Ordnung von $G$ genannt, diese kann auch Unendlich sein.
$m(G):= |E(G)| = $ Anzahl der Kanten von G (bei Multigraphen gemäß Vielfachheit).
Ein isolierter Knoten $v \in V$ kommt in keiner Menge bzw. in keinem Paar von E vor.
Zwei Knoten $v,w \in V$ in einem ungerichteten Graphen heißen benachbart (oder adjazent oder sind Nachbarn), wenn $\mathfrak{E}(v,w) > 0$. Die zugehörige Kante $e \in E$ heißt inzident zu v und w. Ein isolierter Knoten ist zu keiner Kante inszident.
In einem gerichteten Graphen heißt $v$ Vorgänger von $w$ ($w$ Nachfolger von $v$), wenn $e=(v,w)$ eine gerichtete Kante ist.
Sei $G$ ein ungerichteter Graph, $v \in V$; dann definieren wir:
$d_G(v) := $ Summe der Vielfachheiten der benachbarten Kanten; wenn $G$ keine Mehrfachkanten hat, entspricht dies der Anzahl der benachbarten Knoten.
$d_G(v)$ heißt Grad des Knoten $v$.
$\delta(G) := min \{d_g(v)|v \in V\}$ Minimalgrad von $G$.
$\Delta(G) := max \{d_g(v)|v \in V\} $ Maximalgrad von $G$.
$d(G) := \frac{\sum_{v \in V} d_G(v)}{n(G)}$ Durchschnittsgrad von $G$.
Bemerkung
Es gilt: $d(G) = 2 \cdot m(G) / n(G)$.
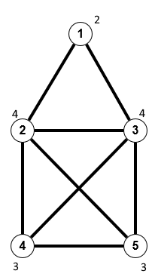 Grade des Graphen: $\delta(G) = 2, \; d(G) = \frac{16}{5}, \; \Delta(G) = 4$
Grade des Graphen: $\delta(G) = 2, \; d(G) = \frac{16}{5}, \; \Delta(G) = 4$$G$ heißt regulär, wenn alle Knoten den gleichen Grad haben, k-regulär, wenn der gemeinsame Grad k ist.
Beobachtung 1.2
$\delta(G) \leq d(G) \leq \Delta(G)$. Wenn $G$ regulär, gilt Gleichheit.
Satz 1.3
Sei $G$ ein (endlicher) ungerichteter Graph. Die Anzahl der Knoten mit ungeradem Grad ist gerade.
Beweis_1_3.pdf
Sei $G$ ein gerichteter Graph, $v \in V$; dann definieren wir:
$d_G^-(v) :=$ Anzahl der Vorgänger von $v$, wenn $G$ keine Mehrfachkanten hat (Ausgangsgrad).
$d_G^-(v) :=$ Summe der Vielfachheiten aller Kanten in $G$ mit $v$ als Startknoten (also (v,x)), wenn $G$ Mehrfachkanten hat.
$d_G^+(v) :=$ Anzahl der Nachfolger von $v$, wenn $G$ keine Mehrfachkanten hat (Eingangsgrad).
$d_G^+(v) :=$ Summe der Vielfachheiten aller Kanten in $G$ mit $v$ als Endknoten (also (x,v)), wenn $G$ Mehrfachkanten hat.
$v$ Quelle $:\Leftrightarrow d_G^- = 0, v$ Senke $:\Leftrightarrow d_G^+ = 0$.
$v$ isoliert $:\Leftrightarrow d_G^-(v) = d_G^+(v)=0$.
Ein endlicher Graph liegt vor, wenn $|V| < \infty$. Dann ist auch die Kantenmenge endlich und dies auch in Multigraphen, da die Vielfachheitsabbildung $\mathfrak{E}$ laut Definition nicht den Wert Unendlich annimmt (Kontengrad ist immer endlich).
Alle Graphen dieses Aufsatzes sind als endlich vorausgesetzt.
Definition 1.3a (Kantengewichtsfunktion)
Sei $G=(V,E)$ ein (gerichteter oder ungerichteter) Graph. Eine Kantengewichtsfunktion ist eine Abbildung der Form
$$g: E \rightarrow \mathbb{R}$$
g(e) ist dann eine reelle Zahl und wird Kantengewicht genannt
Beispiele und Missverständnisse
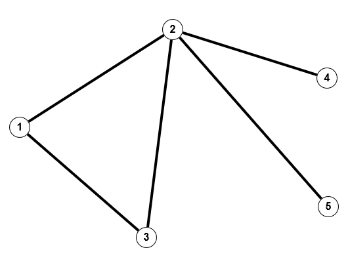
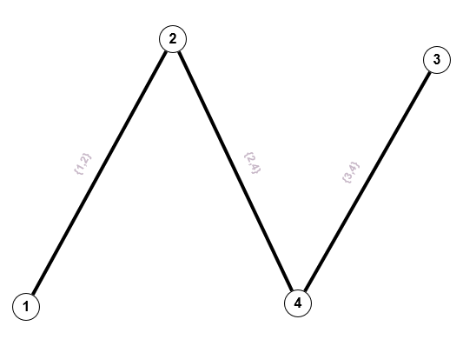 $V = \mathbb{N}_4 = \{1,2,3,4\}, \; E=\{\{1,2\},\{2,4\},\{3,4\}\}$
$V = \mathbb{N}_4 = \{1,2,3,4\}, \; E=\{\{1,2\},\{2,4\},\{3,4\}\}$ausgeräumte Missverständnisse
- Ein Graph kann isolierte Knoten haben, d.h. Knoten, die weder Anfangspunkt noch Endpunkt einer Kante sind.
- Sowohl die Knotenmenge als auch die Kantenmenge kann unendlich viele Element haben.
- Ein Graph muss nicht zusammenhängend sein (Definition siehe unten).
- Das Überkreuzen zweier Kanten an sich ist bedeutungslos.
- Die Winkel zwischen den Kanten haben keine Bedeutung.
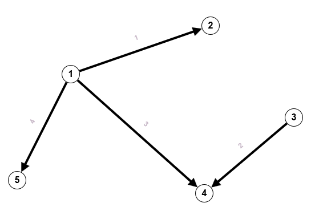
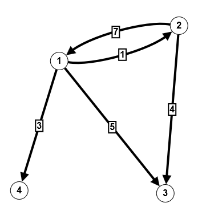
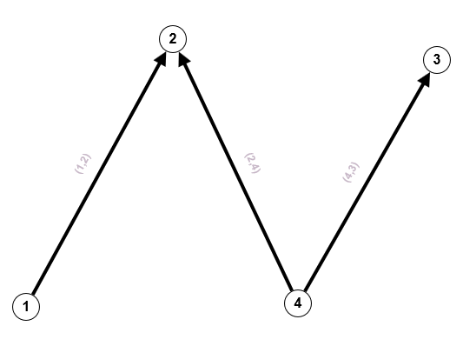 $V = \mathbb{N}_4 = \{1,2,3,4\}, \; E=\{(1,2),(2,4),(4,3)\}$
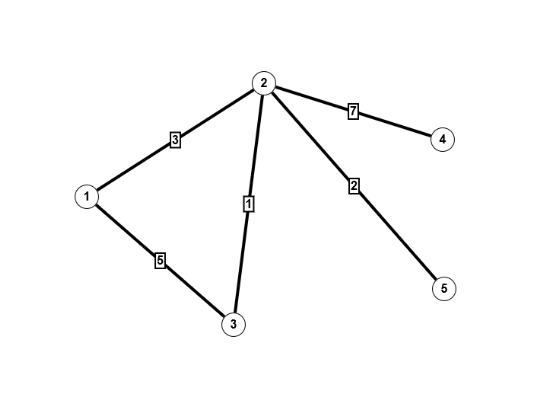
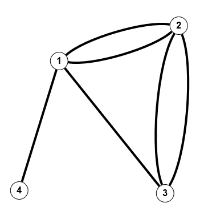
$V = \mathbb{N}_4 = \{1,2,3,4\}, \; E=\{(1,2),(2,4),(4,3)\}$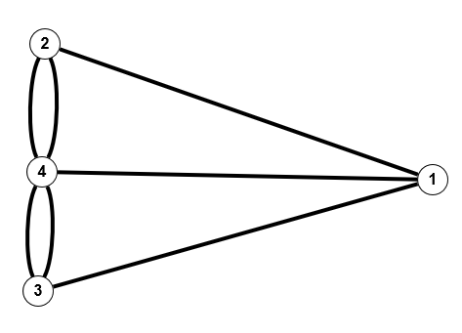 $V = \mathbb{N}_4, \; E=\{(\{1,2\},1),(\{1,3\},1),(\{1,4\},1),(\{2,4\},2),(\{3,4\},2)\}$
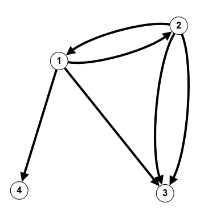
$V = \mathbb{N}_4, \; E=\{(\{1,2\},1),(\{1,3\},1),(\{1,4\},1),(\{2,4\},2),(\{3,4\},2)\}$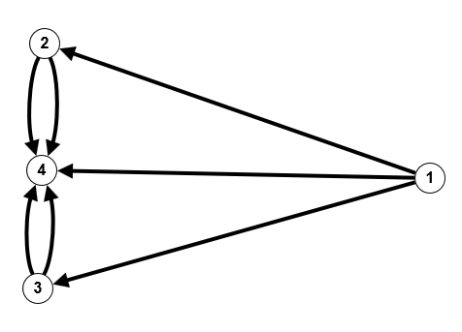 $V = \mathbb{N}_4, \; E=\{((1,2),1),((1,3),1),((1,4),1),((2,4),2),((3,4),2)\}$
$V = \mathbb{N}_4, \; E=\{((1,2),1),((1,3),1),((1,4),1),((2,4),2),((3,4),2)\}$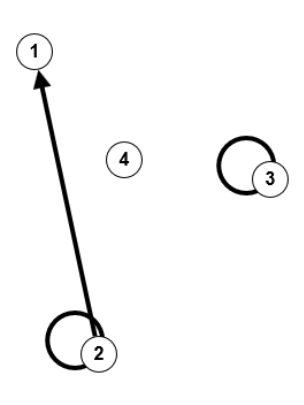 $V = \mathbb{N}_4, \; E=\{(2,1),(2,2),(3,3)\}$
$V = \mathbb{N}_4, \; E=\{(2,1),(2,2),(3,3)\}$Ausgeräumte Missverständnisse
- Schleifen können sowohl in ungerichteten als auch in gerichteten Graphen vorkommen, werden aber meisten nur in gerichteten Graphen betrachtet.
- Pro Knoten gibt es nur eine Schleife.
Es lassen sich Zusammenhänge zwischen den unterschiedlichen Graphentypen herstellen, genauer, man kann Typen aufeinander zurückführen.
- Ein ungerichteter Graph kann durch einen gerichteten Graphen ersetzt werden, indem jede ungerichtete Kante in zwei gegeneinander gerichtete Kanten zwischen den gleichen Knoten aufgelöst wird. $\{v,w\} \rightarrow (v,w), (w,v)$. Auf diese Weise kann man auch einen Graphen verstehen, in dem ungerichtete und gerichtete Knoten gemischt auftreten.
- Ein Multigraph kann in einen Graphen ohne Mehrfachkanten umgewandelt werden, indem man alle Kanten zwischen zwei Knoten bis auf eine durch einen pro Kante zusätzlich eingefügten Knoten unterteilt. $ \{v,w\}$ mit $E(\{v,w\}) = 2 \rightarrow \{v,w\} , \; \{v,v'\}, \; \{v',w\}$.
- Nimmt man 1 und 2 zusammen, so könnte man eigentlich nur gerichtete Graphen ohne Mehrfachkanten betrachten, aber vielfach ist es einfacher, doch alle definierten Typen zu verwenden.
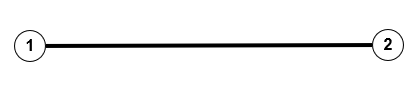
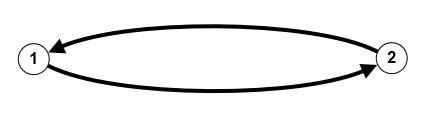
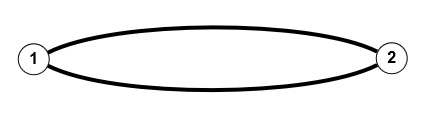
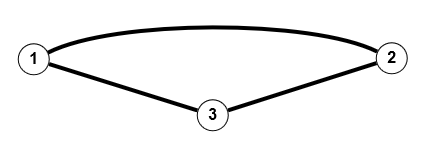
Spezielle Graphen sind:
$K_n$ : der vollständige Graph auf $\mathbb{N}_n, \; n \in \mathbb{N}$, d.h. $V(K_n) = \mathbb{N}_n$ und $E(K_n) = \mathfrak{P}_2(\mathbb{N}_n)$. Somit ist $K_n$ ungerichtet, ohne Mehrfachkanten und ohne Schleifen.
Beobachtung 1.4
Jeder vollständige Graph ist regulär.
$C_n$: der Kreis-Graph oder einfach Kreis auf $\mathbb{N}_n, \; n \in \mathbb{N}, \; n \geq 3$, d.h. $V(C_n) = \mathbb{N}_n$ und $E(C_n) = \{\{i,i+1\}|1 \leq i \leq n-1\} \cup \{\{n,1\}\}$
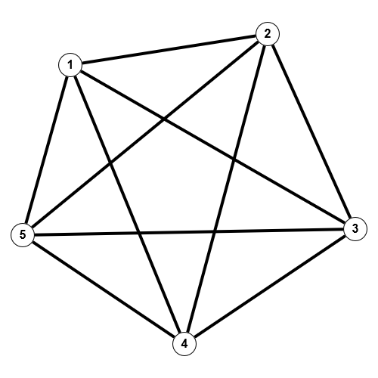 $K_5$
$K_5$ 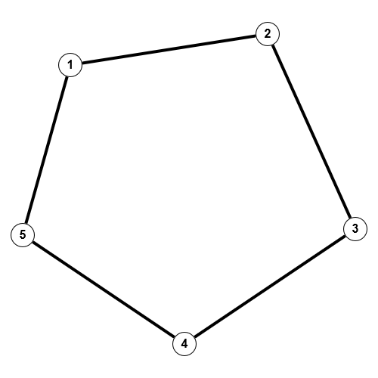 $C_5$
$C_5$Und nun zur zweiten zentralen Definition dieses Kapitels. Man kann Graphen auf verschiedene Art und Weise zeichnen, nicht nur mit unterschiedlichen Bezeichnungen, unterschiedliche Anordnung der Knoten und Kanten usw. Deshalb muss man definieren, wann Graphen in einer bestimmten Weise "gleich" sind, der definierte Begriff heißt "isomorph".
Definition 1.5
Zwei ungerichtete Graphen $G=(V,E), G'=(V',E')$ heißen isomorph $(G \cong G')$, falls eine bijektive Abbildung $f:V \rightarrow V'$ gibt mit:
$$ \forall v,w \in V: \{v,w\} \in E \Leftrightarrow \{f(v),f(w)\} \in E'. $$
Entsprechendes definiert man für gerichtete Graphen mit Paaren statt mit 2-elementigen Mengen bzw. für Multigraphen. Bei Multigraphen ist es einfacher zu schreiben $E(\{v,w\})=E'(\{f(v),f(w)\})$ für ungerichtete und $E((v,w))=E'((f(v),f(w)))$ für gerichtete Multigraphen.
Definition 1.5' (auf der Basis der Definition 1.1')
Zwei Graphen $G=(V,\mathfrak{E}), G'=(V',\mathfrak{E'})$ heißen isomorph $(G \cong G')$, falls eine bijektive Abbildung $f:V \rightarrow V'$ gibt mit:
$$\forall v,w \in V: \mathfrak{E}(v,w) = \mathfrak{E'}(f(v),f(w)).$$
Sofern die Graphen Kantengewichtsfunktionen haben, dann müssen für Isomorphie korrespondierende Kanten auch das gleiche Gewicht haben.
Betrachten wir als Beispiel den obigen vollständigen Graphen und einen weiteren:
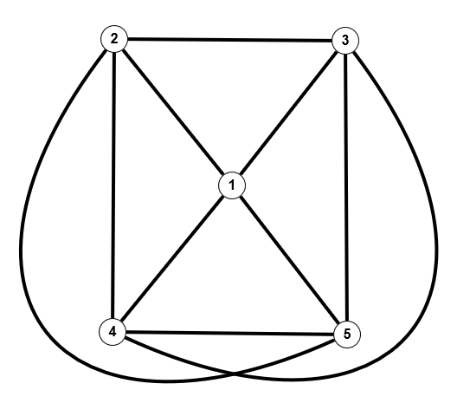
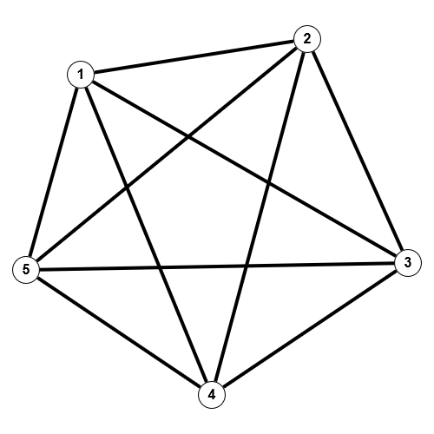
Sind diese beiden Graphen isomorph? Auf den ersten Blick findet man keine große Ähnlichkeit zwischen den beiden Bildern, außer vielleicht, dass beide eben vollständig sind. Aber folgende Abbildung $f$ zeigt die Isomorphie:
$G=(V,E), \; G'=(V',E'), \; V=V'=\mathbb{N}_5, \; E=E'=\{\{1,2\},\{1,3\},\{1,4\},\{1,5\},\{2,3\},\{2,4\},\{2,5\},\{3,4\},\{3,5\},\{4,5\}\}$ und $f = id_V$.
Tatsächlich sind zwei vollständige Graphen gleicher Knotenzahl $(n(G)=n(G'))$ immer auch isomorph.
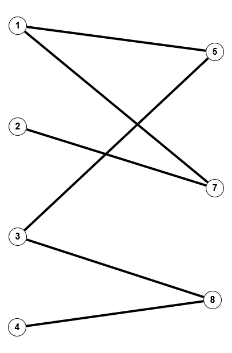
Aber auch ohne Vollständigkeit gibt es isomorphe Graphen, wie das zweite Beispiel [1] zeigt.

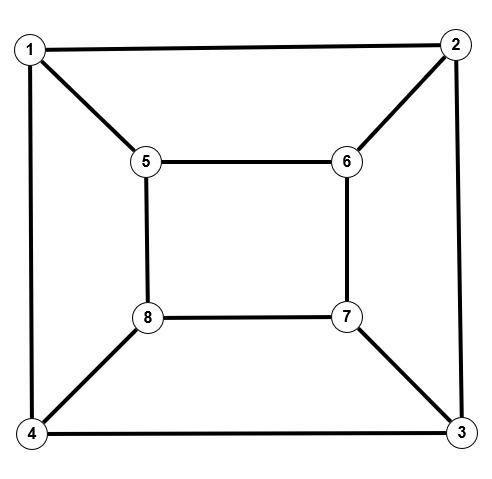
$P=(V,E), \; P'=(V',E'), \; V=\{A,B,C,D,E,F,G,H\}, \; V'=\{1,2,3,4,5,6,7,8\}$
$E=\{\{A,B\}, \{A,D\},\{A,F\},\{B,C\},\{B,E\},\{C,D\},\{C,H\},\{D,G\},\{E,F\},\{E,H\},\{G,G\},\{G,H\}\}$
$E'=\{\{1,2\},\{1,4\},\{1,5\},\{2,3\},\{2,6\},\{3,4\},\{3,7\},\{4,8\},\{5,6\},\{5,8\},\{6,7\},\{7,8\}$
$f(A)=1, \; f(B)=6, \;f(C)=8, \;f(D)=3, \;f(E)=5, \;f(F)=2, \;f(G)=4, \;f(H)=7$
Bemerkung 1.6
Die beiden obigen Graphen haben, wie wir später noch definieren werden, eine bestimmte Struktur, die man "bipartit" nennt. Bei dem linken Graphen $P$ erkennt man dies sofort.
Satz 1.7
Die Isomorphie $\cong$ zweier Graphen $G=(V,E), G'(V',E')$ ist auf der Menge ungerichteter, einfacher Graphen mit gleicher, endlicher Mächtigkeit der Knotenmenge $(n(V)=n(V'))$ eine Äquivalenzrelation.
Somit gibt es eine Zerlegung in Äquivalenzklassen pro $n(V)$. Folgendes Beispiel zeigt den Fall $n=3$, für $V=\mathbb{N}_3$, wobei es auf die Knotenbezeichungen nicht ankommt.
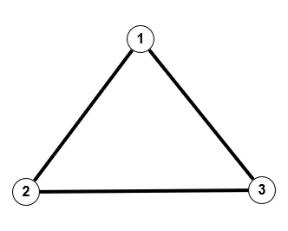 Äquivalenzklasse mit 3 Kanten
Äquivalenzklasse mit 3 Kanten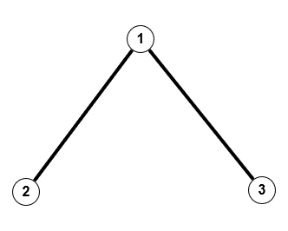

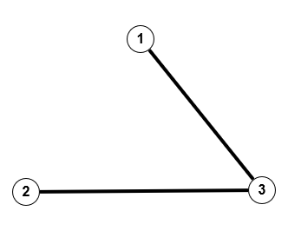 Äquivalenzklasse mit 2 Kanten
Äquivalenzklasse mit 2 Kanten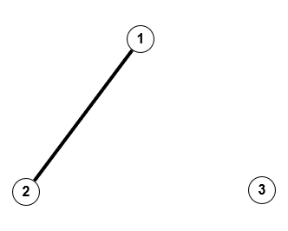
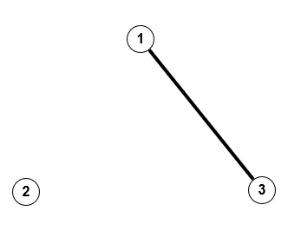
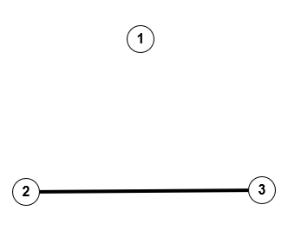 Äquivalenzklasse mit 1 Kante
Äquivalenzklasse mit 1 Kante Äquivalenzklasse ohne Kante
Äquivalenzklasse ohne Kanteausgeräumte Missverständnisse
Man könnte aufgrund dieses Beispiels vermuten, dass immer Graphen mit gleicher Kantenzahl eine Äquivalenzklasse bilden. Dies ist nicht so, wie man an folgendem Beispiel für $n=4$ sieht. Die beiden Graphen haben die gleiche Kantenzahl (bei gleicher Knotenmenge), sind aber nicht isomorph.
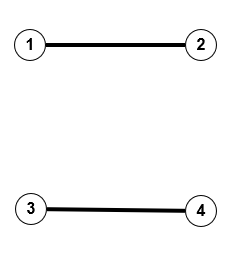

Für den Nachweis, dass zwei gegebene Graphen isomorph sind, ist kein Algorithmus bekannt, der das in polynominaler Zeit schaffen würde. [1] Ebenso ist die Frage, wie viele Äquivalenzklasse es bei gegebenem Graphen $G$ gibt, schwierig zu beantworten. [2] Aber immerhin weiß man:
Satz 1.8
(a) $|\mathfrak{P}_2(\mathbb{N}_k)| = \binom{k}{2}$, was bedeutet, dass ein einfacher Graph mit $k$ Knoten höchstens $\frac{k(k-1)}{2}$ Kanten haben kann.
(b) Es gibt $2^{\binom{k}{2}}$-viele Graphen $G$ mit $V(G) = \mathbb{N}_k$, also $|V(G)| = k$.
(c) Der vollständige Graph $K_n$ hat $\frac{n(n-1)}{2}$ Kanten (folgt direkt aus a).
Zum Abschluss dieses Kapitels noch vier Definitionen für spätere Verwendung.
Definition 1.9 [9]
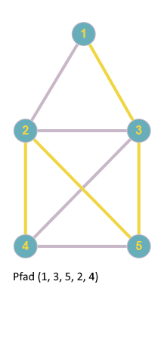
Sei $G=(V,E)$ ein Graph. Ein Teilgraph $G' \text{ von } G$ ist ein Graph $(V',E')$ mit $V' \subset V(G)$ und $E' \subset E(G).$ Wenn der Teilgraph $G'$ zwischen seinen Knoten die gleichen Kanten hat wie $G$ (also $\forall v,w \in V(G'): \{v,w\} \in E(G') \Leftrightarrow \{v,w\} \in E(G)$), dann nennt man $G'$ induzierten Teilgraph oder auch Untergraph. (Entsprechende Definition für gerichtete und Multigraphen). Also muss man für einen (induzierten) Untergraphen nur seine Knotenmenge angeben.
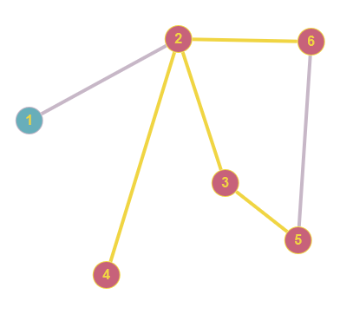
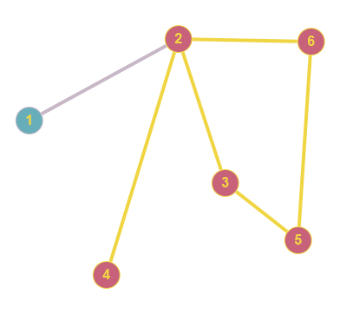
Obige Abbildung zeigt links einen Teilgraphen (rote Knoten, gelbe Kanten), rechts einen Untergraphen.
Definition 1.11
Sei $p \in \mathbb{N}$ mit $p \leq n(G)$. Dann heißt ein Untergraph $C$ von $G$ mit $C \cong K_p$ eine p-Clique in $G$. $C$ ist ein induzierter Untergraph.
Um den Begriff des Zusammenhanges definieren zu können benötigt man den Begriff des Weges.
Definition 1.12 (Weg)
Sei $G = (V,E)$ Graph (egal ob gerichtet oder nicht, egal ob Mehrfachkanten vorkommen) und $W=(v_1, \cdots, v_n)$ ein n-Tupel von Knoten aus $V$, sodass für alle $i \in \{1, \cdots, n-1\}$ gilt:
- $\{v_i, v_{i+1}\} \in E$, falls $G$ ungerichteter Graph ohne Mehrfachkanten ist
- $(v_i, v_{i+1}) \in E$, falls $G$ gerichteter Graph ohne Mehrfachkanten ist
- $E(\{v_i, v_{i+1}\}) > 0$, falls $G$ ungerichteter Graph mit Mehrfachkanten ist
- $E((v_i, v_{i+1})) > 0$, falls $G$ ungerichteter Graph mit Mehrfachkanten ist.
$v_i$ und $v_{i+1}$ sind also jeweils durch eine Kante verbunden. $W$ nennt man ungerichteten Weg, wenn $G$ ungerichtet ist, gerichteten Weg, wenn $G$ gerichtet ist. $v_1$ heißt Startknoten, $v_n$ Endknoten des Weges. Als Weglänge bezeichnen wir die Anzahl der Kanten des Weges.
In Definition 2.1 wird dieser Begriff wiederholt und spezielle Wege eingeführt.
Definition 1.13 (Zusammenhang)
Ein ungerichteter Graph $G$ heißt zusammenhängend, wenn es zwischen je zwei beliebigen Knoten aus $V$ einen ungerichteten Weg in $G$ gibt, der sie verbindet.
Ein gerichteter Graph $G$ heißt stark zusammenhängend, wenn für je zwei beliebige Knoten $u$ und $v$ aus $V$ sowohl einen gerichteten Weg von $u$ nach $v$ gibt, als auch umgekehrt.
Ein gerichteter Graph $G$ heißt schwach zusammenhängend, wenn der zugehörige ungerichtete Graph zusammenhängend ist.
Eine Zusammenhangskomponente $U$ eines Graphen $G$ ist ein maximal zusammenhängender Untergraph, d.h. es gilt:
1.) Der Untergraph $U$ ist zusammenhängend
2.) Für jeden Knoten $v \in G \setminus U$ ist der Untergraph $U \cup \{v\}$ nicht zusammenhängend.
Bemerkung
Man kann die Eigenschaft, dass zwei beliebige Knoten durch einen Weg in $G$ verbunden sind, als Äquivalenzrelation auf V auffassen. Die daraus entstehenden Äquivalenzklassen ergeben die Zusammenhangskomponeneten, wenn man von den Äquivalenzklassen zu den durch sie induzierten Teilgraphen (=Untergraphen) von $G$ übergeht. [44]
1.1 Adjazenz, Inzidenz, Laplace und Grad
Definition 1.14 (Adjazenzmatrix) [14]
Sei $G=(V,E)$ ein Graph, $n=n(G), V=\mathbb{N}_n, A=(a_{i,j}), \; i, j \in \mathbb{N}_n.$ Die Festlegung der Knotennamen auf die ersten $n$ natürlichen Zahlen ist im Sinne der Isometrie durch Umbenennung immer möglich.
Dann nennen wir $A \in \mathbb{R}^{n\times n}$ Adjazenzmatrix (auch $A(G)$), wenn in
a) Graphen ohne Kantengewichte, ohne Mehrfachkanten
$$a_{i,j}=\begin{cases}
1 \text{ falls } (i,j) \in E \text{ bzw. } \{i,j\} \in E \\
0 \text{ sonst}
\end{cases}
$$


b) Graphen ohne Kantengewichte, mit Mehrfachkanten
$$
a_ {i,j}=E((i,j)) \text{ falls } (i,j) \in E \text{ bzw. } E(\{i,j\}) \text{ falls }\{i,j\} \in E \\
$$


c) Graphen mit Kantengewichten (Kantengewichtsfunktion $g$), ohne Mehrfachkanten
$$a_{i,j}=\begin{cases}
g((i,j)) \text{ falls } (i,j) \in E \text{ bzw. } g(\{i,j\}) \text{ falls } \{i,j\} \in E \\
0 \text{ sonst}
\end{cases}
$$


Für Graphen mit Kantengewichten und Mehrfachkanten definiert man keine Adjazenzmatrix.
In einer Adjazenzmatrix ist ablesbar, welche Knoten durch eine Kante verbunden sind (bze. durch wieviele Kanten zwei Knoten verbunden sind und bei c) mit welchem Gewicht sie das tut.
in den Fälle a) und b) kann man die Adjazenzmatrix als Darstellung der Funktion $\mathfrak{E}$ aus Definition 1.1' betrachten.
Aus einer Adjazenzmatrix kann man das Aussehen des Graphen qualitativ rekonstuieren, will heißen, dass man einen isomorphen Graphen erhält. Folgender Satz stellt einige grundlegende Eigenschaften von Adjazenzmatrizen zusammen.
Für die Definition eines Weges und eines Pfades siehe Definition 1.12 bzw. 2.1.
Satz 1.15
a) $G$ ungerichtet $\Leftrightarrow A$ symmetrisch
b) $G$ schleifenfrei $\Leftrightarrow a_{i,i}=0$ für alle $i=1\cdots n$
c) $G$ ungerichtet: $G$ zusammenhängend $\Leftrightarrow A$ irreduzibel
d) $G$ gerichtet: $G$ stark zusammenhängend $\Leftrightarrow A$ irreduzibel
e) $G$ gerichtet: $A^T + A $ irreduzibel $\Rightarrow G$ schwach zusammenhängend. Dann ist $A^T + A$ die Adjazenzmatrix des $G$ zugrundeliegenden ungerichteten Graphen
f) Sind zwei Adjazenzmatrizen gleich, dann sind daraus zu konstruierende Graphen isomorph.
g) Die Adjazenzmatrix des vollständigen Graphen hat auf der Hauptdiagonale Nullen und sonst überall Einsen.
h) $G$ habe keine Kantengewichte, aber Mehrfachkanten sind zugelassen (Fall b). Dann ist $A(i,j):=a_{i,j}$ die Anzahl der Wege der Länge 1 von $i$ nach $j$. Allgemein ist $A^k(i,j)$ die Anzahl der Wege der Länge k von i nach j.
i) Wenn in g) keine Mehrfachkanten erlaubt sind, dann gilt die gleiche Aussage für Pfade statt Wege
j) Sei $B = (b_{i,j}) = \sum_{i=0}^k A^i \quad (A^0=I)$ und $R_k$ definiert durch $r_{i,j}=\begin{cases} 1 \text{ für } b_{i,j} > 0 \\ 0 \text{ für } b_{i,j} = 0 \end{cases}$
Dann ist $R_k$ die Matrix, die angibt, ob ein Knoten j vom Knoten i aus in maximal k Schritten erreichbar ist, nämlich dann, wenn $r_{i,j} = 1$ ist. Wenn $R_k = R_{k+1}$, dann nennt man $R := R_n$ Erreichbarkeitsmatrix.
Ausflug in die Lineare Algebra
Der in Satz 1.15 benutzte Begriff "irreduzibel" stammt aus der linearen Algebra. Er besagt einfach ausgedrückt, dass die Matrix nicht durch Vertauschen von Zeilen und Spalten so umgeordnet werden kann, dass eine untere Blocksdreiecksgestalt entsteht. Zunächst die exakte Definition.
Definition 1.16 (reduzibel)
Eine Matrix $A \in \mathbb{R}^{n \times n}$ heißt reduzibel, wenn es eine Permutationsmatrix $P$ gibt, so dass
$$
PAP^T = \left(
\begin{array}{cc}
A_{MM} & 0 \\
A_{NM} & A_{NN}\\
\end{array}
\right)
$$
$A_{MM}$ ist eine Blockmatrix aus $\mathbb{R}^{p\times p}, p \in \{1, 2, \cdots , n-1\}$. Die anderen beiden Matrizen sind passend dimensioniert anzunehmen. Sonst heißt die Matrix irreduzibel.
Man beachte, das die Blockmatrizen $A_{MM}$ und $A_{NN}$ quadratisch sind; die 0 steht für eine rechteckige Blockmatrix, die nur Nullen enthält. Wenn z.B. $n=7$ ist und M=5, dann muss N=2 sein und die Blockmatrix mit den Nullen hat dann 5 Zeilen und 2 Spalten.
Eine Permutationsmatrix $P$ hat in jeder Zeile und jeder Spalte genau eine 1, sonst Nullen. Etwas formaler gesagt:
Definition 1.17 (Permutationsmatrix)
Sei $\pi$ eine Permutation der ersten n natürliche Zahlen. Dann ist eine Permutationsmatrix $P_\pi \in \mathbb{R}^{n \times n}$ definiert als
$P_\pi=(p_{i,j})$ mit $p_{i,j} = \delta_{\pi(i),j}$
Bemerkung
Permutationsmatrizen entstehen aus der Einheitsmatrix durch Zeilen- (oder Spalten-) Vertauschungen; eins von beidem reicht.
Eigenschaften:
Satz 1.17a
a) Eine Permutationsmatrix ist regulär und orthogonal; $P_\pi^{-1} = P_\pi^T=P_{\pi^-1}$
b) $P_{\pi \circ \sigma} = P_{\sigma} \cdot P_{\pi}$
c) Die Potenz einer Permutationsmatrix ist wieder eine Permutationsmatrix. Es gibt ein $k \in \mathbb{N}: \; P_\pi^k = I$.
d) $\det{P_\pi} = \text{sgn}(\pi)$
e) Die Eigenwerte einer Permutationsmatrix liegen auf dem komplexen Einheitskreis.
Beispiel:
$$
\pi =(1,2) \quad
P_\pi=\left(
\begin{array}{ccc}
0 & 1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1 \\
\end{array}
\right)
\quad
A=\left(
\begin{array}{ccc}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9 \\
\end{array}
\right)
\quad
P_\pi^T=P_\pi
\quad
P_\pi \cdot A \cdot P_\pi^T =
\left(
\begin{array}{ccc}
5 & 4 & 6 \\
2 & 1 & 3 \\
8 & 7 & 9 \\
\end{array}
\right)
$$
In diesem Beispiel werden die Zeilen 1 und 2 und die Spalten 1 und 2 vertauscht, wobei es hier egal ist, in welcher Reihenfolge das passiert.
Nun noch ein paar Eigenschaften irreduzibler Matrizen.
Satz 1.18
a) Mit $A$ ist auch $A^T$ irreduzibel.
b) Sei $A \in \mathbb{R}^{n \times n} \geq 0$ und es existiere ein $k \in \mathbb{N}: A^k > 0$. Dann ist A irreduzibel.
c) Sei $A \in \mathbb{R}^{n \times n} \geq 0$. $A$ irreduzibel $\Leftrightarrow \forall i,j \in \mathbb{N}_n \; \exists k \in \mathbb{N}: A^k(i,j) > 0$.
Da im Weiteren auch Eigenwerte von Matrizen eine Rolle spielen, hier kurz eine Zusammenstellung der dort gebrauchten Eigenschaften:
Satz 1.18b
a) Die Summe der Eigenwerte ist gleich der Spur der Matrix. Unter Spur versteht man die Summe der Hauptdiagonalelemente.
b) Eigenwert von $A^k$ = $\text{(Eigenwert von } A )^k$.
Soweit der Ausflug in die lineare Algebra.
Als Erstes ein Satz über die Isomorphie von Graphen:
Satz 1.18a [35] [41]
Seien $G_1$ und $G_2$ zwei Graphen mit derselben Knotenmenge. Die beiden Graphen sind genau dann isomorph, wenn es eine Permutationsmatrix $P$ gibt, sodass $P^T A(G_1) P = A(G_2)$. Somit haben isomorphe Graphen ähnliche Adjazenzmatrizen (da die Permutationsmatrizen regulär sind). Also haben isomorphe Graphen das gleiche charakteristische Polynom und die gleichen Eigenwerte.
Damit können wir von dem charakteristischen Polynom und den Eigenwerten eines Graphen reden.
Und nun zu einem konkreten Beispiel für einen nicht zusammenhängenden Graphen und seine Adjazenzmatrix. Der folgende ungerichtete Graph ist nicht zusammenhängend, dementsprechend muss seine Adjazenzmatrix reduzibel sein.
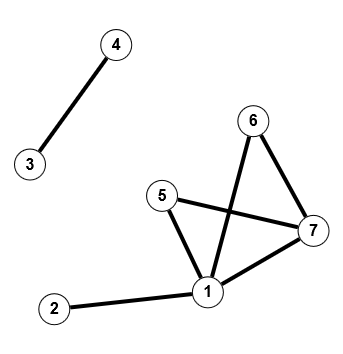

Man sieht, dass durch Vertauschen der ersten und dritten und der zweiten und vierten Zeile eine untere Blockdreiecksmatrix entsteht. Das gleichzeitige Tauschen der zugehörigen Spalten ändert in diesem Fall daran nichts, muss aber gemacht werden, da ja $P\cdot A \cdot P^T$ gefordert ist; also:
$$
P=\left(
\begin{array}{ccccccc}
0&0&1&0&0&0&0\\
0&0&0&1&0&0&0\\
1&0&0&0&0&0&0\\
0&1&0&0&0&0&0\\
0&0&0&0&1&0&0\\
0&0&0&0&0&1&0\\
0&0&0&0&0&0&1\\
\end{array}
\right),
\quad
P^T=P,
\quad
P \cdot A \cdot P^T =
\left(
\begin{array}{ccccccc}
0&1&0&0&0&0&0\\
1&0&0&0&0&0&0\\
0&0&0&1&1&1&1\\
0&0&1&0&0&0&0\\
0&0&1&0&0&0&1\\
0&0&1&0&0&0&1\\
0&0&1&0&1&1&0\\
\end{array}
\right)
\quad
A_{2,2}=
\left(
\begin{array}{cc}
0&1\\
1&0\\
\end{array}
\right)
\quad
A_{5,5}=\left(
\begin{array}{ccccc}
0&1&1&1&1\\
1&0&0&0&0\\
1&0&0&0&1\\
1&0&0&0&1\\
1&0&1&1&0\\
\end{array}
\right)
\quad
A_{5,2}=
\left(
\begin{array}{cc}
0&0\\
0&0\\
0&0\\
0&0\\
0&0\\
\end{array}
\right)
$$
Verbindet man andererseits die beiden Zusammenhangskomponenten des obigen Graphens kann man mit Hilfe von Satz 1.18 die Irreduzibilität zeigen:
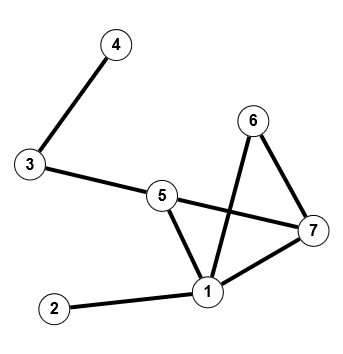

Durch Multiplikation der Adjazenzmatrix mit sich selbst erhält man bei $A^6$ eine Matrix mit lauter positiven Elementen, damit ist der Graph zusammenhängend. Ihre tatsächlichen Werte sind ohne Belang und werden hier nicht wiedergegeben.
Da einem Graphen eine Matrix zugeordnet ist, kann man sich fragen, welche anderen Eigenschaften von Matrizen auch für Graphen interessant sind bzw. auf Graphen übertragen werden können. Die Spektrale Graphentheorie [15] befasst sich mit dieser Frage, indem sie Aussagen über die Eigenwerte von Adjazenzmatrizen macht.
Definition 1.19 (Charakteristisches Polynom, Eigenwerte)
Sei $G$ ein ungerichteter Graph. $A_G$ sei die zugehörige Adjazenzmatrix. Dann wird das charakteristische Polynom $P_G(x) = \det(A_G - x \cdot I)$ von $A_G$ auch charakteristisches Polynom von $G$ genannt; ebenso werden die Eigenwerte von $A_G$ Eigenwerte des Graphen genannt. Die Menge der Eigenwerte bildet das Spektrum des Graphen.
Satz 1.20
a) Ein ungerichteter Graph $G$ hat nur reelle Eigenwerte.
b) Der vollständige Graph $K_n$ hat das Spektrum $\lambda_1 = n-1, \; \lambda_2 = \cdots = \lambda_n = -1$.
c) Der vollständige bipartite Graph (siehe Definition 3.3) $K_{r,s}$ hat das Spektrum $\lambda_1 = \sqrt{r\cdot s}, \; \lambda_2 = \lambda_3 = \cdots = \lambda_{r+s-1} = 0, \; \lambda_{r+s}=-\sqrt{r \cdot s}$.
d) $G$ habe die Zusammenhangskomponenten $G_1, \cdots , G_r$. Dann gilt für das charakteristische Polynom
$P_G(x) = P_{G_1}(x) \cdot P_{G_2}(x) \cdots P_{G_r}(x)$. Somit bestimmt das Spektrum der Zusammenhangskomponenten das Spektrum des gesamten Graphens.
e) Bei einem schleifenfreien Graphen ist die Summe der Eigenwerte gleich Null. (Siehe Satz 1.18b a)
f) Für jeden Eigenwert $\lambda$ von $G$ gilt $|\lambda| \leq \Delta(G)$ (Maximalgrad).
g) $G$ hat genau dann den Eigenwert $\Delta(G)$, wenn $G$ regulär ist.
h) Ist $-\Delta(G)$ ein Eigenwert von $G$, dann ist $G$ regulär und bipartit.
i) Ein bipartiter Graph $G$ hat mit einem Eigenwert $\lambda$ stets auch $-\lambda$ als Eigenwert von $G$.
j) Haben zwei Graphen unterschiedliche Eigenwerte, sind sie nicht isomorph.
k) Bei einem ungerichteten Graphen $G$ gilt für seine Adjazenzmatrix $A$:
(1) Spur($A$) = 0
(2) Spur($A^2$) = 2 m(G) (= 2 mal die Anzahl der Kanten)
(3) Spur($A^3$) = 6 $\cdot$ Anzahl der Dreiecke von $G$.
Der Zusammenhang zu den Eigenwerten besteht in Punkt e). Darüber hinaus folgt, dass das Spektrum die Anzahl der Kanten, Knoten und Dreiecke festlegt. (Siehe Satz 1.18b b))
Leider bestimmt das Spektrum eines Graphen nicht eindeutig seine Struktur (im Sinne der Isomorphie, Satz 1.20j ist keine Äquivalenz). Dies sei an einem Beispiel kurz gezeigt.
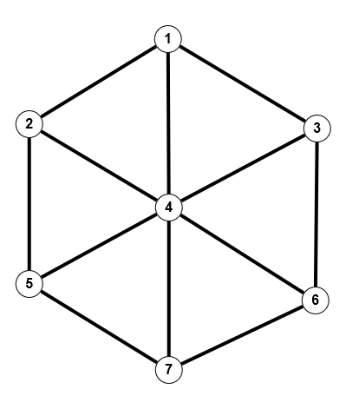

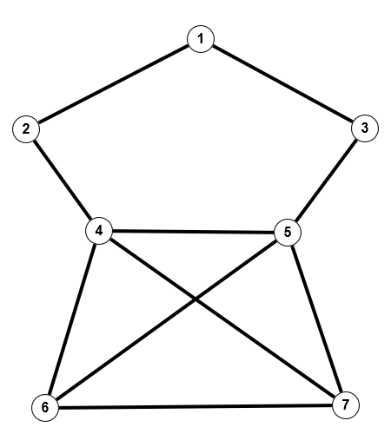

Dass die beiden Graphen nicht isomorph sind sieht man leicht am Knoten 4 des linken Graphen, der den Grad 6 hat; einen Knoten mit diesem Grad gibt es beim rechten Graphen nicht. Beide Graphen haben das gleiche Charakteristische Polynom $p(\lambda) = (\lambda + 2)(\lambda^2 - 2\lambda - 6)(\lambda - 1)^2(\lambda + 1)^2$ und damit auch die gleichen Eigenwerte $\{-2, 1 \pm \sqrt(7), 1,1,-1,-1\}$.
Aber was kann man mit dieser Spektraltheorie denn nun anfangen? Ich habe den Hinweis gefunden, dass es für das automatisierte Zeichnen von Graphen ein Verfahren gibt, das sog. Spektral-Layout, das Eigenwerte und Eigenvektoren der Adjazenzmatrix (oder auch der später eingeführten Laplace-Matrix) benutzt, um Graphen ausgehend von der Adjazenzmatrix zu zeichnen. Ja, es ist tatsächlich keine uninteressante Fragestellung, wie man aus der Adjazenzmatrix, die ja bis auf Isomorphie das Aussehen des Graphen bestimmt, automatisiert eine Zeichnung des Graphen erstellen kann. Hier wird in [15] ein Algorithmus von Hall [16] genannt; eine andere Lösung findet sich in [17].
Ich werde auf dieses Verfahren in einem eigenen Kapitel eingehen und setze hier zunächst die Vorstellung weiterer Darstellungsmatrizen für Graphen fort.
Die Inzidenzmatrix sagt etwas über das Zusammentreffen von Knoten und Kanten aus.
Definition 1.21 (Inzidenzmatrix) [18]
Sei $G=(V,E)$ kein Multigraph, $\quad n=n(G),\; m=m(G)$. Eine Matrix $B=(b_{i,j}) \in \mathbb{R}^{n \times m}$ heißt Inzidenzmatrix, wenn
a) für schleifenfreie ungerichtete Graphen $ b_{i,j} = \begin{cases} 1 \text{ falls } v_i \in e_j \\ 0 \text{ sonst} \end{cases}$
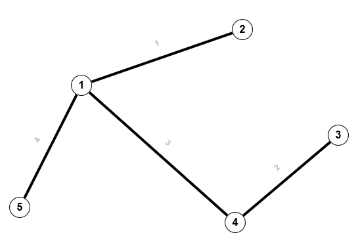
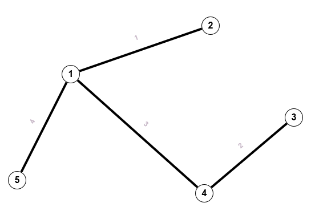
 Die Inzidenzmatrix ist 5x4.
Die Inzidenzmatrix ist 5x4.b) für schleifenfreie gerichtete Graphen $b_{i,j} = \begin{cases} 1 \text{ falls } \exists x \in V:e_j =(v_i,x) \\ 0 \text{ falls } v_i \notin e_j \\
-1 \text{ falls } \exists x \in V:e_j =(x,v_i) \end{cases}$ mit beliebigem Knoten x.
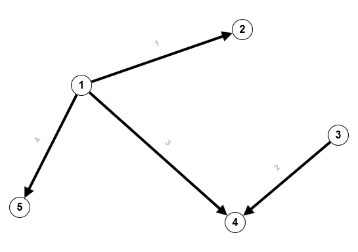
 Die Inzidenzmatrix ist 5x4.
Die Inzidenzmatrix ist 5x4.Beobachtung 1.22
a) In einer Inzidenzmatrix eines ungerichteten Graphen enthält jede Spalte genau 2 von Null verschiedene Einträge, deren Summe 2 ergibt.
b) In einer Inzidenzmatrix eines gerichteten Graphen enthält jede Spalte genau 2 von Null verschiedene Einträge, deren Summe 0 ergibt.
Definition 1.23 (Gradmatrix)
Sei $G=(V,E), \quad n=n(G)$. Eine Diagonalmatrix $D=(d_{i,i}) \in \mathbb{R}^{n \times n}$ heißt Gradmatrix, wenn $d_{i,i} = d_G(v_i)$.
Zu dem Graphen unter Definition 1.21 gehört folgende Gradmatrix:

Satz 1.24
Sei $G$ ein ungerichteter Graph, B seine Inzidenzmatrix, A seine Adjazenzmatrix und D seine Gradmatrix. Dann gilt:
$$
A + D = B \cdot B^T
$$
Als letztes betrachten wir nun noch die Laplace-Matrix, die in gewisser Weise die Gradmatrix und die Adjazenzmatrix vereinigt.
Definition 1.25 (Laplacematrix) [19]
Sei $G=(V,E) \text{ einfacher Graph, } n=n(G)$. Eine Matrix $L=(l_{i,j}) \in \mathbb{R}^{n \times n}$ heißt Laplace-Matrix, wenn
$ l_{i,j} = \begin{cases} d_G(v_i) \text{ falls } i = j \\ -1 \text{ falls } i \neq j \text{ und } v_i \text{ benachbart zu } v_j \\ 0 \text{ sonst} \end{cases}.$


Satz 1.26
Sei $G$ einfacher Graph mit Adjazenzmatrix $A$, Gradmatrix $D$ und Inzidenzmatrix $B$. Dann gilt:
a) $L = D - A$
b) Wenn $G$ d-regulär ist, dann gilt speziell $L = d \cdot I - A$
c) $L = B^T\cdot B$
d) $L$ ist symmetrisch, damit sind alle Eigenwerte reell
e) $L$ ist positiv-semidefinit (was bedeutet, dass alle Eigenwerte von $L$ nichtnegativ sind)
f) Die Spalten- und die Zeilensummen von $L$ sind Null.
g) Der kleinste Eigenwert von $L$ ist 0, der zugehörige Eigenvektor ist $\alpha \cdot 1_n, \; 1_n:=(1,1,1, \cdots, 1)^T$
h) Die algebraische Vielfachheit dieses Eigenwertes 0 ist die Anzahl der Zusammenhangskomponenten von $G$.
1.2 Spektral Layout
Der hier gezeigte Algorithmus basiert auf den Eigenvektoren der Adjazenzmatriz bzw. Laplace-Matrix; er wird von Y. Koren in [17] vorgestellt. Ich habe ihn, abgesehen von der relativ einfachen Realisierung, vor allem deshalb ausgesucht, weil er ohne zusätzlichen Aufwand auch dreidimensionale Graphen erstellen kann.
Die Grundidee besteht darin, bestimmte Eigenvektoren der Adjazenz- oder Laplace-Matrix als Koordinaten für das Zeichnen der Knoten zu verwenden. Genauer, man nimmt für eine 2-D-Zeichnung die beiden Eigenvektoren der Laplace-Matrix, die zu den beiden kleinsten Eigenwerten ungleich Null gehören (siehe Satz 1.25g) und verwendet die i-ten Komponenten als Koordinaten $(x_i, y_i)$ für den Knoten i. Für eine dreidimensionale Darstellung nimmt man einfach den nächsten Eigenvektor dazu. Dabei müssen die Eigenvektoren orthonormalisiert werden.
Entwickelt man mit diesen Angaben drauf los, stößt man schnell an Grenzen, einfach weil allein die Berechnung der Eigenvektoren einer großen Matrix sehr aufwändig ist ebenso wie ihre Orthonormalisierung, vor allem wenn man bedenkt, dass man nur 2 oder 3 davon benötigt.
Statt dessen berechnet der Algorithmus von Koren nur p-viele orthonormalisierte Eigenvektoren $u^2, \cdots, u^p$, wobei p sinnvollerweise 2 oder 3 ist. Ausgangspunkt ist hier die Matrix $D^{-1}A$, wobei D die Gradmatrix und A die Adjazenzmatrix ist. Von der zugehörigen Laplace-Matrix wissen wir (Satz 1.25g), dass $1_n$ Eigenvektor zum Eigenwert 0 ist. Es folgt:
$$
D^{-1}\cdot A \cdot 1_n \underset{1.25a}{=} D^{-1}(D - L) 1_n=(I-D^{-1}L)1_n = 1_n - D^{-1}L1_n = 1_n
$$
Also ist $1_n$ Eigenvektor von $D^{-1}A$ zum Eigenwert 1. Der Koren-Algorithmus berechnet nun nacheinander weitere Eigenvektoren $u^2, u^3, \cdots, u^p$ und sorgt dafür (Gram-Schmidt-Orthogonalisierung), dass die $u^k$ aufeinander senkrecht (im Sinne des Inneren Produktes $<u,Dv>$) stehen und auf 1 normiert sind. Die weiteren Eigenvektoren werden iterativ durch fortlaufende Multiplikation mit $\frac{1}{2}(I+D^{-1}A)$ erzeugt, was überdies bewirkt, dass sich die Eigenwerte im Intervall $[0,1]$ tummeln. Gestartet werden die Iterationen für jeden weiteren zu berechnenden Eigenvektor mit einem zufällig erzeugten Startvektor. Dieses "Power-Iteration" genannte Verfahren ist laut Koren konvergent.
Für jeden zu berechnenden Eigenvektor $u^k$:
Erzeuge zufällligen Startvektor
Normiere Startvektor
Wiederhole
D-Orthogonalisiere Startvektor mit allen anderen schon vorhandenen Eigenvektoren, erhalte $u^k$
Multipliziere den Ergebnisvektor $u^k$ mit $\frac{1}{2}(I+D^{-1}A)$, erhalte $\tilde{u}^k$
Normiere diesen Vektor $\tilde{u}^k$
bis $\tilde{u}^k$ parallel zu $u^k$.
Speichere $\tilde{u}^k$ als neuen Eigenvektor ab.
Ich habe den exakten Algorithmus in Maple programmiert, da Maple eine sehr leistungsfähige graphische Unterstützung bietet.
Als erste Adjazenzmatrix habe ich die des Graphen über Definition 1.19 verwendet.
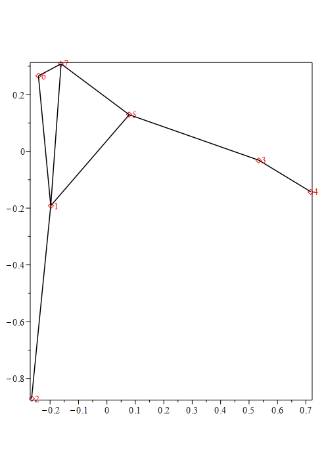
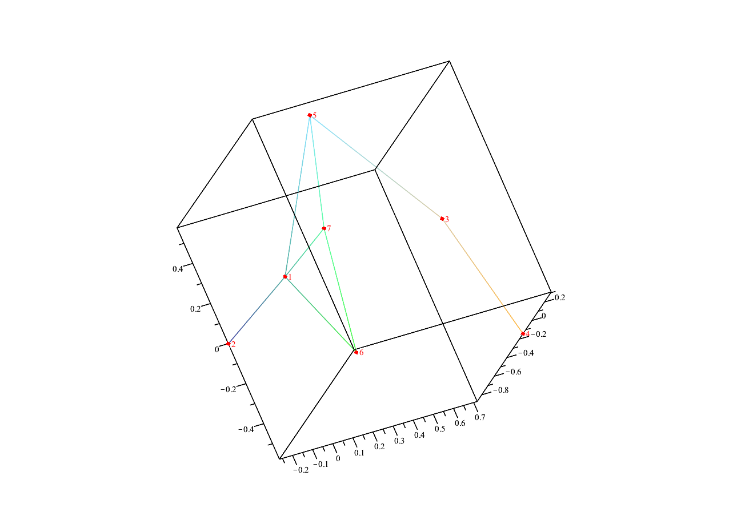
Die zweite Matrix ist durch Vervierfachung der ersten entstanden: $7 \times 7 \rightarrow 14 \times 14$. Dadurch erklärt sich die Ähnlichkeit der beiden zweidimensionalen Graphen.
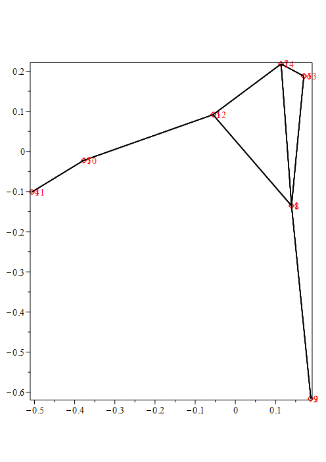
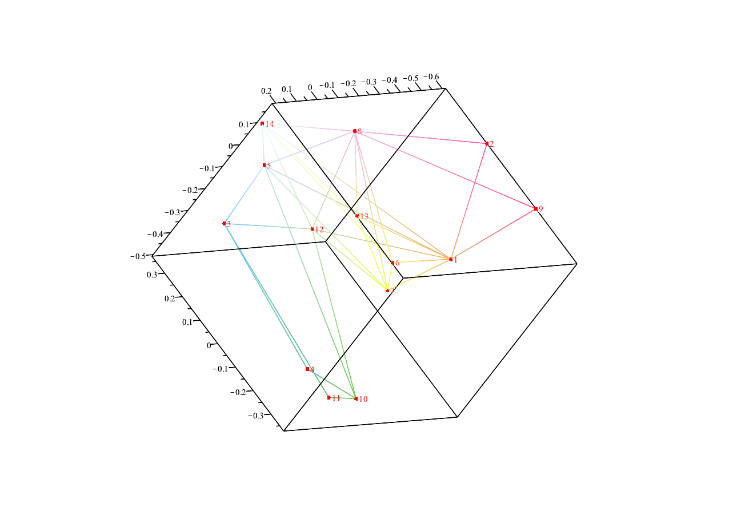
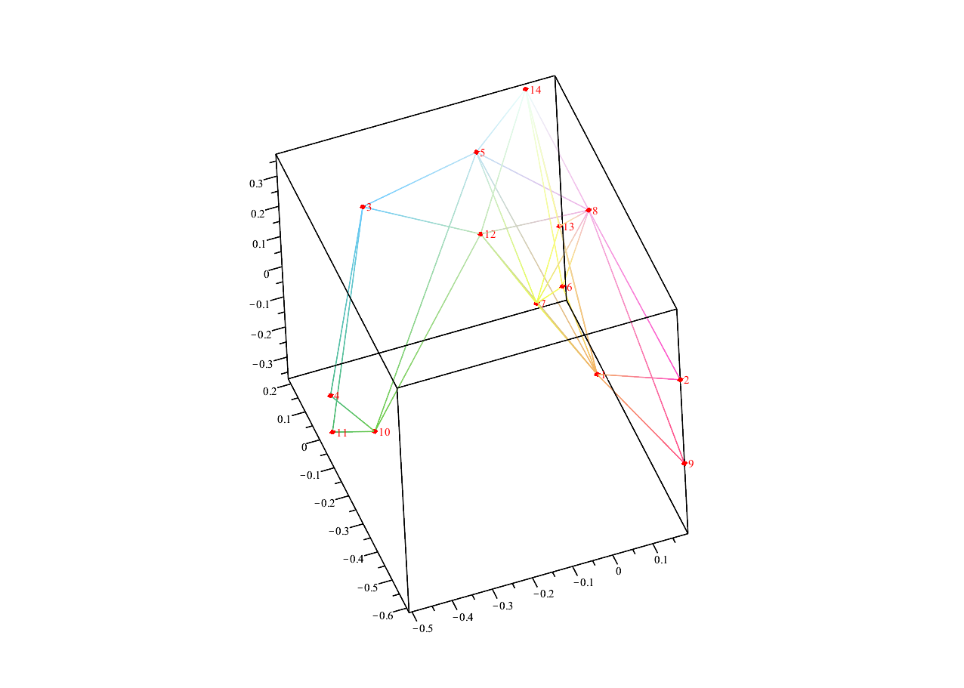
Als drittes Beispiel habe ich einen Graph mit 30 Knoten zeichnen lassen. Die Beispiele im Aufsatz von Koren zeigen mehrerer 100 Knoten.

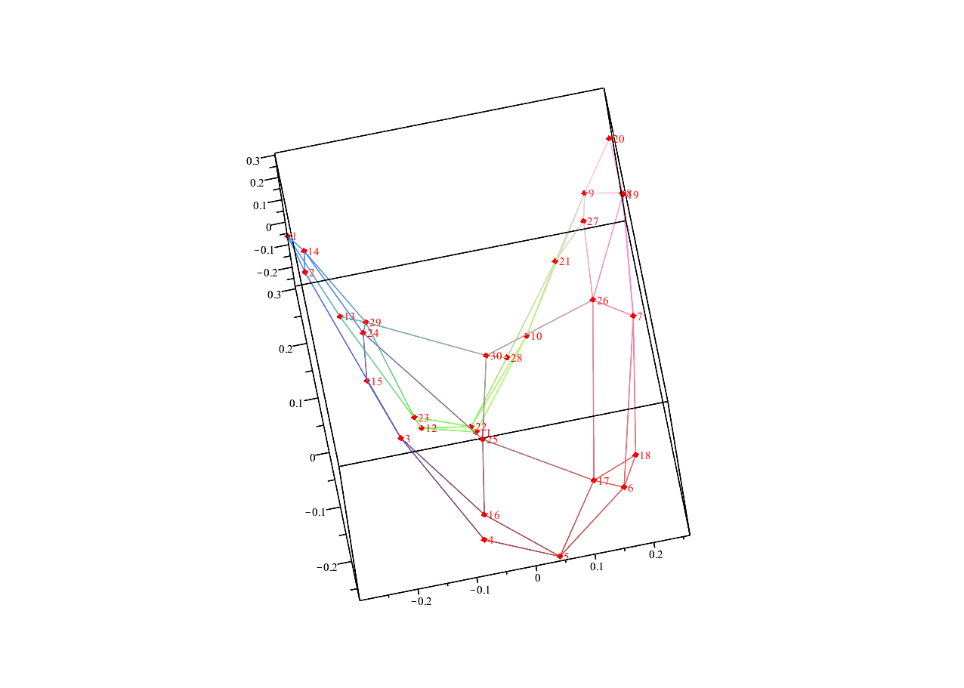
Das Aussehen der Graphen hängt im Übrigen von dem zufälligen Startvektor ab.
1.3 Der Zufallswanderer
Fragestellung: Wie groß ist die Wahrscheinlichkeit, dass der Wanderer zuerst an dem Ausgangsknoten vorbeikommt, bevor er den Knoten mit der Falle erreicht?
Schauen wir uns mal ein Beispiel an:
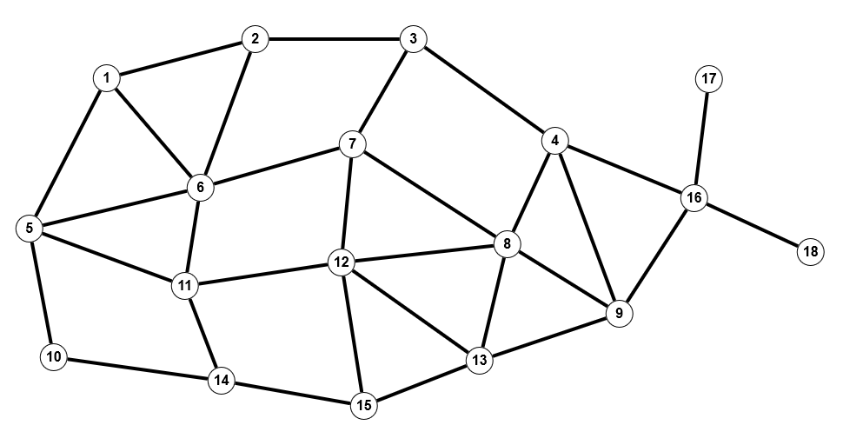
Nehmen wir weiter an, dass der Knoten 10 der Ausgang ist, der Knoten 12 die Falle und der Knoten 2 der Startknoten des Wanderers. Bezeichne $x(i) \in V$ den Aufenthaltsort des Wanderers im i-ten Schritt, also $x(0) = v_2$. Und um wahrscheinlichkeitstheoretisch korrekt argumentieren zu können, nennen wir Z das Ereignis, dass der Wanderer zuerst in $v_a$ und dann erst in $v_f$ ankommt (was er natürlich nicht mehr tut, wenn er den Ausgang gefunden hat). Klar ist, dass zwei Wahrscheinlichkeiten von vorne herein feststehen, nämlich die Fälle $v_w=v_a$ oder $v_w=v_f$. Es gilt:
$$P(Z|x(0) = v_a) = 1$$
$$P(Z|x(0) = v_f) = 0$$
Wir suchen nun die Wahrscheinlichkeit $p_w = P(Z|x(0)=v_w)$, gemäß oben angenommenen Beispiel also $p_2=P(Z|x(0)=v_2)$.
Mit Hilfe der Wahrscheinlichkeitsrechung formen wir um:
$$p_2=P(Z|x(0)=v_2)=P(Z \wedge x(1) = v_1) \vee P(Z \wedge x(1) = v_3) \vee P(Z \wedge x(1) = v_6)$$
Sind zwei Wahrscheinlichsereignisse mit "oder" verbunden, dann addieren sich die Wahrscheinlichkeitswerte:
$$p_2=P(Z|x(0)=v_2)=P(Z \wedge x(1) = v_1) + P(Z \wedge x(1) = v_3) + P(Z \wedge x(1) = v_6)$$
Ebenso lässt sich unter Verwendung bedingter Wahrscheinlichkeiten weiter umformen:
$$p_2=P(Z|x(1)=v_1) \cdot P(x(1)=v_1) + P(Z|x(1)=v_3) \cdot P(x(1)=v_3) + P(Z|x(1)=v_6) \cdot P(x(1)=v_6) =$$
$$\frac{1}{3}p_1 + \frac{1}{3}p_3 + \frac{1}{3}p_6 = \frac{1}{3}(p_1 + p_3 +p_6)$$
Es zeigt sich, dass sich die Startwahrscheinlichkeit $p_2$ aus den Startwahrscheinlichkeiten an den benachbarten Konten und der Wahrscheinlichkeit mit der eine Kante ausgewählt wird zusammensetzt. Dies lässt sich leicht verallgemeinern (es bezeichne $N_i$ die Knotennummern der zu $v_i$ benachbarten Knoten):
$$ p_i=P(Z|x(0)=v_i)=\sum_{j \in N_i} P(Z \wedge x(1) = v_j)=\frac{1}{d_G(v_i)}\sum_{j \in N_i} p_j \quad (*) $$
Diese Gleichungen gelten für alle $i \in \{1, \cdots, n(G)\} \setminus \{a,f\}$.
Zunächst kann man diese Gleichungen etwas kompakter schreiben. Zu diesem Zweck definiere ich eine Matrix A, die Adjazenzmatrix.
Die Adjazenzmatrix zu obigem Graphen hat folgendes Aussehen, wobei die Kommata zur besseren Lesbarkeit eingefügt wurden:
0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0
1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0
1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0
0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0
0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0
A = 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0
0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0
0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0
0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0
0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0
0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0
0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0
Netterweise kann man das Gleichungssystem (*) mit Hilfe dieser Matrix schreiben, denn die $p_i$ kommen mit dem Faktor 1 oder 0 vor und entsprechen genau dem Nachbarschaftsverhältnis. Dabei ignorieren wir zunächst die Tatsache, dass es einen Ausgangsknoten und einen Fallenknoten gibt. Dazu bringen wir die Knotengrade auf die linke Seite und fassen Sie zu einer Diagonalmatrix $D$ zusammen: $d_{i,i}=grad(v_i)$. Schließlich bezeichne $p:=(p_1, p_2, p_3, ..., p_{N(G)})$ den aus den Wahrscheinlichkeiten zusammengesetzten Vektor und wir erhalten:
$$ D\cdot p = A \cdot p$$
Und wenn man will, geht das noch etwas kompakter mit der Laplace-Matrix $L:= D - A$ als $L \cdot p = 0$. Dies sieht wie ein homogenes lineares Gleichungssystem aus, ist es aber nicht, wenn man sich in Erinnerung ruft, dass zwei Werte von $p$ ja festliegen. Um die unbekannten Werte von $p$ zu berechnen, formt man weiter um. Als rechte Seite eines inhomogenen Gleichungssystems $r$ wählt man die negative Spalte mit der Nummer $a$ der Matrix $L$, wobei man die Werte mit dem Index $a$ und $f$ weg lässt. Somit ist $r$ ein Vektor der Dimension $n(G) -2$. Ist ja klar, denn wir wollen ja auch nur $n(G)-2$ Werte von $p$ berechnen. Wenn man jetzt noch die Matrix $C$ durch Weglassen der Zeilen und der Spalten mit den Nummern $a$ und $f$ aus der Matrix $L$ erzeugt, ist das zu lösende Gleichungssystem
$$C\cdot \tilde{p} = r$$.
Dieses Gleichungssystems ist lösbar, da $C$ maximalen Rang hat (also regulär ist). Der Lösungsvektor $\tilde{p}$ enthält alle Wahrscheinlichkeiten für Startpunkte ungleich $v_a$ und $v_f$; durch Einfügen von 1 und 0 an den besagten Stellen ergibt sich:
.400851169457537
.322543492572121
.21295683528478
.146873382142279
.526187542826443
.353822472974046
.16945363113994
.111035216300932
p = .126709857274843
1.0
.35007652887419
0.
.1121392109476
.520296099696271
.210811770214624
.136791619708561
.136791619708561
.136791619708561
Somit $v_5$ der "beste" Startpunkt, also mit der höchsten Wahrscheinlichkeit den Ausgang vor der Falle zu finden, direkt gefolgt von $v_{14}$, was nicht wundert.
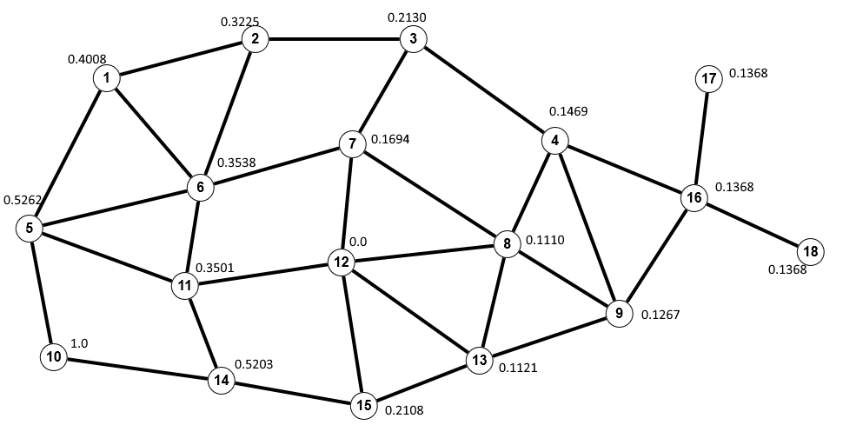
Legt man, um noch ein weiteres Beispiel zu zeigen, den Ausgang in den Knoten 17 und die Falle nach 18 (oder umgekehrt), errechnet sich für jeden Startknoten (natürlich außer 17 und 18) die Wahrscheinlichkeit von $\frac{1}{2}$, was leicht einzusehen ist, denn die Entscheidung, ob man den Ausgang findet oder in die Falle geht, entscheidet sich erst und genau im Knoten 16, und da ist sie eben $\frac{1}{2}$. Und tatsächlich wird auch das Anlegen einer Sperre richtig berechnet, d.h. für die Falle in Knoten 16 und den Ausgang in 17 (oder 18) werden alle Wahrscheinlichkeiten (außer 17) zu 0.0 berechnet.
In der Anlage ZWProc.mw findet sich eine in Maple geschriebene Prozedur, die die Berechnung der Wahrscheinlichkeiten vornimmt. Die Adjazenzmatrix wird aus einer txt.Datei eingelesen (Elemente wie in obigem Beispiel $A$ angeordnet).
ZWProc.mw
In [3] stellt Hochfilzer einen Zusammenhang des Zufallswanderers mit dem Verhalten von Gleichstromkreisen her. Im nächsten Kapitel werde ich dieses Thema aufgreifen, aber allgemein behandeln.
1.4 Gleichstromkreise als Graphen
Im einfachsten Fall sieht ein solcher Stromkreis so aus:
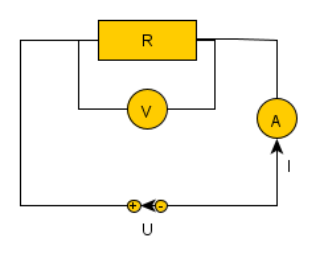
Es gilt das Ohmsche Gesetz $R=\frac{U}{I}$. Strom fließt, deshalb hat er eine Richtung, per Definition von + nach - (technische Stromrichtung), tatsächlich fließen die Elektronen von - nach + (physkalische Stromrichutung); ein Strommessgerät wird deshalb in den Stromkreis an der Stelle integriert, an der man die Stromstärke messen will (es sollte einen möglichst kleinen Innenwiderstand haben). Je nachdem in welcher Richtung man das Gerät polt, zeigt es einen positiven oder negativen Strom an.
Spannung herrscht zwischen zwei Punkten, man sagt, sie fällt an einem Widerstand ab. Zum Messen wird das Spannungsmessgerät an den Punkten angeschlossen, zwischen denen man die Spannung messen will, also nicht in den Stromkreis integriert (Das Spannungsmessgerät sollte einen möglichst hohen Innenwiderstand haben).
Rechenbeispiel:
$U=5 [V], R = 10 [\Omega].$ Wie groß ist die Stromstärke? Antwort: $I=\frac{U}{R} [\frac{V}{\Omega}] = 0.5 [A].$
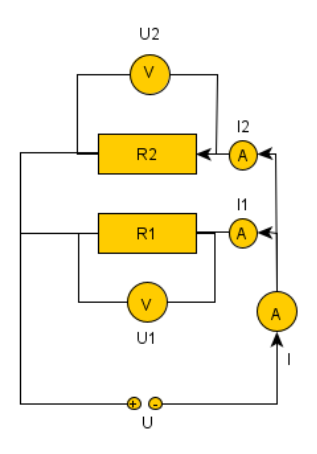
Mit den vorhandenen Bauelementen kann man den Kreis erweitern. Das erste Bild zeigt eine Reihenschaltung zweier Widerstände, das zweite Bild eine Parallelschaltung.
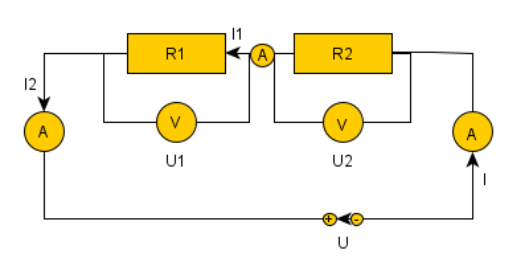
Für die Reihenschaltung gilt, dass sich die Widerstände und die Spannungen, die an den Widerständen abfallen (=von den Messgeräten angezeigt werden) addieren, die Stromstärke ändert sich nicht.
$$ R = R_1 + R_2 \quad U = U_1 + U_2 \quad I = I_1 = I_2$$
Rechenbeispiel:
$U=5 [V], R_1 = 4 [\Omega], R_2 = 6 [\Omega].$ Wie groß ist die Stromstärke und wie groß sind die Spannungsabfälle an den beiden Widerständen? Antwort: $R=R_1 + R_2 = 10 [\Omega], \; I = I_1 =I_2 = \frac{U}{R} [\frac{V}{\Omega}] = 0.5 [A], \; U_1 = R_1 \cdot I_1 [\Omega \cdot A] =2 [V], \; U_2 = R_2 \cdot I_2 [\Omega \cdot A] =3 [V]$ oder auch $ U2 = U - U1 = 3 [V].$
Für die Parallelschaltung gilt, dass sich die Leitfähigkeiten (das ist der Kehrwert des Widerstandes) und die Stromstärken addieren, die Spannung(-sabfall) ist an jedem Widerstand gleich.
$$ \frac{1}{R}= \frac{1}{R_1} + \frac{1}{r_2} \quad I = I_1 + I_2 \quad U = U_1 = U_2$$
Rechenbeispiel:
$U = 5 [V], R_1 = 4 [\Omega], R_2 = 6 [\Omega].$ Wie groß sind die Stromstärken und wie groß ist der Gesamtwiderstand? Antwort: $ \frac{1}{R}= \frac{1}{R_1} + \frac{1}{R_2} = \frac{1}{4} + \frac{1}{6}= \frac{5}{12} \Rightarrow R = 2.4 [\Omega], \; I_1 = \frac{U}{R_1} = \frac{5}{4} [\frac{V}{\Omega}] = 1.25 [A], \; I_2 = \frac{U}{R_2} = \frac{5}{6} [\frac{V}{\Omega}] = 0.83 [A], \; I = I_1 + I_2 = \frac{5}{4} + \frac{5}{6}=2.083 [A].$ Oder auch: $ I = \frac{U}{R} = \frac{5}{\frac{12}{5}}=2.083 [A].$
Soweit die kleine Wiederholung der Grundlagen des einfachen Gleichstromkreises. In vielen technischen Anwendungen ist der Aufbau eines Gleichstromkreises aber ungleich komplizierter. Dazu folgendes Beispiel [5] ohne direkten Anwendungsbezug.

Für solche komplexeren Stromkreise gibt es die beiden Kirchhoffschen Gesetze, auch Knotenregel und Maschenregel genannt - langsam nähern wir uns wieder der Graphentheorie. Knoten sind in obiger Skizze rot eingezeichnet.
Die Knotenregel sagt etwas aus über die Ströme, die an einem Knoten zusammen-/ auseinanderfließen. Betrachten wir in obiger Skizze den Knoten 1; dort "treffen" sich die Ströme $I_1, \; I_2, \; I_6$. Diese Ströme haben alle eine Richtung, die bei der Zeichnung letztlich willkürlich gewählt wurde. Kommt bei der Berechnung ein negativer Wert heraus, so bedeutet dies, dass die Stromrichtung entgegen der eingezeichneten läuft. Die Knotenregelung lautet nun :
$$ \sum_{n=1}^N I_n = 0,$$
was bedeutet, dass sich die (vorzeichenbehafteten) Ströme, die sich in einem Knoten treffen, zu Null aufaddieren. Man muss nur darauf achten, dass man den Strömen bei Aufstellung der Gleichung die richtigen Vorzeichen gibt; ein Strom, der in der Zeichnung in den Knoten hineinfließt bekommt das entgegengesetzte Vorzeichen zu einem Strom, der aus dem Knoten herausfließt. Für Knoten 1 gilt also:
$$I_1 -I_2-I_6=0.$$
Genauso richtig wäre $-I_1 + I_2 + I_6=0$, denn man kann ja eine Gleichung auf beiden Seiten mit der gleichen Zahl (-1) malnehmen.
In gleicher Weise folgt für die Knoten 2 und 3:
$$ I_3 - I_4 - I_7=0 \text{ und } I_4 + I_6 + I_7 - I_5 = 0.$$
Die beiden von mir eingezeichneten Knoten 4 und 5 sind überflüssig, da an ihnen keine Verzweigung der Ströme stattfindet, es gilt insbesondere $I_2 = I_3$.
Die Maschenregel benötigt zu ihrer Formulierung zunächst einmal den Begriff der Masche. An dieser Stelle ist es spätestens sinnvoll, obigen Stromkreis als Graph im Sinne der Graphentheorie zu zeichnen. Unter Weglassung der überflüssigen Knoten 4 und 5 erhält man:

Die Richtung der Kanten zeigt die (angenommene) Richtung der Spannung (Spannungspfeil) an. Üblicherweise zeigen Strom und Spannung in die gleiche Richtung.
Eine Masche ist nun einfach ein Untergraph, der ein Kreis-Graph ist, wenn man den Graphen als ungerichtet betrachtet. Obiger Graph hat somit folgende Maschen:
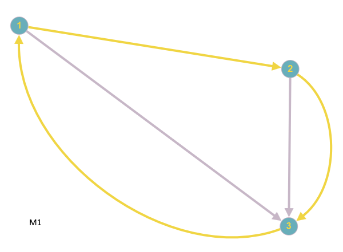

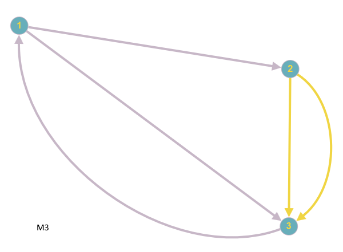
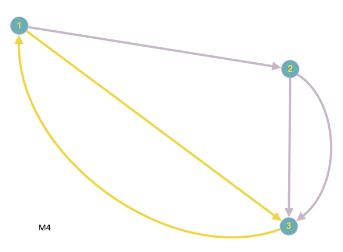
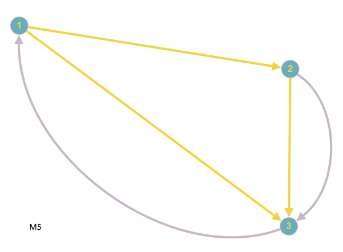
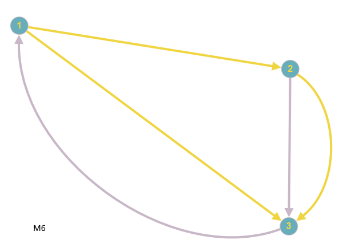
Eine Masche bekommt eine Umlaufrichtung (Maschenpfeil), wobei es egal ist, welche man wählt. Diese Umlaufrichtung dient nun dazu, den Spannungen ein Vorzeichen zu geben. Wenn der Maschenpfeil und der Spannungspfeil die gleiche Richtung haben, wird die Spannung positiv, sonst negativ gesetzt. Die Maschenregel lautet nun:
$$\sum_{n=1}^N U_n = 0.$$
Für die Masche $M_1$ nehmen wir an, dass der Maschenpfeil die Richtung von Knoten 1 nach 2 hat. Dann haben alle Spannungen dieser Masche ein positives Vorzeichen mit Ausnahme von $U_0$, also gilt: $U_1 + U_2 + U_3 + U_7 + U_5 - U_0 = 0$.
Für die Masche $M_2$ nehmen wir an, dass der Maschenpfeil die Richtung 1 nach 2 hat. Dann haben alle Spannungen dieser Masche ein positives Vorzeichen mit Ausnahme von $U_6$, also gilt: $U_2 + U_3 + U_4 - U_6 = 0$.
Für die Masche $M_3$ nehmen wir an, dass der Maschenpfeil die Richtung von Knoten 2 nach 3 hat. Dann gilt: $U_7 - U_4 = 0$.
Entsprechendes kann man für die weiteren Maschen herleiten.
Jetzt haben wir einen Wust von Gleichungen, aber es fehlt schon noch der rote Faden zur Berechnung von Spannungen und Strömen in einem Gleichstromkreis. Insbesondere muss man sich beim Aufstellen der Gleichungen darum kümmern, welche Gleichung linear unabhängig sind und von der Sorte müssen es auch genug sein, damit man das Gleichungssystem lösen kann. Da gibt es gleich 3 Möglichkeiten, die man verwenden kann:
- das Zweigstromverfahren
- das Maschenstromverfahren [4]
- das Knotenpunktpotentialverfahren
Da es mir hier nicht um eine physikalische Vorlesung zur Elektrik geht, greife ich hier nur ein Verfahren heraus, nämlich das Maschenstromverfahren, da es einen weiteren Aspekt der Graphentheorie verwendet. Auch werde ich die Darstellung soweit vereinfachen wie möglich, um das Wesentliche auf das es mir ankommt, herausarbeiten zu können. Den Stromkreis stelle ich wieder als gerichteten Graphen dar, wobei, wie oben, die Richtungen der Kanten den Strom- und Spannungsrichtungen entsprechen. Der Stromkreis hat zwei Spannungsquellen $U_{00}$ und $U_0$, wobei $U_{00}$ so gepolt ist, dass ihr Spannungspfeil in Richtung von $I_5$ zeigt, $U_0$ so, dass ihr Spannungspfeil entgegen der Richtung von $I_0$ liegt.
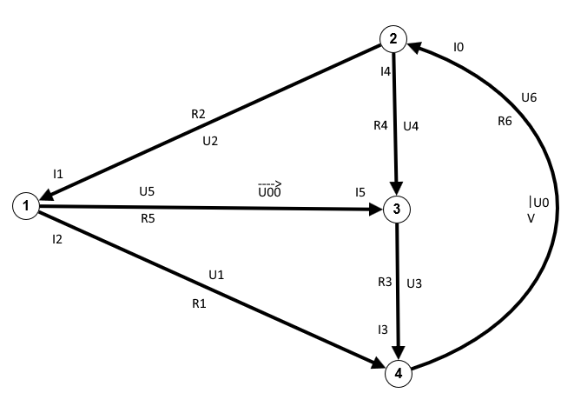
Ähnlich wie bei der Maschenregel muss man als erstes Maschen definieren, in denen dann (gedachte) Maschenströme fließen, die zu Maschengleichungen führen. Die Grundregel bei der Bildung von Maschen lautet, dass jede Kante des Gleichstromgraphen zu mindestens einer Masche angehören muss. Diese Maschengleichungen müssen dann sinnvollerweise linear unabhängig sein, damit man das Gleichungssystem lösen kann. Und jetzt kommt's: Die Wahl der Maschen wird durch die Graphentheorie unterstützt; man bestimmt einen Spannbaum in dem gegebenen (ungerichteten) Graphen. Dies ist ein Untergraph eines zusammenhängenden Graphen, der jeden Knoten im Graphen einmal trifft, also keine Kreise enthält (siehe Kapitel über Bäume). Ein solcher Spannbaum unterteilt dann den Gleichstromgraphen in Maschen, deren Maschengleichungen jedenfalls dann linear unabhängig sind, sofern zu jeder gebildeten Masche genau eine Verbindungskante gehört! Verbindungskante, das ist eine Kante des Graphen, die nicht zum Spannbaum gehört. Diese Bedingung ist allerdings nur eine notwendige Bedingung, d.h. es gibt sehr wohl Systeme von linear unabhängigen Maschengleichungen, bei denen Maschen mehrere Verbindungskanten enthalten, ja, man kann Graphen konstruieren, die keinen Spannbaum enthalten, der obige Einzigkeitsforderung erfüllt. [7]
Ein paar Zahlen können bei der Überprüfung der Wahl des Spannbaumes und der Maschen helfen. Sei $k=|V|$ die Anzahl der Knoten des (ungerichteten) Graphen und $z=|E|$ die Anzahl der Kanten. Dann ist $k-1$ die Anzahl der Kanten des (jedes) Spannbaumes und $z - (k-1)$ die Anzahl unabhängiger Maschengleichungen, die aufgestellt werden können. [6]
Elektrotechnisch ist es egal, welchen Spannbaum man nimmt, wenn er nur den obigen Regeln entspricht, also ein linear unabhängiges Gleichungssystem von Maschengleichungen erzeugt; in unserem Beispiel soll $S=\{\{1,3\}, \{2,3\}, \{3,4\}\}$ der Spannbaum sein. Die Verbindungskanten sind $\{1,2\}, \; \{1,4\}, \; \{2,4\}$. Folgende Bilder zeigen den Spannbaum (rote Kanten), sowie die daraus entstehenden Maschen. ($k=4, z=6 \Rightarrow $ 3 Kanten im Spannbaum, 3 l.u. Maschen, jede Kante gehört zu mindestens einer Masche, die Einzigkeitsregel für die Verbindungskanten ist erfüllt.)
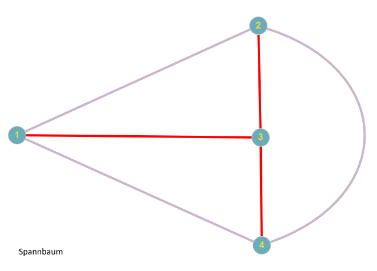
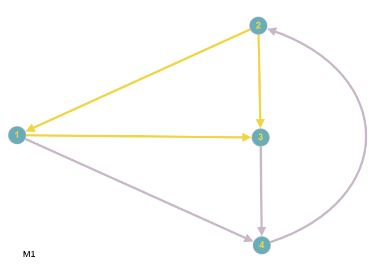
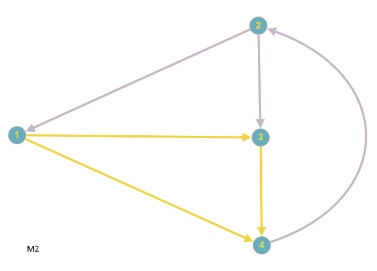
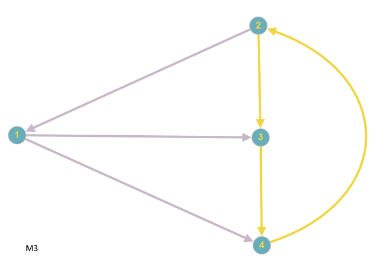
Als (frei wählbare) Stromrichtung (Maschenpfeil) in den Maschen definieren wir: $M_1: \; 1 \rightarrow 2, \; M_2: \; 1 \rightarrow 4, \; M_3: \; 4 \rightarrow 2$ und betrachten den jeweils fließenden Maschenstromes $I_{M_i}$ gleichgerichtet.
Zum Aufstellen eines linearen Gleichungssystems definieren wir nun:
$R_{ii} := $ Summe aller Widerstände ausschließlich in Masche $M_i$.
$R_{ij} := $ Summe aller gemeinsamen Widerstände von Masche $M_i$ und $M_j$. Hierbei ist als Vorzeichenregel zu beachten, dass $R_{ij}$ ein positives Vorzeichen erhält, wenn die beteiligten Maschenströme in die gleiche Richtung zeigen, sonst ein Minuszeichen.
$Uq_{i} :=$ Summe aller Spannungsquellen in Masche $M_i$. Auch hier ist eine Vorzeichenregel zu beachten: Wenn Maschenpfeil und Spannungspfeil der Spannungsquelle entgegengesetzt sind, dann wird ein Plus gesetzt, sonst ein Minus.
Wir fassen zusammen:
$R:=(R_{i,j})$ ist eine (symmetrische) $m \times m$ - Matrix, wobei $m$ die Anzahl der gebildeten Maschen ist.
$IM:=(I_{M_i})^T$ ist ein Spaltenvektor aus $m$ Maschenströmen.
$Uq:=(Uq_{i})^T$ ist ein Spaltenvektor aus $m$ Spannungsquellensummen.
Das zu lösenden Gleichungssystem lautet nun:
$$R \cdot IM = Uq$$
Obiges Beispiel weiterverfolgend, schreibe ich nun die konkreten Werte für $R$ und $U_q$ hin:
$$
R =
\left(
\begin{array}{ccc}
R_2 + R_4 + R_4 & -R_5 & -R_4 \\
-R5 & R_1 + R_3 + R_5 & -R_3 \\
-R_4 & -R_3 & R_6 + R_3 + R_4\\
\end{array}
\right)
\quad
U_q =
\left(
\begin{array}{c}
U_{00}\\
-U_{00}\\
-U_0
\end{array}
\right)
$$
Es bleibt die gewünschten Ströme (und danach auch die Spannungen) aus den gefundenen Maschenströmen zu berechnen. Die Ströme $I_i$, deren Stromzweig nur zu einer Masche gehört, können direkt mit dem zugehörigen Maschenstrom ausgedrückt werden, wobei auch hier wieder gilt, dass bei unterschiedlicher Richtung ein Minuszeichen gesetzt werden muss. Im Beispiel sind die Richtungen aber gleich, also gilt:
$$ I_0 = IM_{M_3}, \; I_1 = IM_{M_2}, \; I_2 = IM_{M_1}$$
Die anderen drei Ströme setzen sich aus mehreren Maschen zusammen, sodass sie durch Addition bzw. Subtraktion der beteiligten Maschenströme berechnet werden müssen (Vorzeichenregel!):
$$ I_3 = IM_{M_3} - IM_{M_2}, \; I_4 = IM_{M_3} - IM_{M_1}, \; I_5 = IM_{M_1} - IM_{M_2}$$
Hurra geschafft!
Zwar ließen sich bei einem 3x3 - Gleichungssystem die Werte für die Ströme noch exakt berechnen, doch ist das Ergebnis länglich und eher uninteressant. Statt dessen gebe ich hier als konkretes Rechenbeispiel nur die Eingabewerte, also Widerstände und Spannungsquellen und die Ergebnisse für die Ströme an.
Rechenbeispiel:
Gegeben: $R1 = 10 [\Omega], \; R2= 5 [\Omega], \; R3 = 20 [\Omega], \; R4 = 15 [\Omega], \; R5 = 5 [\Omega], \; R6 = 10 [\Omega], \quad U_{00} = 10 [V], \; U_0 = 5 [V]$
Berechnet: $IM_{M_1}=I_2=\frac{27}{139} = 0,194 [A], \; IM_{M_2}=I_1= -\frac{53}{139}= -0,381 [A], \; IM_{M_3}=I_0=-\frac{30}{139}=-0,216 [A]$ und
$I_3 = \frac{23}{139}=0,165 [A], \; I_4=-\frac{57}{139}, \; I_5= \frac{80}{139}=0,576[A]$.
Wie im letzten Kapitel bereits angedeutet hat Hochfilzer in [3] einen Zusammenhang zwischen dem Zufallswanderer und Gleichstromkreisen beschrieben. Ich finde dieses Beispiel recht beeindruckend und will es hier auch kurz vorstellen. Insbesondere möchte ich die Berechnung des Gleichstromkreises mit dem gezeigten Maschenstromverfahren durchführen, um auch hier ein weiteres etwas umfangreicheres Beispiel zu haben.
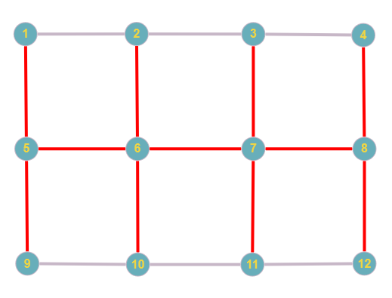
Wir beginnen mit dem Zufallswanderer und schicken ihn in folgenden Irrgarten, daneben die zugehörige Adjazenzmatrix:
![Zufallswanderer, Beispiel aus [3] ZWURIb](../../../_pics/875/ZWURIb.png)

Wie man sieht, ist der Ausgang im Knoten 9 und die Falle im Knoten 12. An den Knoten stehen bereits die Wahrscheinlichkeiten, den Ausgang vor der Falle zu finden, die ich mit ZWProc berechnet habe. Soweit so gut.
Als Gleichstromkreis verwenden wir den gleichen Graphen, erweitert um einen Zweig für eine Spannungsquelle, daneben der Spannbaum.
![Gleichstromkreis aus [3] ZWURId](../../../_pics/877/ZWURId.png)
Zwischen den Knoten, also auf den Kanten (außer zwischen 9 und 12) sollen Widerstände von jeweils $1 [\Omega]$ eingebaut sein, die Spannung $U_0$ betrage $x [V]$. Weiterhin stellen die gerichteten Kanten wie immer die Stromflüsse mit ihrer angenommenen Richtung dar. Wir haben $k=12, z= 18$, woraus folgt, dass der Spannbaum 11 Kanten hat und es 7 Maschen geben sollte, die links auch schon eingezeichnet wurden.
Zwei Dinge fallen auf. Erstens sind die Knoten 1 und 4 eigentlich überflüssig, da hier ja keine Stromverzeigung stattfindet; sie sind aber auch nicht schädlich, vielmehr benötigen wir sie zur Berechnung der Spannungen, die wir an allen 12 Knoten bestimmen wollen. Zweitens erfüllen die Maschen $M_2$ bis $M_7$ die Einzigkeitsregel (nur eine Verbindungskante pro Masche), aber die Masche $M_1$ erfüllt dies nicht. Ich habe auch keinen Spannbaum gefunden, der mit den zugehörigen Maschen die Einzigkeitsregel erfüllen würde. Trotzdem ist das entstehenden Gleichungssystem eindeutig lösbar.
Wir setzen weiter fest, dass die Maschen alle entgegen dem Uhrzeigersinn durchlaufen werden. Mit diesen Informationen können wir nun das Gleichungssystem zur Berechnung der Maschenströme aufstellen. Die Matrix $R$ ist eine $7 \times 7$ - Matrix, die Vektoren $IM$ und $Uq$ haben dementsprechend 7 Elemente.
$$
R:=
\left(
\begin{array}{ccccccc}
3 & -1 & -1 & -1 & 0 & 0 & 0 \\
-1 & 4 & -1 & 0 & -1 & 0 & 0 \\
-1 & -1 & 4 & -1 & 0 & -1 & 0 \\
-1 & 0 & -1 & 4 & 0 & 0 & -1 \\
0 & -1 & 0 & 0 & 4 & -1 & 0 \\
0 & 0 & -1 & 0 & -1 & 4 & -1 \\
0 & 0 & 0 & -1 & 0 & -1 & 4 \\
\end{array}
\right)
\quad
Uq:=
\left(
\begin{array}{c}
x\\
0\\
0\\
0\\
0\\
0\\
0\\
\end{array}
\right)
$$
Die Lösung dieses Systems habe ich mit einem Computeralgebraprogramm (Maple) berechnet; es ergibt sich:
$$
IM =
\left(
\begin{array}{c}
\frac{161}{267}x \\
\frac{67}{267}x \\
\frac{82}{267}x \\
\frac{67}{267}x \\
\frac{25}{267}x \\
\frac{33}{267}x \\
\frac{25}{267}x \\
\end{array}
\right)
$$
Aus den Maschenströmen folgen nun die Ströme an den Kanten des Gleichstromgraphens, z.B. ist $I_0=\frac{161}{267}x = 0,603x.$ Insgesamt erhält man:
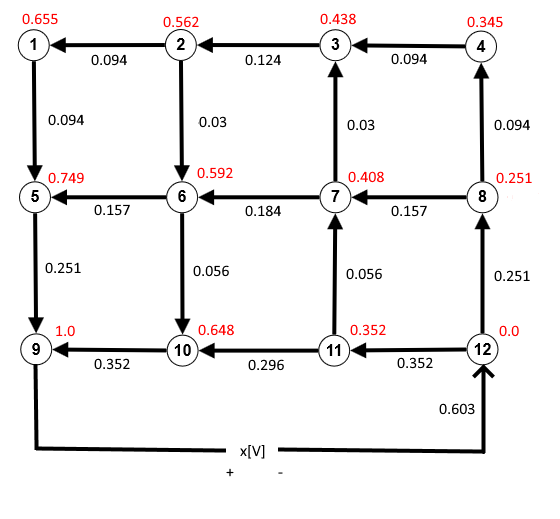
Dabei muss man sich jeden Zahlenwert in obiger Abbildung mit x multipliziert denken. Die schwarzen Werte stellen die Stromstärke in der jeweiligen Kante dar (in $[A]$), dabei habe ich bei den Kanten, die aufgrund des Ergebnisses eine negative Stromstärke hatten, die Richtung geändert. Die roten Zahlen stellen nun die Spannungen (in $[V]$) dar, die an den zugehörigen Knoten gegen Null gemessen werden, also misst man beispielsweise am Knoten 4 eine Spannung von $0.345\cdot x [V]$ gegenüber dem Konten 12 (oder dem Minuspol der Spannungsquelle). Wie berechnet man nun diese Spannungen. Ganz einfach: da zwischen Knoten 12 und 8 bei $1[\Omega]$ Widerstand ein Strom von $0.251\cdot x [A]$ fließt, liegt nach dem Ohmschen Gesetz zwischen 12 und 8 eine Spannung von $0.251\cdot x [V]$ und zwischen 8 und 4 eine Spannung von $0.094\cdot x [V]$ an. Das ergibt zusammenaddiert eine Spannung von $0.345\cdot x [V]$. Auch hier ist die Richtung der Kanten zu berücksichtigen! Will man z.B. die Spannung zwischen 12 und 5 berechnen, so addieren sich die Werte von 12 bis 9 zu 1.0 auf und dann muss man wegen der entgegengerichteten Kante von 9 bis 5 den Wert 0.251 abziehen. (Hätte ich die Kanten bei negativem Strom nicht umgekehrt, wäre es vielleicht noch augenfälliger gewesen.)
Ja, die roten Spannungsfaktoren sind genau die Wahrscheinlichkeiten des Zufallswanderers. Zufall? Nein natürlich nicht. Das ist es ja gerade, worauf Hochfilzer hinaus wollte: Hier wird das gleiche Stück Mathematik auf zwei völlig verschiedene Aufgabenstellungen angewendet und liefert korrespondierende Ergebnisse. Und Hochfilzer setzt noch einen drauf: Die Wege des Zufallswanderers sind Beispiele für Markovketten, einem Teilgebiet der Stochastik.
In einem kleinen Anhang habe ich eine tiefergehende Begründung über dieses "gleiche Stück Mathematik" (über harmonische Funktionen) beschrieben.
Harmonisch.pdf
2 Von v nach w, Wege durch Graphen
Definiton 2.1 (Weg, Pfad, Zyklus, Kreis, Eulerweg-/kreis, Hamiltonweg-/kreis, Kantenfolge) [8]
Sei $G = (V,E)$ Graph (egal ob gerichtet oder nicht, egal ob Mehrfachkanten vorkommen) und $W=(v_1, \cdots, v_n)$ ein n-Tupel von Knoten aus $V$, sodass für alle $i \in \{1, \cdots, n-1\}$ gilt:
- $\{v_i, v_{i+1}\} \in E$, falls $G$ ungerichteter Graph ohne Mehrfachkanten ist
- $(v_i, v_{i+1}) \in E$, falls $G$ gerichteter Graph ohne Mehrfachkanten ist
- $E(\{v_i, v_{i+1}\}) > 0$, falls $G$ ungerichteter Graph mit Mehrfachkanten ist
- $E((v_i, v_{i+1})) > 0$, falls $G$ ungerichteter Graph mit Mehrfachkanten ist.
$v_i$ und $v_{i+1}$ sind also jeweils durch eine Kante verbunden. $W$ nennt man ungerichteten Weg, wenn $G$ ungerichtet ist, gerichteten Weg, wenn $G$ gerichtet ist. $v_1$ heißt Startknoten, $v_n$ Endknoten des Weges. Als Weglänge bezeichnen wir die Anzahl der Kanten des Weges.
Ein Weg $W$ heißt
- Pfad, wenn die $v_i$ paarweise verschieden sind
- Zyklus, wenn Startknoten und Endknoten gleich sind ($v_1=v_n$)
- Kreis, wenn nur Startknoten und Endknoten von $W$ gleich sind (oder auch: $v_1 = v_n$ und $(v_1, \cdots, v_{n-1})$ einen Pfad bilden)
- Eulerweg, wenn $W$ ein Weg ist, der alle Kanten des Graphen $G$ genau einmal enthält
- Eulerkreis, wenn $W$ ein Zyklus ist, der alle Kanten des Graphen $G$ genau einmal enthält (Kein Kreis, Knoten dürfen mehrfach vorkommen!)
- ein zusammenhängender Graph, der einen Eulerkreis besitzt heißt eulerscher Graph
- Hamiltonweg, wenn jeder Knoten des Graphen $G$, genau einmal durchlaufen wird
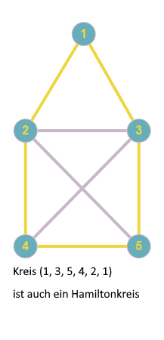
- Hamiltonkreis, ein Zyklus, bei dem jeder Knoten des Graphen $G$ genau einmal durchlaufen wird.
Bei Wegen, Pfaden, Zyklen und Kreisen ist es egal, welche Kante in einem Multigraphen von Knoten zu Knoten benutzt wird, da die Definition nur Knoten beinhaltet.
Eine Kantenfolge ist eine Abfolge von Knoten und Kanten, die abwechselnd aufeinander folgen und deren Kanten immer die beiden benachbarten Knoten enthalten. Formaler:
Kantenfolge $= v_1, e_1, v_2, e_2, \cdots, e_{n-1}, v_n$ mit $e_i=\{v_i,v_{i+1}\}$ für alle $i=1..n-1$. Kanten und Knoten können sich innerhalb einer Kantenfolge wiederholen. Ein Kantenzug von $v_1$ bis $v_n$ impliziert die Existenz eines Weges von $v_1$ nach $v_n$.


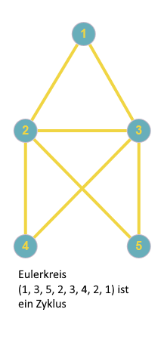
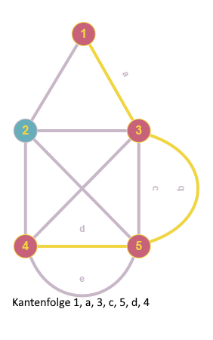
Bemerkung 2.2
Ein Hamiltonkreis ist ein Hamiltonweg, ein Eulerkreis ist ein Eulerweg, ein Kreis ist ein Zyklus, ein Pfad ist ein Weg.
Für Eulerwege und Eulerkreise gibt es einen wesentlichen Satz, der eulersche Graphen charakterisiert. Er stellt einen Zusammenhang zum Grad der Knoten eines Graphen her.
Satz 2.3 (Euler-Hierholzer) [10]
Sei $G$ ein ungerichteter, zusammenhängender Graph. Dann sind folgende Aussagen äquivalent:
- $G$ ist ein eulerscher Graph
- jeder Knoten in $G$ hat geraden Grad
- die Kantenmenge von $G$ ist die Vereinigungsmenge aller Kanten von paarweise disjunkten Kreisen.
Einen analogen Satz gibt es für gerichtete Graphen. Hierholzer hat auch einen Algorithmus zum Auffinden von Eulerkreisen entwickelt.
Korollar 2.4
Ein ungerichteter, zusammenhängender Graph enthält genau dann einen Eulerweg, wenn zwei oder keiner seiner Konten von ungeradem Grad sind. Gibt es in $G$ keinen Knoten mit ungeradem Grad, ist der Eulerweg sogar ein Eulerkreis.
Im nächsten Kapitel werde ich Beispiele für die Anwendung dieses Satz vorstellen.
Satz 2.5 (Dirac) [11]
Jeder einfache Graph (ungerichtet, ohne Mehrfachknoten, ohne Schleifen) $G$ der Ordnung $n$ mit Minimalgrad $\delta(g) \geq \frac{n}{2}$ hat einen Hamiltonkreis.
Eng verbunden mit Wegen in Graphen ist die Angabe von Kantengewichten, die meistens einen konkreten Anwendungsbezug haben, z.B. als Entfernungen zwischen den Knoten oder als Kosten bei der Nutzung der Kanten. Diese Gewichte können durchaus auch negativ sein. Kantengewichte sind durch die bereits definierte Kantengewichtsfunktion (Def. 1.11) gegeben.
Eine interessante erste Aufgabenstellung zu Wegen in Graphen ist die Frage nach der Anzahl von Wegen von einem Knoten i zu einem anderen Knoten j. Betrachten wir dazu einerseits den folgenden ungerichteten Graphen mit Mehrfachkante [20]:
 ---^3-->
---^3--> 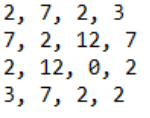
Wieviele verschiedene Wege der Länge 3 gibt es in diesem Graphen?
Andererseits kann man auch in einem gerichteten Graphen ohne Mehrfachkanten die Frage stellen:
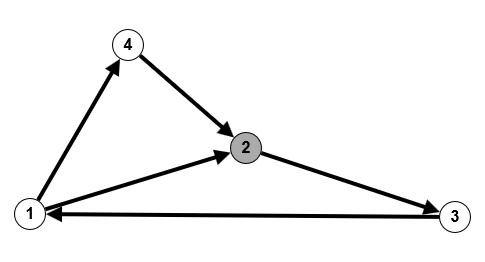
 ---^3-->
---^3--> 
Wieviele verschiedene Wege der Länge 3 gibt es in diesem Graphen?
Der folgende Satz beantwortet beide Fragen auf die gleiche Weise.
Satz 2.6 (siehe Satz 1.15g)
a) Sei $G$ ein ungerichteter Graph mit Mehrfachkanten und A die zugehörige Adjazenzmatrix. Dann ist $A^n(i,j)$ die Anzahl der Wege in $G$ von i nach j.
b) Sei $G$ ein gerichteter Graph ohne Mehrfachkanten und A die zugehörige Adjanzenzmatrix. Dann ist $A^n(i,j)$ die Anzahl der Wege in $G$ von i nach j.
Die obigen Abbildungen enthalten rechts neben der Adjazenzmatrix auch ihre 3ten Potenzen. Sie beantworten die gestellten Fragen. Man entnimmt beispielsweise, dass es im obigen Graphen keinen Weg der Länge 3 von Knoten 3 nach Knoten 3 gibt, aber 12 von Knoten 3 nach Knoten 2. Dies ist auf den ersten Blick erstaunlich, da ein Weg von 3 nach 2 (oder auch von 2 nach 3) nicht über 4 und 1 gehen kann, denn dann wäre der Weg zu lang (aber sehr wohl über 4 oder 1). Das bedeutet, es muss allein zwischen 2 und 3 12 Möglichkeiten geben, unterschiedlich zu gehen. Dies liegt natürlich daran, dass es zwischen 2 und 3 eine Mehrfachkante gibt und die Kanten ungerichtet sind. Bezeichnen wird die obere Kante zwischen 2 und 3 mit a, die untere mit b, die Kante zwischen 1 und 2 mit c und die zwischen 2 und 4 mit d. Der jeweilige Rückweg erhält ein Minuszeichen. Dann finden wir folgende Wege zwischen 2 und 3:
(a -a a), (b -b b), (a -a b), (b -b a), (a -b b), (b -a a), (a, -b a), (b -a b), (c -c a), (c -c b), (d -d a), (d -d b)
Andererseits reduzieren gerichtete Graphen die Anzahl der Wege deutlich, da ja ein Hin und Zurück auf der gleichen Kante nicht möglich ist (wenn es nicht einen Hin- und Zurück-Pfeil gibt). In unserem unteren Beispiel tritt erst bei der 5ten Potenz der Adjazenzmatrix (also Weglänge 5) eine Weganzahl von 2 auf. Es ist der Weg von 1 nach 2: $1 \rightarrow 4 \rightarrow 2 \rightarrow 3 \rightarrow 1 \rightarrow 2$ und $1 \rightarrow 2 \rightarrow 3 \rightarrow 1 \rightarrow 4 \rightarrow 2$.
Ich greife hier noch einmal die in Satz 1.15i definierte Erreichbarkeitsmatrix auf. Durch Addition der Potenzen einer Adjazenzmatrix (beginnend bei 0, endend bei n) und Setzen aller positiven Werte auf 1 bekommt man nacheinander die Erreichbarkeit des Knotens j von i aus durch einen Weg der Länge n angezeigt.
Für den ungerichteten Graphen erhält man die Folge:
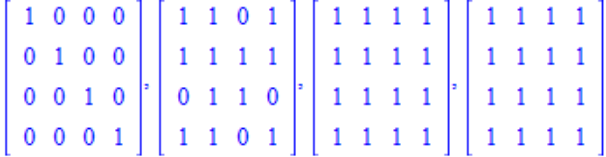
für den gerichteten Graphen:

Damit ist in beiden Fällen die komplette Erreichbarkeit gewährleistet, wenn man im ersten Beispiel mindestens Wege bis zur Länge 2 zulässt, im zweiten Fall Wege bis zur Länge 3.
Ein Beispiel, bei dem nicht die Erreichbarkeit aller Knoten untereinander vorhanden ist, kann man dem folgenden Graphen entnehmen; die Folge der Erreichbarkeiten ist in blau dargestellt.
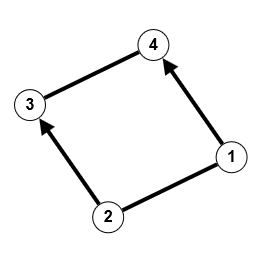

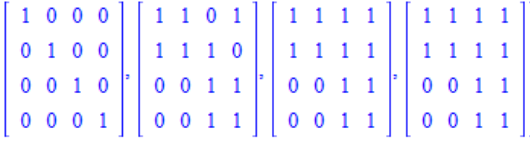
Entsprechend ist der gezeichnete gerichtete Graph nur schwach zusammenhängend.
Auch bei nicht zusammenhängenden Graphen sollte die Erreichbarkeitsmatrix zeigen, welche Knoten nicht miteinander verbunden sind. Das Beispiel hinter Satz 1.18 mit 7 Knoten liefert folgende Erreichbarkeitsfolge:

Die Knoten 3 und 4 sind von den anderen separiert, bilden also eine eigene Zusammenhangskomponente. Somit hat man hier eine andere Methode um zu zeigen, dass ein Graph nicht zusammenhängend ist (neben der Reduzibilität der Adjanzenzmatrix).
Als letztes in diesem Kapitel noch eine Aussage über die Anzahl von Pfaden in einem vollständigen Graphen:
Satz 2.6a
Die Anzahl der verschiedenen Pfade der Länge k zwischen zwei beliebigen Knoten in einem vollständigen Graphen $K_n$ ist $\left(\begin{array} {c} n-2 \\ k-1\\ \end{array}\right)\cdot (k-1)!$
2.1 Der Nikolaus in Königsberg
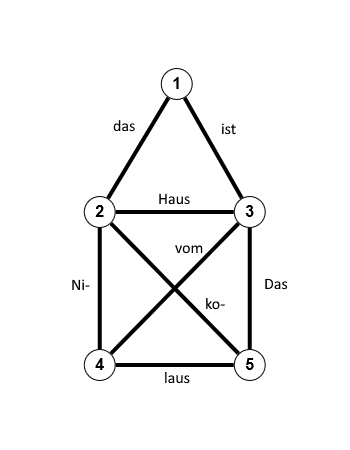
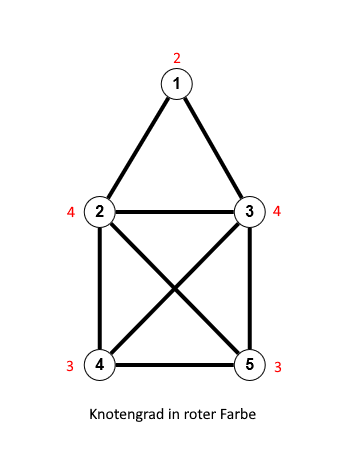
Die gezeigte Lösung ist nicht die einzig mögliche, löst aber die Frage, die mit diesem Haus verbunden ist:
Gibt es einen Eulerweg in diesem Graphen?
Dazu 2 weitere Antworten.
Das Korollar (2.4) zum Satz von Euler-Hierholzer (2.3) gibt eine klare Antwort: Es existiert ein Eulerweg (aber kein Eulerkreis), denn genau 2 Knoten haben einen ungeraden Grad (siehe obige Abbildung).
Die zweite Antwort ist mit der Frage verbunden, wie man einen Eulerweg findet. Ich will hier nicht auf allgemeine Algorithmen zur Findung von Eulerwegen oder -kreisen eingehen, sondern nur an diesem Beispiel einen kleinen Algorithmus vorstellen, den ich vor einiger Zeit mal als Übung zu einem rekursiven Java-Programm geschrieben habe. Die Eingabe in das Programm verlangt die Angabe der Ecke, wo der Eulerweg beginnen soll und gibt entweder den Eulerweg aus oder einen Hinweis, dass es keinen gibt.
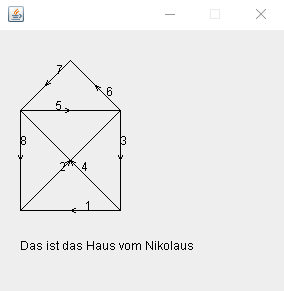
Wir sehen, dass dieser Weg ebenfalls im Knoten 5 beginnt, aber anders verläuft im ersten Bild, was zeigt, dass ein Eulerweg nicht eindeutig sein muss, selbst wenn er am gleichen Knoten startet.
Diese Ausgabe wird auch bei einem Startknoten "rechts oben" , also 3 und "links oben" also 2 angezeigt. Es fällt auf, dass gerade die Knoten mit geradem Grad keinen Eulerweg zulassen, die ungeraden aber doch. Dies ist leicht zu verstehen, denn wenn man an einem Knoten mit geradem Grad startet und alle Kanten durchlaufen will, dann kommt man nach der letzten Kante dieses Knotens nicht mehr von diesem Knoten weg. WEG - HIN - WEG - HIN für Knoten vom Grade 4. Wenn man hofft, in der Zwischenzeit alle anderen Kanten durchlaufen zu haben, hätte man einen Eulerkreis gefunden, den es aber nicht gibt.
Wen's interessiert, ich habe das kleine Programm mit Programmtext und ausführbarem Code in eine .zip-Datei gepackt; sie kann über den folgenden Link heruntergeladen werden.
Nikolaus.zip
Das nächste Beispiel ist nicht nur klassisch, es ist auch historisch. Die Stadt Königsberg hat 7 Brücken über den Fluß Pregel, die in folgendem Graphen den Kanten entsprechen; die Knoten stellen eine Insel (4) bzw. Ufer des Flusses dar:

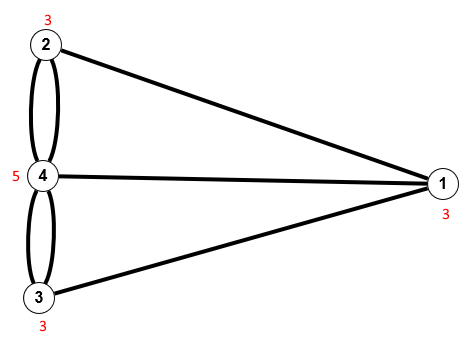
Der Mathematiker Leonhard Euler hat sich 1736 der Fragestellung angenommen, ob es einem Weg gibt, bei dem man alle Brücken genau einmal überquert und ob es einen ebensolchen Rundweg gibt, bei dem man wieder am Ausgangspunkt ankommt. Euler hat im Satz 2.3/2.4 die Implikation entdeckt, die aus der Existenz eines Eulerweges in einem Graphen folgt, dass es maximal 2 Knoten ungeraden Grades geben darf (die andere Richtung hat Hierholzer beigesteuert). Damit folgt sofort, dass es keinen Eulerweg und damit auch keinen Eulerkreis geben kann, denn wie man sieht, haben alle 4 Knoten einen ungeraden Grad. Euler war mit dieser Entdeckung einer der Begründer der Graphentheorie.
2.2 Kurz und knapp
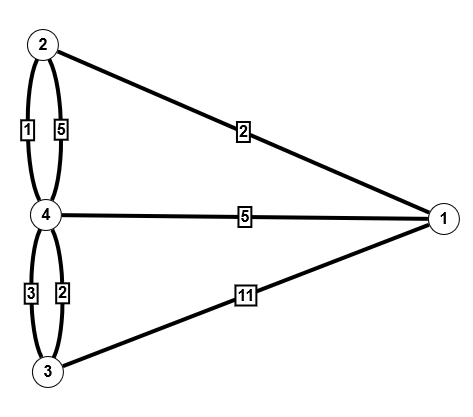
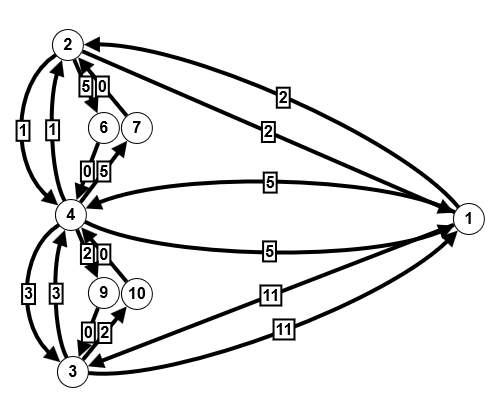
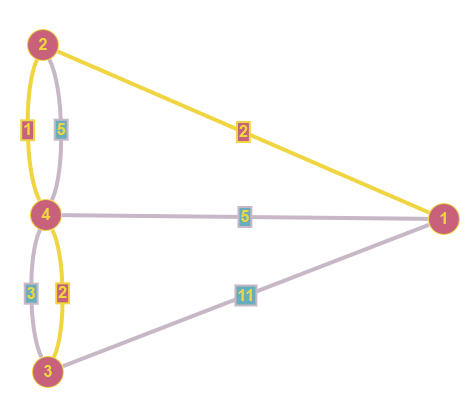
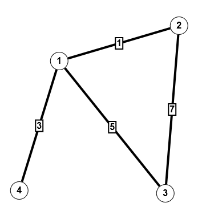
Obiger Graph auf der linken Seite zeigt, wie viel das Passieren der Brücken kostet. Wir nehmen mal an, wir möchten von 1 nach 3 (also von einer Insel auf das Ufer der Pregel). Der direkte Weg über die Brücke für 11 Kreuzer ist natürlich nicht der günstigste. Anstatt alle Wege durchzuprobieren (was bei der geringen Größe des Graphen möglich wäre), gibt es verschiedene Algorithmen, die solche Probleme lösen. Zu den bekanntesten gehört der Algorithmus von Dijkstra (1959), auf den ich später noch ausführlicher eingehen werde. Aber ich will ihn hier schon einmal anwenden. Der Algorithmus erlaubt keine negativen Gewichte, die in anderen Anwendungen durchaus vorkommen können, ist für gerichtete Graphen gedacht und unterstützt keine Multigraphen. Aber der Brückengraph ist ein ungerichteter Multigraph wegen der doppelten Kanten zwischen 2 und 4 bzw. 3 und 4. Wie bei der Einführung der unterschiedlichen Graphentypen bereits erwähnt, kann man aber ungerichtete Graphen in gerichtete Graphen und einen Multigraphen durch Einfügen zusätzlicher Knoten in einen Graphen ohne Mehrfachkanten überführen. Das Ergebnis sieht man im zweiten Bild, das leider schon nicht mehr allzu übersichtlich ist. Das dritte Bild zeigt das Ergebnis unserer Fragestellung mit Dijkstra berechnet, bei dem ich wegen der besseren Übersichtlichkeit in der Zeichnung wieder auf den ungerichteten Multigraphen zurückgegangen bin. Der kostengünstigste Weg geht also vom Knoten 1 aus und führt über 2 und 4 nach 3, wobei man noch die richtigen Brücken auswählen muss und zahlt dann 5 Kreuzer. Das ist weniger als die Hälfte des direkten Weges, aber man muss auch doppelt so weit laufen.
Nehmen wir jetzt zusätzlich an, dass es Brücken, gibt, die nur in einer Richtung benutzt werden können (Einbahnstraßen), dann erkennt der Dijkstra auch dies richtig und schlägt den optimalen Weg vor.
Links der Weg von 1 nach 3, rechts der Rückweg (billiger wegen der Einbahnstraße).
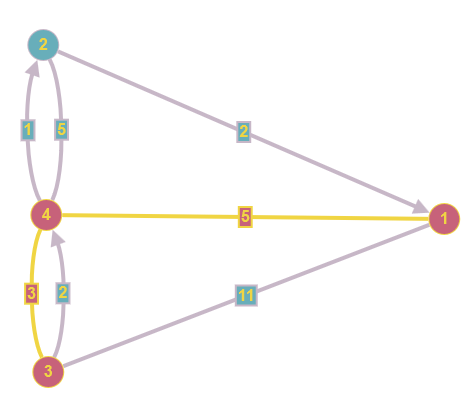
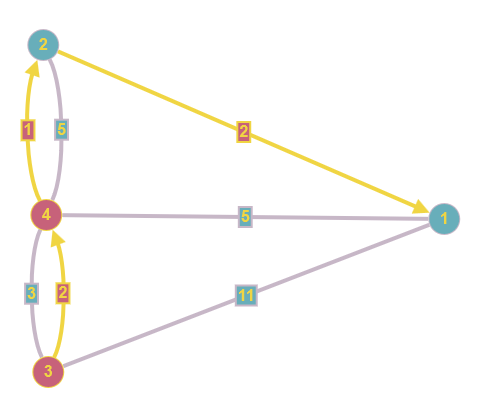
Die typische Anwendung des Dijkstra ist die Routenplanung. Hier bedeuten die Kantengewichte die Entfernung zwischen zwei Knoten, die Kanten sind die Straßenverbindungen. Tatsächlich berechnet der Algorithmus nicht nur den optimalen Weg zwischen gewünschtem Anfangs- und Zielknoten, sondern er berechnet vom Angangsknoten aus die günstigsten Wege zu allen (Ziel-)Knoten des Graphen. Dann sucht man sich den zutreffenden Weg für den gewünschten Zielknoten und die Distanz heraus. Dieses Vorgehen ist recht aufwändig, wenn man sich vorstellt, dass ist einem deutschen oder gar europäischen Straßennetz ein optimaler Weg gefunden werden soll. Allerdings gibt es Verbesserungen des Algorithmus, die dieses Problem in den Griff bekommen.
Auch ohne das "Verkomplizieren" eines Mulitigraphen zu einem ohne Mehrfachkanten vornehmen zu müssen, gibt es ebenfalls Verbesserungen des Dijkstra-Algorithmus (siehe z.B. [12]).
Für die Einschränkung, dass Dijkstra keine negativen Kantengewichte zulässt, kann man dies durch einen anderen Algorithmus, den von Bellman und Ford, umgehen. Er lässt auch negative Kantengewichte zu und erkennt sog. negative Zyklen. Es ist gar nicht so einfach, Anwendungsbeispiel zu finden, die negative Kantengewichte benötigen, denn dass beim Durchlaufen einer Kante negative "Kosten", also ein "Gewinn" anfällt, ist schon ungewöhnlich. Trotzdem habe ich zwei Beispiele gefunden, die ich hier vorstellen will, zusammen mit einer Realisierung des Bellman-Ford in Maple.
Das erste Beispiel hat einen schönen Bezug zu sehr aktuellen Themen dieser Zeit (2022), nämlich die Einführung von Elektroautos, also batteriebetriebenen Fahrzeugen mit Elektromotor. Die Frage der Reichweite solcher Autos ist ein zentrales Thema bei der Entscheidung, ob man sich ein solches Auto anschafft. Gegenüber den Verbrennern haben eAutos neben anderem einen wesentlichen Unterschied, nämlich die Möglichkeit der Energierückgewinnung bei Bergabfahrten (und auch beim Verzögern, was wir aber hier außer Betracht lassen). Nun ist es aber aus technischen und physikalischen Gründen nicht so, dass man bei einer Bergabfahrt genauso viel Energie zurückgewinnen könnte, wie bei einer auf gleicher Strecke vorgenommenen Bergauffahrt gebraucht wird. Man wird also in einem Graphen, der den Energieaufwand darstellt, jeweils zwei Kanten unterschiedlicher Richtung von Knoten A nach Knoten B eintragen, deren Kantengewichte bei positiver Steigung positiv und bei negativer Steigung negativ sind. Der Absolutwert des negativen Gewichtes ist im allgemeinen kleiner als der des positiven. Die Frage, wie man an solche Daten kommt, diskutiere ich hier besser nicht; vielmehr habe ich einen kleinen Graphen vorbereitet, der eine fiktive Geographie darstellt.
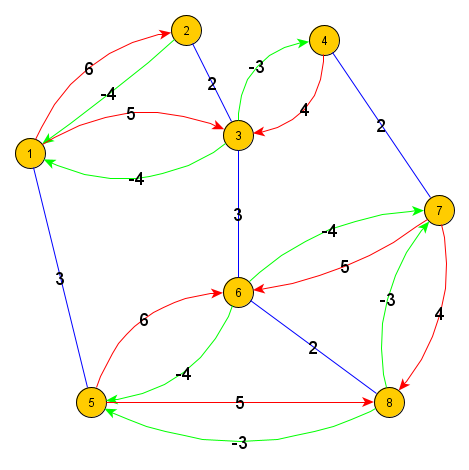

Die Knoten 2, 3, 6 und 8 stellen einen Höhenzug dar, zu dessen beiden Seiten das Land abfällt. Die roten Kanten sind Steigungen mit positiven Gewicht, die grünen haben ein negatives. Wegstrecken, die (fast) keine Steigung/Gefälle haben, benötigen natürlich auch Energie, sie sind in blau und ungerichtet gezeichnet, obwohl sie natürlich zwei gegengerichtete Kanten mit gleichem Gewicht darstellen. Neben dem Graphen steht die zugehörige Adjazenzmatrix für gerichtete, gewichtete Graphen, die für jede Kante das Gewicht zeigt oder Null, wenn es keine Verbindung gibt.
Was tut nun der Algorithmus von Bellman und Ford?
Wie auch bei Dijkstra gibt es einen Anfangsknoten und es werden die "Kosten" für die Wege zu allen anderen Knoten (den Zielknoten) berechnet. Für jeden Knoten des Graphen wird in einer Tabelle der momentane Wert des bisher kürzesten Weges eingetragen und der Vorgänger auf diesem Weg. Dieses Durchforsten des gesamten Graphen muss $n(G)-1$ - oft erfolgen, wie man zeigen kann, dann ist man erst mal soweit durch und hat ein vorläufiges Ergebnis.
In dem beigefügten Maple-Programm werden diese Informationen in zwei Matrizen der Größe $n(G)-1 \times n(G)$ abgelegt. Die Anzahl der Zeilen ist so groß wie die Anzahl der Durchläufe zur Durchforstung des Graphen. Es ist eigentlich nicht notwendig alle Zwischenergebnisse zu behalten, es würde immer nur das letzte reichen. Aber um die Entwicklung der Zwischenergebnisse sehen zu können, habe ich sie aufbewahrt.
KD ist die Matrix der Distanzen. Sie wird in der ersten Zeile mit Unendlich initialisiert, außer der Wert, der zum Anfangsknoten gehört, er wird auf Null gesetzt. M.a.W. die Distanz vom Anfangsknoten zu allen anderen Knoten ist zunächst einmal unbekannt ($\infty$), die zu ihm selbst natürlich 0.
$KD[1, \cdot] = (\infty, \infty, \infty, \cdots, 0.0, \cdots, \infty)$, 0.0 steht an der Stelle $s$, Nummer des Anfangsknotens.
Das Programm benutzt statt Unendlich die große Zahl $10^{99}$, es sei $n := n(G)$.
KD := Matrix(n - 1, n);
KD[1, s] := 0.;
for j from 1 to n do
if j <> s then KD[1, j] := 1.0*10^99; end if;
end do;
KV ist die Matrix der Vorgängerknoten. Sie braucht nicht initialisiert zu werden:
KV := Matrix(n - 1, n)
Das Durchforsten des Graphen erfolgt nun $n-1$ mal und das für jede Kante des Graphen. Wenn in der Adjazenzmatrix eine Kante vorhanden ist (<>0) wird die Prozedur CheckEdge aufgerufen. Der zweite Teil des folgenden Snippets speichert eine fertige Zeile in KD bzw. KV in die nächste Zeile.
KV := Matrix(n - 1, n);
for k from 1 to n - 1 do
for i from 1 to n do
for j to n do
if A[i, j] <> 0 then
CheckEdge(i, j, k);
end if;
end do;
end do;
if k <> n - 1 then
for l from 1 to n do
KD[k + 1, l] := KD[k, l];
KV[k + 1, l] := KV[k, l];
end do;
end if;
end do;
Was macht nun CheckEdge? Hier sitzt die zentrale Idee des Algorithmus. Die Prozedur testet für eine Kante, ob die Summe aus Kantengewicht (aus der Adjazenzmatrix) und der bisherigen (kürzesten) Distanz zum Startknoten der Kante (in KD) kleiner ist, als die Distanz zum Endknoten der Kante (in KD); wenn das so ist, dann wird die Distanz zum Endknoten neu bewertet, also gleich der berechneten Summe aus Kantengewicht und Distanz zum Startknoten der Kante gesetzt. Außerdem wird in diesem Fall als Vorgänger des Endknotens der Startknoten eingesetzt.
CheckEdge:=proc(i,j,k);
# Kantentest nach BellmanFord
global KD, KV, A;
local g;
g:=A[i,j]+KD[k,i];
if g < KD[k,j] then
KD[k,j]:= g;
KV[k,j]:=i;
end if;
end proc;
Hier das Ergebnis für den eAuto-Graph mit dem Anfangsknoten 8.
$$
KD = \left(
\begin{array}{cccccccc}
\infty & \infty & \infty & 4 & -3 & 2 & -3 & 0 \\
0 & \infty & 5 & -1 & -3 & 2 & -3 & 0 \\
0 & 6 & 3 & -1 & -3 & 2 & -3 & 0 \\
-1 & 5 & 3 & -1 & -3 & 2 & -3 & 0 \\
-1 & 5 & 3 & -1 & -3 & 2 & -3 & 0 \\
-1 & 5 & 3 & -1 & -3 & 2 & -3 & 0 \\
-1 & 5 & 3 & -1 & -3 & 2 & -3 & 0 \\
\end{array}
\right)
\quad
KV=
\left(
\begin{array}{cccccccc}
0 & 0 & 0 & 8 & 8 & 8 & 8 & 0 \\
5 & 0 & 6 & 7 & 8 & 8 & 8 & 0 \\
5 & 1 & 4 & 7 & 8 & 8 & 8 & 0 \\
3 & 3 & 4 & 7 & 8 & 8 & 8 & 0 \\
3 & 3 & 4 & 7 & 8 & 8 & 8 & 0 \\
3 & 3 & 4 & 7 & 8 & 8 & 8 & 0 \\
3 & 3 & 4 & 7 & 8 & 8 & 8 & 0 \\
\end{array}
\right)
$$
Was zeigen nun diese beiden Matrizen? KD enthält in jeder Zeile die momentanen Kosten (am Ende die geringsten Kosten) für einen Weg vom Anfangsknoten zum Zielknoten. Natürlich ist die Spalte des Anfangsknotens konstant 0 (hier die achte Spalte). KV erlaubt eine Bestimmung welcher Weg für welchen Zielknoten (bei ja festem Angangsknoten) der optimale ist. Man beginnt beim Zielknoten und hangelt sich rückwärts von Vorgänger zu Vorgänger durch den Weg bis man am Anfangsknoten angekommen ist. Beginnen wir z.B. bei Knoten 2; dessen Vorgänger ist 3, dessen 4, dessen 7 und dessen 8. Also ist der beste Weg von 8 nach 2: 8, 7, 4, 3, 2; die Gesamtkosten dieses Weges sind 5.
Man erkennt außerdem, dass sich ab der vierten Durchforstung nichts mehr ändert, man könnte also in einer Optimierung des Programmes Schluss machen, wenn man dies erkennt.
Nach spätestens $n-1$ Durchforstungen ist das Endergebnis erreicht, d.h. eigentlich könnte man jetzt zufrieden sein, was bedeutet, dass jede weitere Durchforstung des Graphen nichts Neues mehr bringt. Aber! Es gibt Graphen mit negativen Kantengewichten, bei denen das nicht so ist. Sie können sog. negative Zyklen enthalten, d.h. einen Zyklus bei dem die Summe der Kantengewichte negativ ist. Mann könnte also diesen Zyklus immer wieder durchlaufen, was in unserem Beispiel mit dem eAuto einen beliebigen Energiegewinn mit sich bringen würde. Das kann aber nicht sein (jedenfalls in diesem Beispiel). Zum besseren Verständnis dazu ein kleiner Beispielgraph.
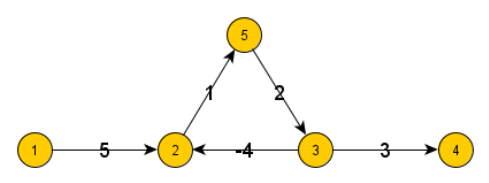

Der negative Zyklus ist hier $2 \rightarrow 5 \rightarrow 3 \rightarrow 2$; er hat eine Kantensumme von -1. Will man jetzt also von 1 nach 4 könnte man bei 3 immer wieder in Richtung von 2 abbiegen und würde so immer weiter Kosten sparen, ja sogar etwas herausbekommen. Um diese Situation zu erkennen, lässt Bellman-Ford die Durchforstung ein weiteres Mal durchlaufen. Wenn bei dieser n-ten Durchforstung wiederum eine Kostenverminderung irgendeines Knotens erfolgen würde, liegt ein negativer Zyklus vor.
Unser Programm löst dies so:
CheckNeg:=proc(i,j,k);
# Test auf negative Zyklen
global KD, KV, A;
local g;
g:=A[i,j]+KD[k,i];
if g < KD[k,j] then
printf("%s%d%s%d","Negativer Zyklus bei ",i, ", ",j);
end if;
end proc;
Das Programm liefert bei Anwendung auf diesen Graphen mit negativem Zyklus bei dem Anfangsknoten 1 die Fehlermeldung:
"Negativer Zyklus bei 2, 5"
Der negative Zyklus wird also beim Prüfen der Kante $(2,5)$ entdeckt.
Mann kann den Eindruck gewinnen, dass negative Zyklen einfach einen Fehler im Aufbau des Graphen darstellen, quasi ein Verstoß gegen den "Energieerhaltungssatz". Es gibt aber doch auch Beispiele, in denen die Detektion eines negativen Zyklus das gewünschte Ergebnis darstellt. Dazu habe ich in [13] ein Beispiel gefunden, das wohl eine Aufgabe einer Übung zur Graphentheorie zu sein scheint. Es handelt sich um das gegenseitige Verhältnis von Währungskursen. Auch hier gilt, schon mal vorab bemerkt, das beim Tauschen von Währungen der "Energieerhaltungssatz" verletzt wird. Die Aufgabe macht folgende Annahmen zu Umtauschkursen:
- 1 US-Dollar erbringt 46,4 indische Rupien
- 1 indische Rupie erbringt 2,5 japanische Yen
- 1 japanischer Yen erbringt 0,0091 US-Dollar
Als Graph sieht das so aus:
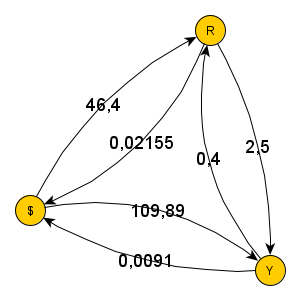
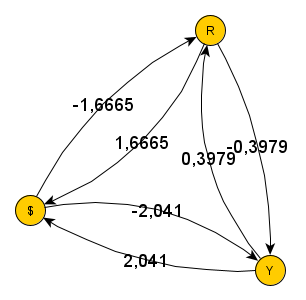

Damit kann man aber noch nichts anfangen, denn die Wechselkurse können ja nicht addiert werden, sondern man muss sie multiplizieren, wie das obige Rechenbeispiel zeigt. Hier hilft aber ein kleiner Trick. Wenn man das Ziel hat, Zyklen aufzuspüren, die einen Umtauschgewinn versprechen, nennen wir sie Arbitrage-Zyklen, muss man aus der Multiplikation eine Addition machen; das kann der Logarithmus. Und um negative Zyklen zu erhalten geht man bei den Wechselkursen zuvor noch zu den Kehrwerten über, denn der Logarithmus einer Zahl kleiner 1 ist bekanntlich negativ.
$$
\log(\frac{1}{46,4}) + \log(\frac{1}{2,5}) + \log(\frac{1}{0,0091})=\log(\frac{1}{46,4}\cdot \frac{1}{2,5} \cdot \frac{1}{0,0091})=\log(\frac{1}{1,0556}) < 0
$$
Das mittlere Diagramm zeigt den umgerechneten Graphen, rechts daneben die Adjazenzmatrix. Natürlich erkennt man den negativen Zyklus auch ohne Programm, aber es beruhigt, dass das Programm mit dem Bellmann-Ford Algorithmus dies auch tut. Wenn der Graph nun erheblich mehr Wechselkurse enthält, dann ist dies nicht mehr so offensichtlich und man ist froh, das programmtechnisch lösen zu können. In der Realität ist es natürlich so, dass Wechselkurse einem stetigen Wandel unterliegen, was bedeutet, dass ein negativer Zyklus keinen allzu langen Bestand haben dürfte.
Das Maple-Programm habe ich als Sheet in folgendem Link hinterlegt. Es ist natürlich nicht nur auf das Beispiel für eAutos beschränkt, sondern ist ein allgemeiner Bellman-Ford Algorithmus, der als Eingabe nur die Adjazenzmatrix in einer .txt-Datei und den Anfangsknoten benötigt.
eAuto.zip
Zum Abschluss dieses Kapitels möchte ich noch einen Algorithmus vorstellen, der ebenfalls "kürzeste Wege" berechnet, dies aber für alle Knotenpaare in einem Graphen tut, es ist der Algorithmus von Floyd und Warshall. Er setzt ebenfalls einen gerichteten, gewichteten Graphen ohne Mehrfachkanten voraus und lässt aber sogar negative Kantengewichte zu, aber mit der Einschränkung, dass man sicher sein muss, keine negativen Zyklen zu haben, d.h. er erkennt sie nicht, sondern liefert dann ein falschen Ergebnis. Historisch ist die Berechnung der Kosten der optimalen Wege Floyds Anteil und die Bestimmung des Weges im Graphen der von Warshall.
Um deutlich zu machen, welchen Vorteil dieser Algorithmus bietet, habe ich zwei Beispiele:

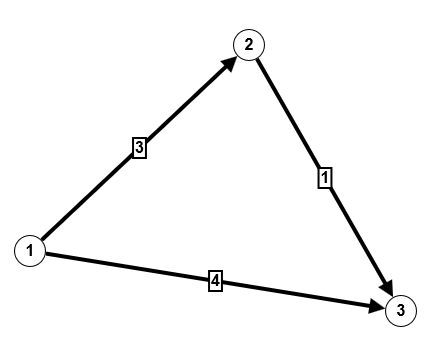

Das erste Bild zeigt den Ausgangsgraphen an, das zweite das Ergebnis von Floyd-Warshall und das dritte die sog. Distanzmatrix. Bild 2 zeigt, dass der kürzeste Weg von 1 nach 3 nicht der direkte sein kann, sondern über 2 führen muss; dann gewinnt man Kosten in Höhe von einem Punkt gegenüber dem direkten Weg. Die Distanzmatrix stellt die geringsten Kosten nochmals dar und zeigt auch, welche Knoten im Graphen nicht miteinander verbunden sind.
Etwas weniger langweilig ist das nächste, leicht modifizierte Beispiel. Wir fügen eine weitere Kanten von 3 nach 1 ein:
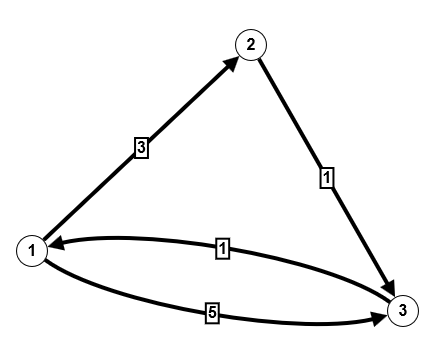
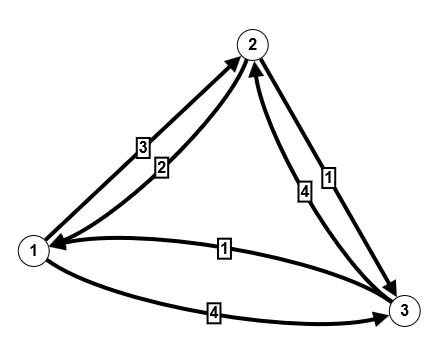

Plötzlich gibt es auch Rückwege zwischen 1 und 2 bzw. 2 und 3, d.h. der Algorithmus kann auch dafür benutzt werden, herauszubekommen, ob es überhaupt einen Weg von A nach B gibt und welcher der kostengünstigste ist. Wir sehen:
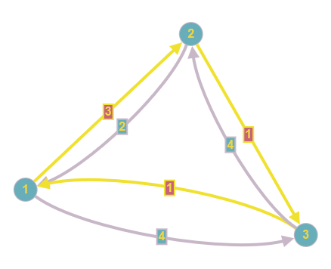

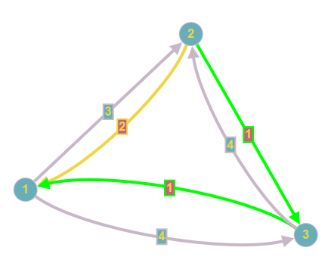
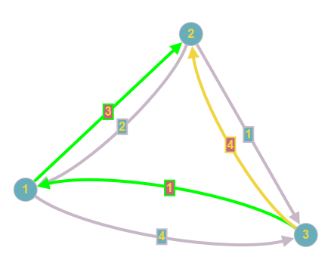
Die gelben Kanten im ersten Bild sind unverändert zum Ursprungsgraph und stellen die kürzesten Wege dar. Im zweiten Bild ist die gelbe Kante auch die gleiche wie vorher, aber sie hat ein geringeres Gesamtgewicht, d.h. der Weg führt über Knoten 2 (grüne Kanten). Bild 3 und 4 zeigen, dass es auch Wege von 2 nach 1 und von 3 nach 2 gibt, nämlich über die grünen Kanten.
3 Man sieht den Wald vor Bäumen nicht
Definition 3.1 (planar)
Ein Graph G=(V,E) heißt planar, wenn er in einer Ebene so dargestellt werden kann, dass sich keine zwei Kanten schneiden.
Diese Definition ist zwar sehr anschaulich, aber nicht gerade von großer Exaktheit geprägt. Andererseits benötigt man zu einer exakteren Definition den Begriff der Jordankurve aus der elementaren Differentialgeometrie (jede Kante ist eine solche Kurve in der Ebene, die sich nur an Knoten schneiden können). Dieses Fass will ich hier nicht aufmachen und belasse es deshalb bei der anschaulichen Definition. Bisher haben wir intuitiv angenommen, dass die Graphen in der Ebene gezeichnet werden und Kreuzungen zweier Kanten haben uns nicht gestört. Vielfach kann man durch anderes Zeichnen der Kanten eine Überschneidung umgehen; wenn das aber nicht geht, dann ist der Graph nicht planar. Dazu eine kleine Denksportaufgabe, die allgemein bekannt ist, aber gut zur Graphentheorie und planaren Graphen passt.
Drei Energieversorgungswerke, ein Wasserwerk, eine Elektrizitätswerk und ein Gaswerk sollen mit drei Häusern über Leitungen verbunden werden, ohne dass sich die Leitungen schneiden. Man zeichnet dazu ein Bild, das die Verhältnisse erklären soll.
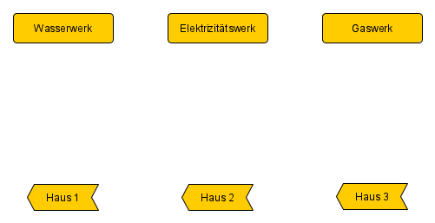
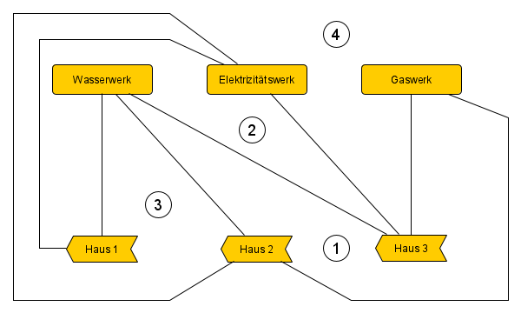
Bei dem Versuch, die Leitungen auf dem Papier zu zeichnen, findet man keine Lösung. Die letzte Leitung, die man zeichnen will, schneidet immer eine andere. Im rechten Bild fehlt die dritte Leitung vom Gaswerk zu Haus 1.
Dazu kann man drei Bemerkungen machen.
- Es ist tatsächlich unmöglich die Versorgungsleitungen als planaren, zusammenhängenden Graph (in der Ebene) zu zeichnen. Zum Beweis dieser Behauptung gleich mehr.
- Wie bei jeder Denksportaufgabe gibt es auch hier eine gedankliche Barriere, die man zuerst überwinden muss, um zu einer Lösung zu kommen. Hier besteht die Barriere einerseits in der zweidimensionalen Anschauung, die durch die Zeichnung nahe gelegt wird, obwohl das Problem ja eigentlich in der Realität ein dreidimensionales ist. Noch perfider, wenn der Rätselonkel das Bild nicht selber malt, sondern den Rätselrater auffordert, mal ein Bild zu malen. Tatsächlich ist es im Raum kein Problem, ein Schneiden zu vermeiden, indem man eine Leitung über die andere legt, also in die dritte Dimension. Ein Klassenkamerad von mir, kam sogar auf die Idee, das Blatt, auf dem die Zeichnung gemalt war, an einer Stelle zu durchbohren, auf der anderen Seite weiter zu zeichnen und hinter der zu kreuzenden Leitung wieder auf die andere Seite zurückzukehren.
- Betrachtet man die Aufgabe statt auf einer Ebene, auf einer Torusoberfläche, dann ist sie lösbar, auch ohne die Fläche verlassen zu müssen.
Der Beweis, dass der Verbindungsgraph nicht planar sein kann, geht auf einen anderen Satz von L. Euler zurück, der Eulerschen Polyederformel. Eigentlich macht dieser Satz, wie der Name schon sagt, eine Aussage über Polyeder, also räumliche Gebilde, aber man kann ebenfalls zeigen, dass seine Aussage auch für planare, zusammenhängende Graphen gilt.
Satz 3.2 (Eulerscher Polyedersatz für Graphen)
Für jeden planaren und zusammenhängenden Graphen $G$ gilt: $v - e + g = 2$. Dabei ist $v:= n(G)$, also die Anzahl der Knoten, $e:=m(g)$, also die Anzahl der Kanten und g die Anzahl der Gebiete, die durch den Graphen gebildet werden. Dabei wird das äußere Gebiet mitgezählt.
Bei unserer Denksportaufgabe betrachten wir den Graphen $G := (V,E), \; V:=\{G, L, W\}, \; E:=\{\{G,H_i\},\; \{L,H_i\},\; \{W,H_i\} | i=1 \cdots 3\}$.
$v$ und $e$ sind bekannt, d.h. wir können $f$ berechnen, wenn wir indirekt annehmen, dass $G$ planar ist. $v=6, \; e = 9, \; \rightarrow f = 5 \qquad (*)$.
Jedes Gebiet in diesem Graphen wird von 4 oder 6 Kanten begrenzt, denn- 2 Kanten können es nicht sein, denn dann würde ein Haus von einem Werk mit 2 Leitungen versorgt
- mehr als 6 Kanten können es nicht sein, da es nur 6 Knoten gibt
- eine ungerade Anzahl von Kanten (also 1, 3 oder 5) kann es nicht sein, da bei einer Kante eine Schleife vorläge, bei 3 oder 5 Kanten zwei Häuser oder zwei Werke miteinander verbunden sein müssten.
Also kann man rechnen, dass bei 5 Gebieten die kleinste mögliche Anzahl von Kanten
$$
\frac{4+4+4+4+4}{2} = 10
$$
wäre, was die tatsächliche Zahl von 9 übersteigt (durch 2 muss dividiert werden, da eine Kante immer an zwei Gebiete grenzt). Somit gibt es keinen planaren, zusammenhängenden Graphen mit obigen Vorgaben. Das obige rechte Bild zeigt 4 Gebiete, es müssten 5 sein, aber das klappt eben nicht. [3]
Die oben schon einmal bemühte elementare Differentialgeometrie kennt den Begriff der Euler-Poincare-Charakteristik. Darunter versteht man die Zahl $ \chi_S := v - e + g$, die charakteristisch für eine geschlossene Fläche S ist, die man (immer) mit einem Dreiecksnetz überziehen (triangulieren) kann und dann die Anzahl der Knoten, Kanten und Gebiete zählt. Die Charakteristik ist von dem Aussehen der Triangulation unabhängig, eben ein Charakteristikum für S. Auch für die Ebene gibt es diese Zahl, sie ist wie in obigem Satz bereits gesagt gleich 2; gleiches gilt übrigens für die Kugeloberfläche, was bedeutet, dass das GEW-Problem auch nicht auf einer Kugeloberfläche lösbar ist. Aber es gibt auch andere Oberflächen, z.B. hat der Torus eine Oberfläche, die eine Charakteristik von Null hat. Berechnet man wie oben (*) für den Torus die Anzahl der Gebiete, so erhält man $f=3$. Mit den gleichen Argumenten wie oben hat ein Gebiet 4 oder 6 begrenzende Kanten. Nimmt man als Maximum 6 Kanten je Gebiet, überschreitet man die Anzahl von 9 Kanten nicht, hat also keinen Widerspruch.
$$
\frac{6 + 6 + 6}{2} = 9
$$
Weil nichts Besonderes im Fernsehen kam, haben meine Frau - sie ist Informatikerin - und ich mit Papier und Schere einen Torus gebastelt und so die Dreidimensionalität erzeugt und mit bunten Stiften Werke, Häuser und Leitungen gezeichnet.
Dieses Ergebnis habe ich dann mit einer 3D-Grafik in Geogebra gezeichnet:
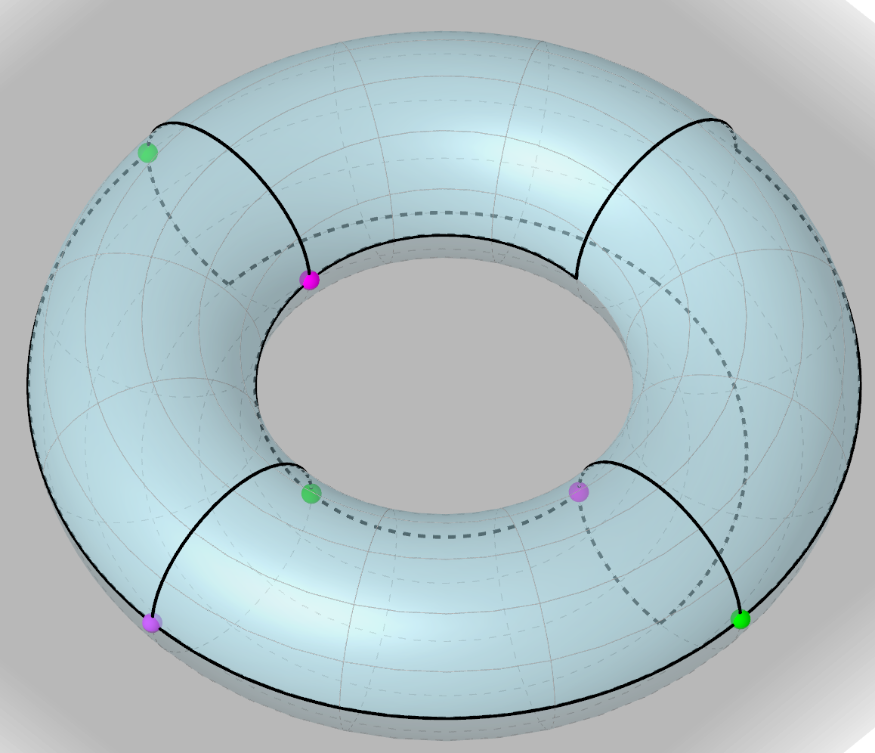
Die violetten Punkt stellen die Werke dar, die grünen die Häuser. Die Anordnung ist natürlich nur exemplarisch zu verstehen. Tatsächlich hat jedes Werk und jedes Haus genau drei Leitungen und die überschneiden sich nicht. Blendet man den Torus aus, erkennt man den Verlauf der Leitungen (= Kanten) noch besser:
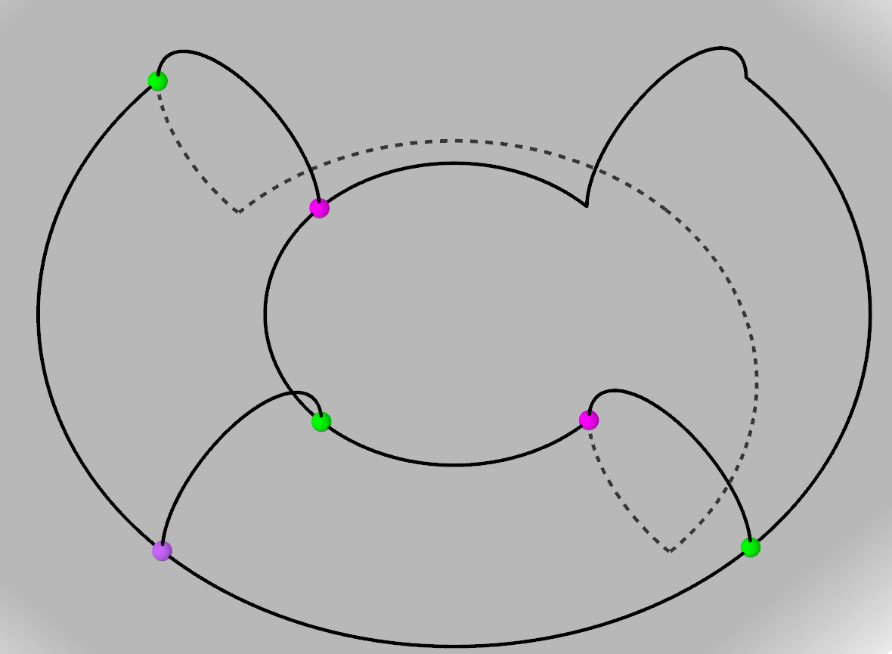
Das Bild ist so gestaltet, dass man sieht, dass genau eine Linie (die gestrichelte) unterhalb des Torus verläuft; man kann sich vorstellen, dass dies auf der Ebene oder der Kugeloberfläche dem "Tunnel" entspricht, der die neunte nicht schneidende Verbindung möglich macht. Betrachtet man die Kanten als Gummibänder, kann man die Werke und Häuser so verschieben, dass sie jeweils nebeneinander liegen und hat dann ein ähnliches Bild wie in der Ebene. Welche drei Gebiete bilden sich denn nun durch die Kanten? Die drei folgenden Bilder zeigen die Umrandungen der Gebiete, jedes Gebiet hat 4 Kanten. Auch hier habe ich den Torus ausgeblendet.
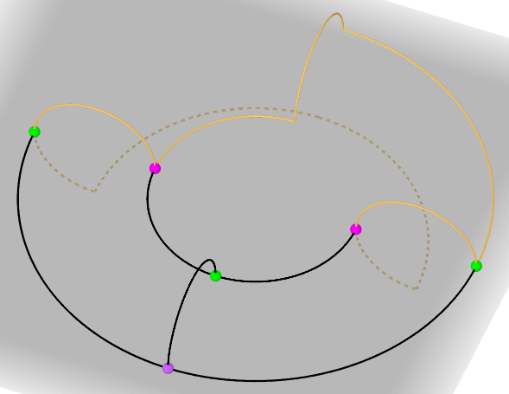
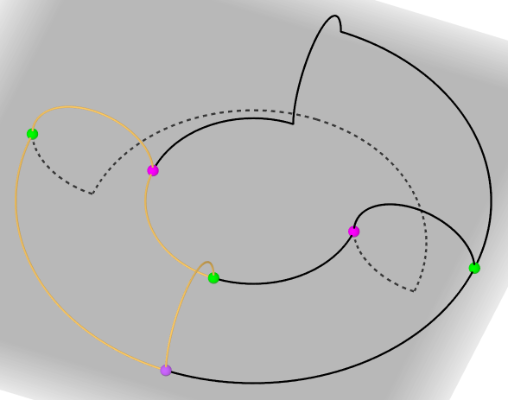
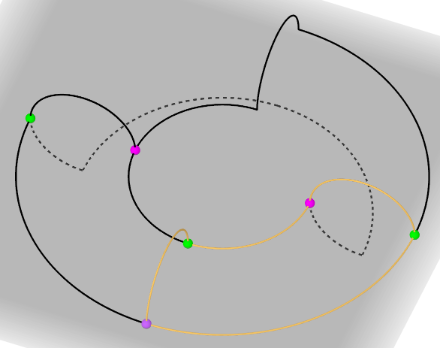
Nach diesem Ausflug in die Eulersche Polyeder-Formel eine Definition, die zentrale Definition dieses Kapitels.
Definition 3.3 (Wald, Baum, binärer Baum, bipartit, Spannbaum, Sterngraph)
Wald $:\Leftrightarrow $ ungerichteter Graph ohne Zyklus
Baum $:\Leftrightarrow $ zusammenhängender Wald (eine Zusammenhangskomponente)
Ein Knoten eines Baumes mit Grad = 1 heißt Blatt.
Binärer Baum $:\Leftrightarrow $ Jeder Knoten eines gerichteten Baumes hat höchstens zwei Nachfolger.
Lineare Liste $: \Leftrightarrow $ Jeder Knoten eines gerichteten Baumes außer dem letzten hat genau einen Nachfolger.
Wurzelbaum $:\Leftrightarrow $ Ein Knoten eines Baumes ist als Wurzel ausgezeichnet.
Die Übertragung dieser Begriffe auf gerichtete Graphen erfolgt durch Zurückführung auf ungerichtete Graphen.
Ein Spannbaum eines ungerichteten Graphen ist ein Teilgraph, der ein Baum ist und alle Knoten des Graphen enthält. (Einen Spannbaum kann es nur in zusammenhängenden Graphen geben.)
Ein Sterngraph ist ein spezieller (Wurzel-)Baum, bei dem alle Kanten von einem Knoten (Wurzel) ausgehen, formal: Ein ungerichteter Graph $S_n=(V,E)$ mit $V = \{v_0, v_1, \cdots, v_n\}$ und den Kanten $E = \{ \{v_0, v_1\}, \{v_0, v_2\}, \cdots, \{v_0, v_n\} \}$ heißt Sterngraph.
Ein einfacher Graph heißt bipartit, falls sich seine Knoten in zwei disjunkte Teilmengen A und B aufteilen lassen, so dass zwischen den Knoten innerhalb A bzw. B keine Kanten verlaufen.
Formal: Sei $G = (V, E), (v, w) \in E $. Dann gilt entweder $v \in A \wedge w \in B \text{ oder } v \in B \wedge w \in A$.
Ein bipartiter Graph heißt vollständig bipartit, wenn jeder Knoten aus $A$ mit jedem Knoten aus $B$ verbunden ist. Bezeichnung: $K_{r,s}$ mit $ r=|A|,\; s=|B|$.
Beispiele für diese Begriffe folgen in den nächsten Kapiteln. An dieser Stelle ein Satz über Eigenschaften obiger Definitionen.
Satz 3.4
a) Jeder Wald ist bipartit.
b) Jeder Wald ist planar.
c) Jeder zusammenhängende ungerichtete Graph mit $n$ Knoten enthält mindestens $n-1$ Kanten.
d) Jeder stark zusammenhängende gerichtete Graph mit $n$ Knoten enthält mindestens $n$ Kanten.
e) Ein ungerichteter Graph ist genau dann zusammenhängend, wenn er einen Spannbaum enthält.
f) Ein gerichteter Graph ist genau dann stark zusammenhängend, wenn seine Adjazenzmatrix irreduzibel ist. Ein ungerichteter Graph ist genau dann zusammenhängend, wenn seine Adjazenzmatrix irreduzibel ist.
g) Jeder Sterngraph ist zusammenhängend.
h) Jeder Sterngraph ist vollständig bipartit, d.h. jeder Knoten aus A ist mit jedem Knoten aus B verbunden, wobei A oder B nur einen Knoten enthält.
Speziell für Bäume gilt weiterhin der folgende Satz:
Satz 3.5 [24]
Folgende Aussagen für einen Graph $G=(V,E)$ sind äquivalent:
a) $G$ is ein Baum
b) Zwischen zwei Knoten von $G$ gibt es genau einen Pfad.
c) $G$ ist zusammenhängend und es gilt $m(G) = n(G) -1$.
d) $G$ enthält keinen Kreis und es gilt $m(G) = n(G) -1$.
e) $G$ ist minimal zusammenhängend (wenn man ein Kante rausnimmt, ist er nicht mehr zusammenhängend).
Und für einen Spannbaum weiß man:
Satz 3.5 (Cayley)
Für einen vollständigen Graphen $K_n$ mit $n$ Knoten gibt es $n^{n-2}$ verschiedene Spannbäume.
Zum Abschluss noch ein Satz über planare Graphen, der eine notwendige Bedingung für Planarität darstellt.
Satz 3.5a [44]
Ein zusammenhängender planarer Graph mit n Knoten ($n \geq 3$) hat höchstens $3n - 6$ viele Kanten.
3.1 Zu bunt?

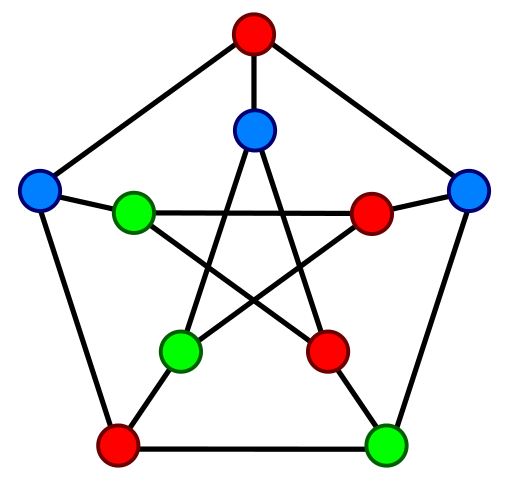
Die Beweise für 5 und 6 Farben waren schon länger bekannt, aber das Vierfarbenproblem erwies sich lange Zeit als harte, ungeknackte Nuss. Interessanterweise gelang der erste Beweis des Vierfarbensatzes in den Jahren 1976/1977 Kenneth Appel und Wolfgang Haken, die mit Hilfe eines Computerprogrammes den Beweis führen konnten. [21] Unter vielen anderen Versuchen wurde auch ein (bisher erfolgloser) Beweisansatz mit der Graphentheorie versucht (Birkhoff 1912). Dazu führt man den Begriff des Chromatischen Polynoms für Graphen ein, deren Knoten gefärbt sind. Das Chromatische Polynom $\chi(G,k)$ ist die Anzahl der Möglichkeiten, die Knoten eines ungerichteten Graphen mit k Farben so zu färben, dass keine zwei verbundenen Knoten die gleiche Farbe haben (siehe rechtes Bild).
Identifiziert man nun die Länder der Landkarte mit den Knoten des Graphen und die Kanten mit der Existenz einer gemeinsamen Grenze, so ist das Vierfarbenproblem äquivalent dazu, dass sich jeder ungerichtete Graph $G$ mit 4 Farben färben lässt, also dass $\chi(G,4) \geq 1$ ist.
Die Forschungen zum Chromatischen Polynom haben einige sehr erstaunliche Aussagen gefunden, die es ermöglichen zu einem gegebenen Graphen das Polynom zu bestimmen. Am Anfang steht die Aussage, dass das Polynom tatsächlich ein Polynom ist. Weiterhin kennt man das chromatische Polynom für mehrere Spezialfälle, für den vollständigen Graphen $K_n$, den Graphen, der nur aus isolierten Knoten besteht, Bäume, Kreise und Sternengraphen. Und dann, ja, dann gibt es noch eine Rekrusionsformel, die man zur Berechnung eines Chromatischen Polynoms in zwei Richtungen verwenden kann. Aber alles nacheinander.
Satz 3.6
Sei $G=(V,E)$ ein ungerichteter, schleifenfreier Graph ohne Mehrfachkanten.
a) Die Anzahl $\chi(G,k)$ der Möglichkeiten die Knoten des Graphen $G$ mit k Farben so zu färben, dass keine zwei verbundenen Knoten die gleiche Farbe haben, ist ein Polynom in k mit ganzzahligen Koeffizienten. Sein Grad ist $n(G)$, sein höchster Koeffizient ist 1.
b) Der Graph, der nur aus n isolierten Knoten besteht, hat das Chromatische Polynom $\chi(G,k)=k^n$.
c) Der vollständige Graph mit n Knoten $K_n$ hat das Chromatische Polynom
$$
\chi(K_n,k) = k \cdot (k-1) \cdot (k-2) \cdots (k-n+1)
$$
Bei $k \leq n-1$ Farben gibt es keine zulässige Färbung von $K_n$. Wenn $k > n-1$, dann sind nur die injektiven Abbildungen $f:V \Rightarrow \{Farbe_1, \cdots, Farbe_k\}$ zulässige Färbungen und das sind gerade $\chi(K_n,k)$ Stück.
d) Jeder Baum $T_n$ der Ordnung n hat das gleiche Chromatische Polynom, nämlich $\chi(T_n,k)=k \cdot (k-1)^{(n-1)}$.
f) Jeder Kreis mit n Knoten hat das gleiche chromatische Polynom, nämlich $\chi(C_n,k)=(k-1)^n + (k-1)\cdot (-1)^n$.
g) Ein Graph $G$ ist genau dann ein Wald der Ordnung n mit m Zusammenhangskomponenten, wenn $\chi(G,k)=k^m\cdot (k-1)^{n-m}$.
h) Bezeiche $G-e$ den Graphen, dem man die Kante $e \in V$ weggenommen hat. Bezeichne $G|e$ den Graphen der entsteht, wenn man eine Kantenkontraktion durchführt, d.h. die beiden Endpunkte von e werden zu einem Punkt verschmolzen; wenn dabei Mehrfachkanten entstehen, werden alle bis auf eine entfernt, s.d. nur eine Kante übrig bleibt.
Mit diesen beiden Bezeichnungen gilt folgende Rekursionsformel:
$$
\chi(G,k) = \chi(G-e,k) - \chi(G|e,k)
$$
i) Für die Zusammenhangskomponenten $G_1, G_2, \cdots, G_m$ von $G$ gilt: $\chi(G,k) = \prod_{i=1}^m \chi(G_i,k)$.
j) Die Koeffizienten der Potenzen von k haben alternierendes Vorzeichen.
k) Sei $a$ Knoten von $G$ mit Grad 1 ($a \in V, \; \deg(a)=1$). Es bezeichne $G':=(v \setminus \{a\}, E \setminus \{a,v\})$, also den Graphen der übrigbleibt, wenn man $a$ und die Kanten von $a$ herausnimmt. Dann gilt: $\chi(G,k) = (k-1)\cdot \chi(G',k)$.
l) Ein Sterngraph hat das chromatische Polynom $\chi(S_n,k) = k\cdot(k-1)^n$.
Definition 3.7
Als Chromatische Zahl $\chi(G)$ eines ungerichteten, schleifenfreien Graphen ohne Mehrfachkanten $G$ bezeichnet man das kleinste k, für das der Graph eine zulässige Färbung mit k Farben zulässt, was dem kleinsten k entspricht, für das $\chi(G,k) \neq 0$ ist.
Satz 3.8 [23]
Für die chromatische Zahl $\chi(G)$ eines ungerichteten, schleifenfreien Graphen $G=(V,E)$ gilt:
a) Ein Graph ist genau dann nicht leer, wenn seine chromatische Zahl größer oder gleich 1 ist.
b) Jeder nichtleere Graph besitzt genau dann die chromatische Zahl 1, wenn er keine Kanten besitzt.
c) Ein Graph ist genau dann bipartit, wenn seine chromatische Zahl kleiner oder gleich 2 ist.
d) Es gilt: $\chi(G) \leq n(G)$.
e) $\chi(K_n) = n$.
f) $\chi(S_n) = 2$.
Will man nun ein chromatisches Polynom berechnen, ist die Rekursionsformel aus Satz 2.7f das Werkzeug der Wahl. Dabei gibt es zwei Strategien. Man formt den Graphen schrittweise so um, dass am Ende nur noch Bäume übrig bleiben, deren Polynome man kennt oder "umgekehrt", man zielt auf vollständige Graphen, deren Polynome ebenfalls bekannt sind. [22] gibt den Hinweis, dass es bei Graphen mit wenigen Kanten die erste Methode, bei vielen Kanten die zweite die effektivere ist. Man beachte, dass die Rekursionsformel in zwei Richtungen verwendet werden kann. So wie sie in f steht, entspricht sie einer Kantenreduktion, stellt man die Formel um, also $\chi(G-e,k)=\chi(G,k) + \chi(G|e,k)$ wird im ersten Summanden eine Kante hinzugefügt. Natürlich ändert sich mit jeder Anwendung $G$.
In speziellen Fällen kann man Satz 2.7 k) zur Berechnung heranziehen. Folgendes kleine Beispiel zeigt eine Anwendung.
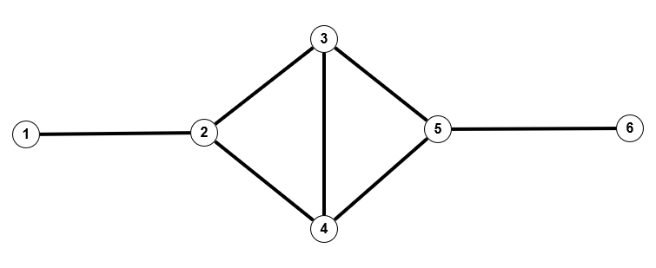 $G$
$G$Die Knoten 1 und 6 haben den Grad 1 und können somit im genannten Satz verwendet werden. Also:
$$
\chi(G,k) = (k-1) \cdot \chi(G_1,k) = (k-1)^2 \cdot \chi(G_2,k)
$$
mit den Graphen $G_1$ und $G_2$:
 $G_1$
$G_1$ $G_2$
$G_2$Nun kommt die Rekursionsformel zum Einsatz und zwar in der Richtung zu vollständigen Graphen, d.h. $G_2$ wird durch Hinzufügen der Kante $\{2,5\}$ zu einem vollständigen Graphen $K_4$ und durch anschließende Kantenkontraktion zu $K_3$. Bei der Kantenkontraktion wird Knoten 2 auf Knoten 5 gelegt (oder auch umgekehrt) und die entstehenden Mehrfachkanten, hier $\{2,3\}$ und $\{2,4\}$, werden weggelassen.
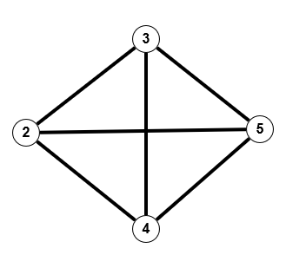 $K_4$
$K_4$  $K_3$
$K_3$Rechnerisch kommt raus:
$$
\chi(G,k) =(k-1)^2 \cdot (\chi(K_4,k) + \chi(K_3,k)) = (k-1)^2 \cdot (k(k-1)(k-2)(k-3) + k(k-1)(k-2)) = k^6 - 7k^5 + 19k^4-25k^3+16k^2-4k=k(k-2)^2(k-1)^3
$$
Ein Programm zur Berechnung eines chromatischen Polynoms habe ich in Pascal (FPC) entwickelt. Bevor ich näher auf das Programm eingehe, möchte ich ein paar Ergebnisse präsentieren. Aus [20] stammt der folgende Graph:
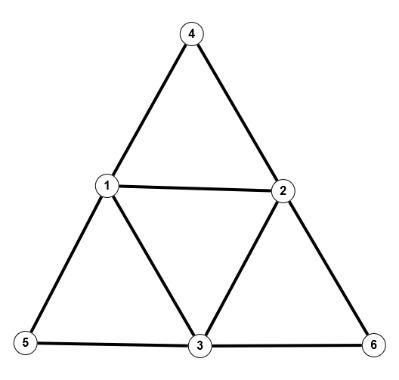

Für das chromatische Polynom gebe ich 3 verschiedene Darstellungen an:
a) Als Linearkombination der chromatischen Polynome der vollständigen Graphen
$$
\chi(G,k) = 1\cdot \chi(K_6,k) + 6\cdot \chi(K_5,k) + 7\cdot \chi(K_4,k) +1\cdot \chi(K_3,k) \qquad (I)
$$
b) Als Linearkombination der Chromatischen Polynome von Bäumen
$$
\chi(G,k) = 1\cdot \chi(T_6,k) -4 \cdot \chi(T_5,k) + 6\cdot \chi(T_4,k) - 4\cdot \chi(T_3,k) + 1\cdot \chi(T_2k) \qquad (II)
$$
c) Als Polynom in k
$$
\chi(G,k) = k^6-9k^5+32k^4-56k^3+48k^2-16k \qquad (III)
$$
d) und als faktorisiertes Polynom
$$
\chi(G,k) = k(k-1)(k-2)^4 \qquad (IV)
$$
Wie man sieht, wechseln die Vorzeichen in (III) alternierend. Die Darstellung in (IV) ermöglicht ein schnelles Bestimmen der chromatischen Zahl, denn für k = 0, 1 und 2 ist $\chi(G,k)=0$, erst für $k=3$ erhalten wir $\chi(G,3) = 6$. Somit braucht man mindestens $\chi(G)=3$ Farben, um den Graphen korrekt zu färben, wie in folgendem Beispiel:

Um eine Visualisierung der einzelnen Rekursionsschritte bei der Berechnung von (I) und (II) zu erhalten, mache man sich klar, dass jeder (Zwischen-)Graph aufgrund der Rekursionsformel in 2 Graphen umgeformt werden muss. Dies ergibt die typische Situation eines binären Baumes, bei dem ja von jedem Knoten maximal zwei Kanten zu weiteren Knoten führen. Die Blätter des fertigen Baumes sind dann vollständige Graphen der Ordnungen n(G) bis 3, bzw. von Bäumen der Ordnungen N(G) bis 2, die man dann nur abzählen braucht, um die Koeffizienten in (I) bzw. (II) zu bekommen.
Die Darstellung mit vollständigen Graphen geht nicht von dem oben abgebildeten Graphen aus, sondern von einem isomorphen Graphen, der bereits vom Aussehen als späterer vollständiger Graph angelegt ist. Die Kanten des binären Baumes sind in grüner Farbe gezeichnet und reichen immer vom Mittelpunkt des Startknotens zur Mitte der Oberkante des Zielknotens.

Folgendes Bild zeigt die Berechnung mit Bäumen als Blätter:

Man kann diese Graphen noch von Hand berechnen, was zwar etwas dauert, aber auch ein gutes Gefühl für den Algorithmus liefert.
Ganz anders sieht das bei dem Graphen oben rechts aus, der übrigens "Petersengraph" heißt und 3-regulär ist. Er hat die Adjazenzmatrix

Diese $10 \times 10$-Matrix in das Programm eingegeben, zeitigt folgende Ergebnisse für den Petersengraph $P$:
a)
$$
\chi(P, k) = 1 \cdot \chi(K_{10},k) + 30 \cdot \chi(K_9,k) + 315 \cdot \chi(K_8,k) + 1435 \cdot \chi(K_7,k) + 2865 \cdot \chi(K_6,k) + 2244 \cdot \chi(K_5,k) + 520 \cdot \chi(K_4,k) + 20 \cdot \chi(K_3,k) \qquad (Ia)
$$
b)
$$
\chi(P,k) = 1 \cdot \chi(T_{10},k) -6\cdot \chi(T_9,k) + 21\cdot \chi(T_8,k) - 56\cdot \chi(T_7,k) + 114\cdot \chi(T_6,k) - 170\cdot \chi(T_5,k) + 180\cdot \chi(T_4,k) -120\cdot \chi(T_3,k) + 36\cdot \chi(T_2,k) \qquad (IIa)
$$
c)
$$
\chi(P, k) = k^{10} - 15 k^9 + 105 k^8 -455 k^7 + 1353 k^6 - 2861 k^5 + 4275 k^4 - 4305 k^3 + 2606 k^2 - 704 k
$$
d)
$$
\chi(P, k) = k(k-1)(k-2)(k^7 - 12 k^6 + 67 k^5 - 230 k^4 + 529 k^3 - 814 k^2 + 775 k -352)
$$
Die chromatische Zahl ist $\chi(P)=3$.
Man sieht an den Koeffizienten der Darstellung (Ia), wie viel vollständige Graphen eine Visualisierung des Entwicklungsbaumes allein haben müsste, ganz abgesehen von den Zwischenschritten. Also verbietet sich sowohl diese Darstellung, als auch eine Berechnung von Hand, was uns wieder zu meinem Pascal-Programm führt.
Es besteht aus 2 Teilen, der erste berechnet die Koeffizienten der vollständigen Graphen (Darstellung (I) oder (II)) und baut einen Baum dieser Berechnung auf. Der zweite Teil macht die graphische Darstellung des im ersten Teil erstellten Baumes. Da die Grundlage der Koeffizientenberechung eine Rekursionsformel ist, liegt es nahe, die zugehörige Programmstruktur ebenfalls rekursiv auszulegen. Dies tut die Prozedur Split, die aus einem (Zwischen-)Graphen gemäß Rekursionsformel zwei neue Graphen erstellt:
procedure Split(A: Matrix; T: PBaum);
type
Ergebnis = record
A: Matrix;
l, m: integer;
newP: PBaum;
end;
var
i, j, n, mE: integer;
Ergplus, Ergminus: Ergebnis;
LastA: Matrix;
{Weitere Prozeduren}
begin
n := length(A);
{Kantenzahl}
mE := 0;
for i := 0 to n - 1 do
for j := 0 to n - 1 do
mE := mE + A[i, j];
mE := mE div 2;
if Wald then
if mE <> n - 1 then
begin
copyA(LastA, A);
Kanteminus(A, T, Ergplus);
Split(Ergplus.A, T^.links);
Kantekontr(LastA, T, Ergplus.l, Ergplus.m, Ergminus);
Split(Ergminus.A, T^.rechts);
end
else
begin
Voll[n - 1] := Voll[n - 1] + T^.Vorz;
end
else
if mE < (n * (n - 1) div 2) then
begin
copyA(LastA, A);
Kanteplus(A, T, Ergplus);
Split(Ergplus.A, T^.links);
Kantekontr(LastA, T, Ergplus.l, Ergplus.m, Ergminus);
Split(Ergminus.A, T^.rechts);
end
else
Voll[n - 1] := Voll[n - 1] + 1;
end;{Split}
Die Prozduren "Kanteminus", "Kanteplus" und "Kantekontr" leisten die Hauptarbeit, die erste löscht eine Kante, die zweite fügt eine Kante hinzu, die dritte legt die zwei Knoten der gelöschten oder eingefügten Kante zusammen, womit mindestens eine Kante wegfällt. Nach jedem Kanteminus, Kanteplus oder Kantekontr ruft Split sich selber wieder auf, was das Absteigen im binären Baum bewirkt. Das Array "Voll" hat am Ende die Ergebnisse, also die gesuchten Koeffizienten der vollständigen Graphen bzw. der Bäume; mit diesen Koeffizienten kann man dann z.B. mit einem Computeralgebraprogramm die endgültigen Polynome berechnen.
In der Prozedur Kanteminus tritt eine zusätzliche Schwierigkeit auf, denn beim Löschen einer Kante kann der Graph in zwei Zusammenhangskomponenten zerfallen. Deshalb wird der Restgraph nach der Löschung einer Kante darauf untersucht, ob er noch zusammenhängend ist; wenn nicht, wird die gelöschte Kante wieder eingebaut und eine andere Kante herausgenommen, bis ein zusammenhängender Graph übrig bleibt und weiterverarbeitet werden kann. Die Kontrolle, ob ein Graph zusammenhängend ist, stellt ein eigenes separates Problem dar, das zu lösen ist. Zwar gibt es gemäß Satz 1.18 ein Kriterium für die Irreduzibilität der Adjazenzmatrix und damit des Zusammenhanges des Graphen, aber man weiß nicht, bis zu welcher Potenz von $A$ man rechnen muss, um eine Aussage zu bekommen; wenn nach 10 Multiplikationen noch kein Ergebnis vorliegt, kann es bei der 11ten Potenz dann doch klappen. Deshalb muss ein anderes Verfahren her. Hier kommt der Spannbaum eines Graphen ins Spiel. Wenn ein Graph einen Spannbaum hat, dann ist er auch zusammenhängend. Es gibt zur Berechnung von Spannbäumen mehrere Verfahren; der in meinem Programm benutzte Algorithmus stammt von Joseph Kruskal, einem amerikanischen Mathematiker. Ich werde ihn in einem eigenen Kapitel vorstellen.
Im zweiten Teil wird der binäre Baum mit Hilfe einer "Breitensuche" durchlaufen, denn die graphische Darstellung soll zeilenweise erfolgen. Das Wort Breitensuche ist insoweit etwas irreführend, als im Baum nicht gesucht wird, vielmehr wird der Baum bis zu seinem Ende durchlaufen, also ein Breitendurchlauf. Da der Graph, der durchlaufen wird, ein Baum ist, also keinen Zyklus hat, kann man bei dem Breitendurchlauf auf die Prüfung verzichten, ob ein Knoten bereits erreicht wurde.
Die Adjazenzmatrix wird aus einer TXT-Datei eingelesen.
Die graphische Ausgabe verwendet, wie schon früher, die in den "Monte Carlo Methoden" erstellte Unit "GraphikUnit", die ihrerseits auf der Unit "graph" des FPC basiert.
Wie immer stelle ich hier das Programm für eigene Versuche zur Verfügung, wie immer ohne jede Gewähr.
ChromPolynom.zip
Und was macht man jetzt mit dem chromatischen Polynom, wenn es denn beim Vierfarbenproblem (bisher) nicht weiter geholfen hat.
Ich habe in [20] eine Anwendung gefunden; die dortige Aufgabe befasst sich mit Ampelsteuerungen an Kreuzungen. Vorgegeben ist eine Kreuzung von 4 Straßen (A, B, C, D) von denen 2 Einbahnstraßen sind.
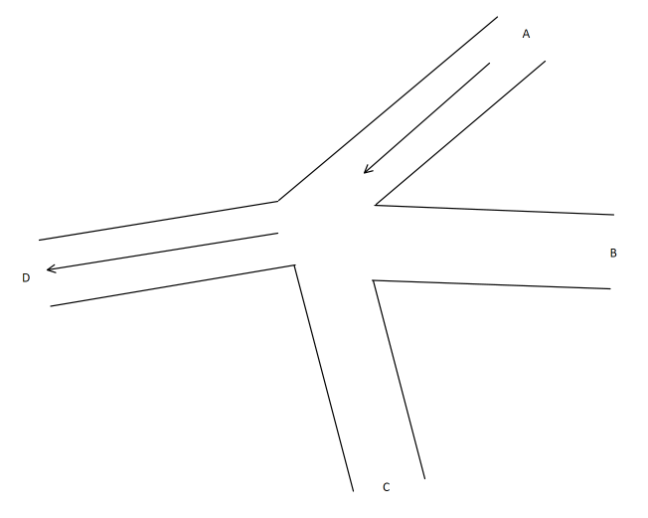
Ziel der Aufgabe ist es herauszufinden, wieviel Grünphasen in einem Ampelzyklus gebraucht werden, um nacheinander alle Fahrzeuge kollisionsfrei über die Kreuzung zu bringen.
Die Lösung erfolgt in 3 Schritten in dem nach folgenden Regeln ein farbiger Graph gebaut wird:
Schritt 1 Knotenbildung:
Ein Knoten entsteht durch zwei Straßen, die zulässiger Weise befahren werden können. Im Beispiel:
AB, AC, AD, BC, BD, CB, CD. Beispielsweise ist BA kein zulässiger Knoten, da man dann gegen die Einbahnstraße fahren müsste.
Schritt 2 Kantenbildung:
Zwei Knoten werden durch eine Kante verbunden, wenn sie nicht gleichzeitig eine Grünphase erlauben, d.h. wenn sie sich auf der Kreuzung beim Abbiegen behindern würden. Im Beispiel:
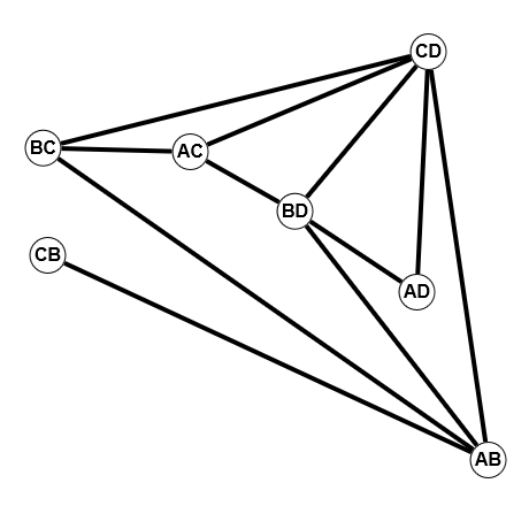

Schritt 3 Chromatische Zahl:
Das Programm berechnet als chromatisches Polynom
a)
$$
\chi(Ampel,k) = 1\cdot \chi(T_7,k) - 4\cdot \chi(T_6,k) + 7\cdot \chi(T_5,k) - 6\cdot \chi(T_4,k) +2\cdot \chi(T_3,k)
$$
b)
$$
\chi(Ampel,k) = k^7 -10k^6 + 42k^5 - 94k^4 + 117k^3 - 76k^2 +20k
$$
c)
$$
\chi(Ampel,k) = k\cdot (k-1)^2 \cdot (k-2)^2 \cdot(k^2-5k+5)
$$
Formel c) weist $\chi(Ampel) = 3$ aus, was in unserem Beispiel 3 Grünphasen innerhalb eines Ampelzyklus bedeutet.
Schritt 4 Färben des Graphen
Um nun herauszubekommen, welche Grünphasen gleichzeitig geschaltet werden können färben wir den Graphen mit 3 Farben eben so ein, dass keine zwei Knoten derselben Farbe miteinander durch eine Kante verbunden sind:
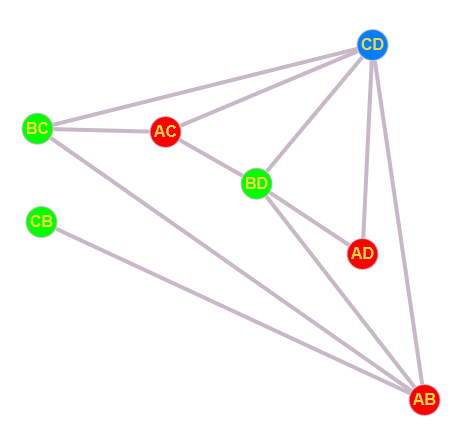
Also können die Fahrspuren AB, AC und AD in der ersten Phase und die Spuren BC, BD und CB in der zweiten Phase gemeinsam geschaltet werden und CD in der dritten (und dies übrigens zusammen mit CB).
Ein anderes Beispiel behandelt die Organisation von Stundenplänen; gemeint ist die Lösung der Frage der möglichen Gleichzeitigkeit von Veranstaltung, z.B. Vorlesungen, für die typischerweise nur eingeschränkte Ressourcen zur Verfügung stehen (Dozenten, Räume, etc.). Zugrunde liege ein festes Zeitraster in das die Vorlesungen einsortiert werden müssen. In der Modellbildung stellen die Vorlesungen die Knoten des Graphen dar, Ressourcenkonflikte die Kanten und die Zeitslots entsprechen den Farben. Ressourcenkonflikt heißt, dass die Veranstaltungen nicht gleichzeitig stattfinden können. Wie im vorherigen Beispiel geht man in 4 Schritten an die Sache heran.
Schritt 1 Knotenbildung
| Vorlesung 1 |
Prof. Dr. Felix Alleswisser |
Großer Hörsaal |
mobile Videowand | |
| Vorlesung 2 |
Prof. Dr. Otto Besserwisser |
Kleiner Hörsaal |
Megaphone | mobile Videowand |
| Vorlesung 3 |
Prof. Dr. Rudi Allesweisserdochnicht |
Großer Hörsaal |
Megaphone | |
| usw. | usw. | usw. | usw. | usw. |
Schritt 2 Kantenbildung
$\{1,2\}$ wegen mobiler Videowand
$\{2,3\}$ wegen Megaphone
$\{1,3\}$ wegen Großer Hörsaal
usw.
Nehmen wir an, dass dadurch folgender Graph entsteht:
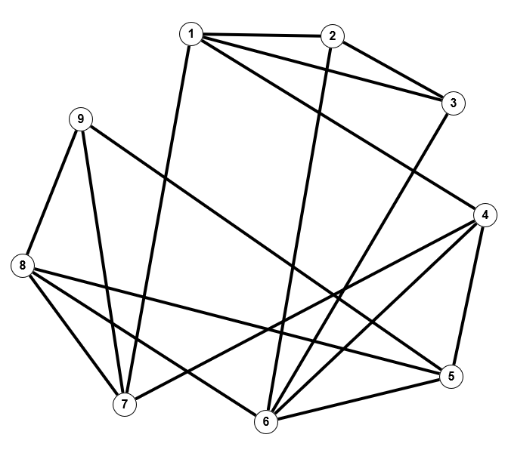

Schritt 3 Chromatische Zahl
Das Programm berechnet folgendes chromatische Polynom:
a)
$$
\chi(StPl,k) = 1\cdot \chi(K_9,k) + 19\cdot \chi(K_8,k) + 115\cdot \chi(K_7,k) + 263\cdot \chi(K_6,k) + 211\cdot \chi(K_5,k) + 46\cdot \chi(K_4,k) + 2\cdot \chi(K_3,k)
$$
b)
$$
\chi(StPl,k)= k^9-17k^8+129k^7-570k^6+1600k^5-2907k^4+3312k^3-2140k^2+592k
$$
c)
$$
\chi(StPl,k) = k(k-1)(k-2)^2(k^5-12k^4+61k^3-165k^2+239k-148)
$$
Somit ist $\chi(StPl)=3$, es reichen also 3 Farben.
Schritt 4 Färben des Graphen
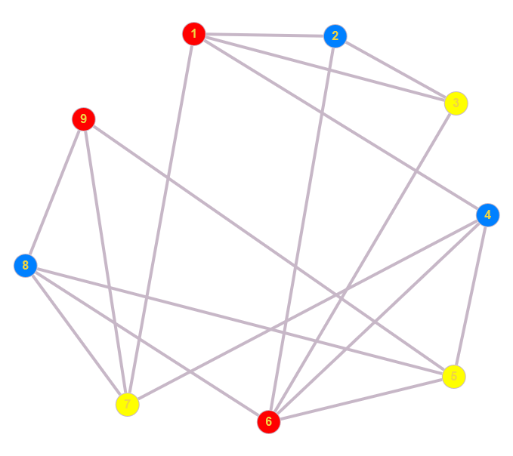
Also können gleichzeitig stattfinden: Vorlesungen 1, 6, 9; 2, 4, 8; 3, 5, 7.
3.2 Unter Spannung
Unter der Fülle von Anwendungen habe ich als erstes eine herausgesucht, die Clusteranalyse heißt, also die "Zusammenballung" von Knoten in einem Graphen bestimmt. [25] Die Idee ist einfach: Die Kantengewichte des Graphen stellen die Entfernungen der Knoten dar und man erhält so einen vollständigen Graphen. Man berechnet zunächst den minimalen Spannbaum des Graphen und löscht dann die Kanten, deren Länge über einem bestimmten Schwellenwert S liegt. Die verbleibenden Zusammenhangskomponenten stellen dann die Cluster des Graphen dar.
Für die Wahl des Schwellenwertes gibt es kein Patentrezept; als ersten, im allgemeinen aber zu kleinen Wert, kann man den Durchschnitt der Kantenabstände des Spannbaumes verwenden und diesen Wert sukzessive vergrößern. Das ausführende Programm erlaubt eine Zeichnung des Clusters mit unterschiedlichen Schwellwerten; aber erst mal muss man natürlich einen Graphen haben, den man untersuchen will. Dazu erzeugt mein Programm zufällig n Knotenpunkte in der Ebene mit Koordinaten (x,y) und berechnet dann die Adjazenzmatrix dieses vollständigen Graphen mit den Abständen als Kantengewichten. Die dem Abstand zugrundeliegende Metrik kann man variieren; betrachten wir zunächst den euklidischen Abstand. Da, wie in der ersten Abbildung dargestellt, die Knotenpunkte zufällig platziert werden, kann man nicht unbedingt eine Haufenbildung erwarten. Folgendes Beispiel zeigt 50 Knoten, links die Ausgangsmenge mit den Knotennummer von 0 bis 49 und rechts den Spannbaum zu einem ersten Schwellwert $S=91$, dem Mittelwert der Abstände im Spannbaum.
Die Bilder können durch Klick in Originalgröße angezeigt werden.

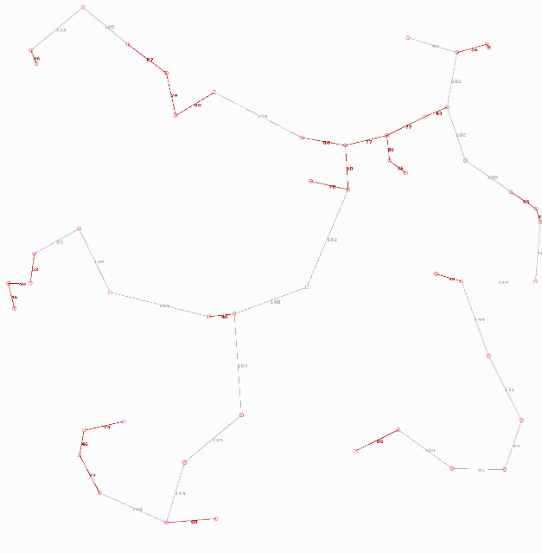
Erhöht man nun den Schwellwert auf $S=130$ werden die Cluster etwas deutlicher. Die Bilder zeigen die Kanten mit Gewicht größergleich S in hellgrau, die clusterbildenden Kanten in rot.
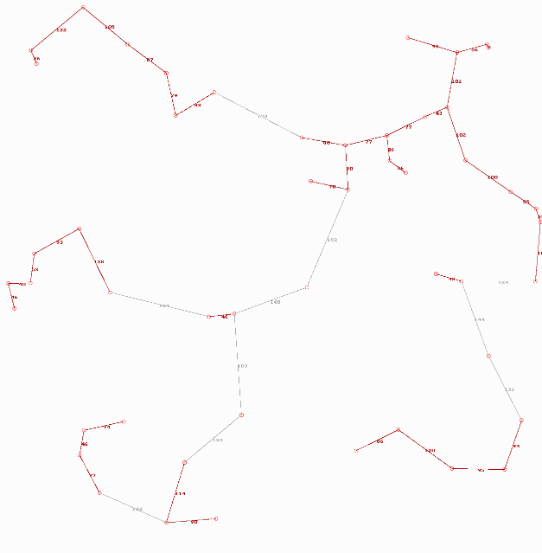
Um das Clustering etwas deutlicher zu machen, habe ich die Möglichkeit eingebaut, "Ballungszentren" einzustreuen (die ebenfalls zufällig positioniert werden), die eine gewisse Anziehungskraft auf die in der Umgebung liegenden Knoten ausüben; so kann man schrittweise stärkere Zusammenballungen erzeugen. In jedem Schritt wird der Abstand eines Knoten zum jeweils nächsten Ballungszentrum um 10 % reduziert. Die Abbildungen zeigen den Anfangszustand, die Ballung nach 4 Schritten und die Auswertung im Spannbaum mit dem Schwellwert $S=121$. Dabei sind die Ballungszentren in den grünen Bildern als kleine blaue Kreise eingezeichnet. Die Bilder zeigen 100 Knoten mit 5 Ballungszentren.


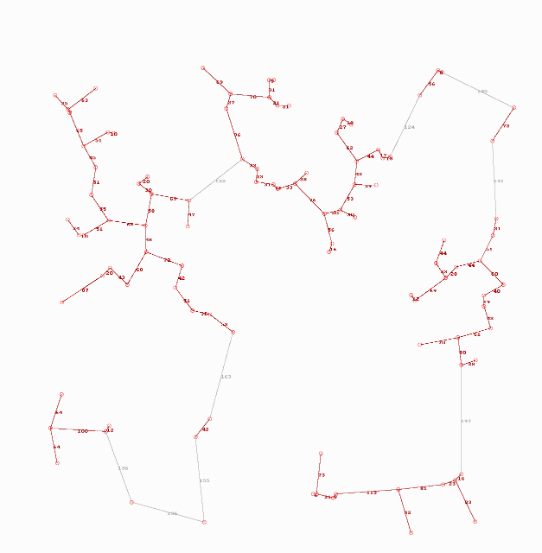
Eine weitere Modifikation stellt die Wahl der Metrik dar. Außer dem bisher benutzten euklidischen Abstand habe ich auch noch die Französische Eisenbahnmetrik und die Manhattanmetrik implementiert.
Die Französische Eisenbahnmetrik ist ein Unikum unter den Metriken; sie bezieht sich auf einen festen Punkt P und misst die Abstände zwischen zwei Punkten A und B immer über P, d.h. der Abstand zwischen A und B ist die Summe der Längen zwischen AP und PB. Formal:
$$
d_P(A,B) := d(A,P) + d(P,B) \text{ für festes P und euklidische Metrik d}
$$
Der Name dieser Metrik stammt aus den Zeiten als das Schienennetz der französischen Eisenbahn fast komplett auf Paris orientiert war, was bedeutete, dass man um von, sagen wir Marseille nach Bordeaux zu fahren, über Paris musste. Tatsächlich ist $d_P$ aber im Sinne der mathematischen Definition eine korrekte Metrik. Was geschieht, wenn wir sie im Clusterprogramm statt der euklidischen verwenden?
Als P habe ich den Mittelpunkt der 1000 x 1000 Einheiten großen Zeichenfläche verwendet, also den Punkt (500, 500). Das Ergebnis ist ebenso überraschend wie einleuchtend. Schauen wir uns die Graphiken an (30 Knoten):

Das Zentrum des Sterngraphs auf der rechten Seite ist der Knoten mit Nummer 4; er liegt dem Punkt P der Eisenbahnmetrik am nächsten, die roten Kanten des minimalen Spannbaumes liegen unterhalb des berechneten Mittelwertes $S=471$. Bei der zweiten Graphik habe ich die Koordinaten von P auf (250, 250) gelegt ...
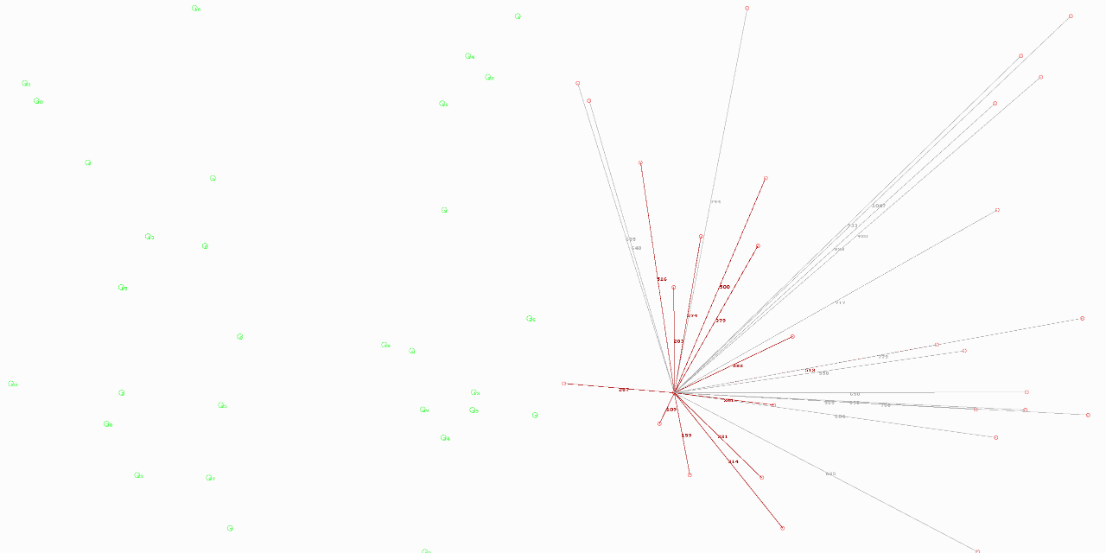
... was das Zentrum auf den nächstliegenden Knoten 2 verschiebt.
Das Pascalprogram zur Clusteranalyse füge ich für eigene Versuche bei.
Clusteranalyse.zip
Die klassische Anwendung von minimalen Spannbäumen ist das flächendeckende, aber möglichst kostengünstige Versorgen von Landstrichen mit leitungsgebundenen Versorgungsgüter, also z.B. Stromleitungen, Glasfaserkabeln, Fernwäre usw. Dabei sind die Versorgungsstellen einerseits und die Versorger andererseits die Knoten, die Leitungen die Kanten und die Kantengewichte sind die Erstellungskosten, die pro Leitung anfallen. Der minimale Spannbaum verbindet nun alle Knoten zu insgesamt minimalen Kosten. Dieses Prinzip wurde zum ersten Male 1926 von Otakar Boruvka in Mähren angewendet, der den Auftrag hatte, ein Konzept für die landesweite Elektrifizierung zu erstellen.
Aber nun zum Algorithmus von Kruskal, mit dem ich die Spannbäume berechnet habe. Auf vielen Seiten im Internet wird der Programmablauf einfach so oder ähnlich beschrieben:
- Sortiere die Kanten des Graphen aufsteigend nach ihrem Gewicht und speichere sie in einer Liste
- Füge, beginnend mit der Kante kleinsten Gewichts, die Kanten in den zu erstellenden Spannbaum ein
- Wenn durch das Einfügen im Spannbaum ein Kreis entstünde, dann lass die Kante weg und versuche es mit der nächstgrößeren
- Setze das Einfügen fort, bis der Spannbaum fertig ist
Diese Beschreibung sieht tatsächlich sehr einfach aus, aber sie hat ihre Tücken; gewiss für das erste Verständnis mag sie ausreichend sein, aber beim Programmieren und Testen erkennt man dann die ganze Wahrheit. Gehen wir die einzelnen Schritte durch.
zu 0. Zunächst muss man den Graphen im Programm bereitstellen, das erfolgt auch hier wieder über die Adjazenzmatrix, die in diesem Fall symmetrisch ist, auf der Diagonale Nullen enthält und sonst die Kantengewichte. Wegen der Symmetrie könnte man das Speichern auf die über der Hauptdiagonale liegende Dreiecksmatrix beschränken - habe ich in meinem Programm nicht gemacht.
zu 1. Das Sortieren kann in einem Array erfolgen (eine lineare Liste ist nicht sinnvoll); wenn man es optimal machen will und vor allem bei größeren Graphen, verwendet man den Quicksort. Ich habe in meinem Programm der Einfachheit halber das Sortieren mit dem Einfügen der Kanten aus der Adjazenzmatrix verbunden. Für die Spezialisten: eine weitere Optimierung kann durch das Sortieren mittels eines Heap-Sorts erfolgen; man sortiert dann nur so weit, wie man die Kanten braucht, also bis der Spannbaum fertig ist.
zu 2. Der Spannbaum wird wiederum durch eine Adjazenzmatrix repräsentiert, wenn man Speicherplatz sparen will, kann man die Kanten auch auf dem Platz der Ausgangsmatrix speichern, man hat die Kanten ja in dem sortierten Array.
zu 3. Dies ist der Knackpunkt der Kurzbeschreibung; es ist zwar richtig, dass keine Kreise im Spannbaum entstehen dürfen, aber die naive Vorgehensweise - Kante einfügen, Prüfen, ob es einen Kreis gibt - wenn ja, Kante wieder rausnehmen - ist nicht das Gelbe vom Ei. (Oft ist im Internet der Pseudocode zum Kruskal noch mit einer animierten Darstellung verbunden, bei der man "sieht", wie beim Einfügen ein Kreis entsteht und das wieder rückgängig gemacht wird.) Denn die Prüfung, ob in einem Graphen ein Kreis enthalten ist, stellt einen eigenen aufwändigen Algorithmus dar (siehe [26]: "Algorithmisch lassen sich Zyklen in einem Graphen durch modifizierte Tiefensuche finden"). Deshalb wird an dieser Stelle ein ganz anderes Verfahren verwendet. Man prüft beim Einfügen einer neuen Kante, ob die Endknoten in unterschiedlichen Zusammenhangskomponenten des (noch unfertigen) Spannbaumes liegen; wenn ja, dann kann die Kante eingefügt werden, sonst geht man zur nächsten Kante über. Man vermeidet dadurch die Kreisbildung in einer Zusammenhangskomponente. Auch diese Prüfung muss programmtechnisch verwaltet und durchprogrammiert werden; das Verfahren, das hier zur Anwendung kommt, heißt in der Informatik "Union-Find" Datenstruktur [27]. Es verwaltet die Knoten der bisher entstandenen Zusammenhangskomponenten als Knotenmengen und vereinigt (Union) zwei solche Mengen, wenn man eine Kante einfügt, deren Endpunkt eben in unterschiedlichen Mengen liegt. Am Anfang des Algo liegen alle Knoten in unterschiedlichen Mengen (also pro Knoten eine eigene Menge), am Ende hat man nur noch eine solche Menge übrig, die alle Knoten enthält, also die Zusammenhangskomponente des Spannbaumes bildet. Die Realisierung kann auf unterschiedliche Weise erfolgen; die Mengen können als Baum oder auch als Array realisiert werden. Ich habe ein Array von Arrays verwendet. Implementierungen als SET im Sinne von Pascal wären zwar programmtechnisch einfacher, scheitern aber an der Obergrenze der Mächtigkeit von SETs in Pascal, die in FPC bei 256 liegt.
zu 4. Auch hier zeigen die Animationen des Verfahrens das Ende oft nach dem Motto "Sieht man doch, Spannbaum ist fertig", aber auch dies muss differenzierter betrachtet werden, denn der Algorithmus kann nicht voraussetzen, dass der eingegebene Graph überhaupt einen Spannbaum hat (siehe Satz 3.4e). Optimaler Weise liefert der Algo eine Aussage, ob der Graph zusammenhängend ist oder nicht. Dass es einen Spannbaum gibt, kann man entweder über die Anzahl der eingefügten Kanten im Vergleich zur Knotenzahl des Graphen feststellen (Satz 3.4c, also $m(Spannbaum)=n(G)-1$) oder prüft, ob das Union-Find-Verfahren genau eine komplette Spannbaummenge erzeugt hat. Dies kann im Extremfall erst mit der letzten Kante passieren. Wenn aber die Menge der Kanten erschöpft ist bevor eine der oben genannten Bedingungen erfüllt ist, dann gibt es keinen Spannbaum, was bedeutet, dass der Ausgangsgraph nicht zusammenhängend ist.
Für das Verfahren von Kruskal habe ich eine eigene Pascal-Unit gebaut, die in verschiedenen Programmen eingesetzt werden kann. Das Programm Spannbaum ruft diese Unit auf und gibt den Spannbaum als Adjazenzmatrix aus. Das Einlesen der Adjazenzmatrix erfolgt aus einer txt-Datei.
Spannbaum.zip4 Panta rei - Alles fließt
4.1 Nichts wie raus!
Definition 4.1 (Flussnetzwerk)
Sei $G=(V,E)$ ein gerichteter Graph, $c:E \rightarrow \mathbb{R}^+_0$ eine Kapazitätsfunktion (entspricht den Gewichten) und $s, t \in V, \; s \neq t$ zwei Knoten, der Quelle $s$ und der Senke $t$. Dann heißt $N = (G, c, s, t)$ ein Flussnetzwerk.
Die Kapazitätsfunktion $c$ beschreibt den maximalen Durchsatz durch eine Kante auf dem Weg vom Startknoten zum Endknoten der Kante. Je größer der Funktionswert desdo größer der mögliche Durchsatz.
In unserem Beispiel sagt der Kapazitätswert einer Kante etwas über die Anzahl der Menschen pro Zeiteinheit aus, die die Kante durchlaufen (in des Wortes doppelter Bedeutung) können. Ziel ist es, möglichst viele Menschen (möglichst schnell) zu evakuieren. Wie kann man sich den Graphen vorstellen? Die Kanten entsprechen den Fluchtwegen, also zum größten Teil die Gänge des Gebäudes. Da Gänge normalerweise in beiden Richtungen begangen werden können, gibt es im Graphen zwei gerichtete Kanten zwischen zwei Knoten, die jede für sich einen Kapazitätswert haben. Die müssen aber nicht gleich sein, wenn man beispielsweise daran denkt, dass auch Treppen begangen werden müssen und die kann man abwärts schneller als aufwärts überwinden. Auch ist es denkbar, dass ein Fluchtweg nur in einer Richtung benutzt werden kann, z.B. wenn ein Teil eines Fluchtweges in einer Notrutsche besteht, die man aufwärts nicht nutzen kann. Die Knoten sind Abzweigungen bzw. Kreuzungen im System der Gänge, aber auch Räume oder besser deren Türen, die als Startpunkte der Flucht gelten. Ein solcher Knoten wird dann die Rolle der Quelle $s$ übernehmen. Die Senke $t$ ist der Sammelpunkt, der das Ziel der Flucht darstellt. Nehmen wir an, unser Gebäude hat folgende Gestalt:
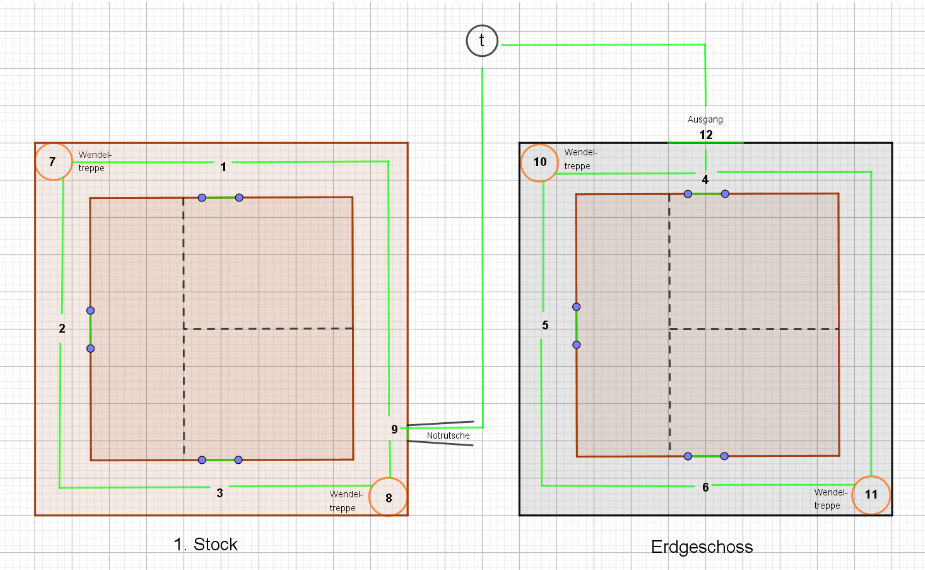
Die Ziffern stellen die Knoten des Graphen dar, 1 bis 6 stehen für die Räume aus denen evakuiert werden sollen, also als mögliche Startknoten. Es gibt zwei Möglichkeiten das Gebäude zu verlassen, den normalen Ausgang im Erdgeschoss (12) oder die Notrutsche (9) im 1. Stock. Die Wendeltreppen können in beiden Richtungen begangen werden, aufwärts aber langsamer als abwärts.
Stellen wir nun ein Flussnetzwerk dazu auf:
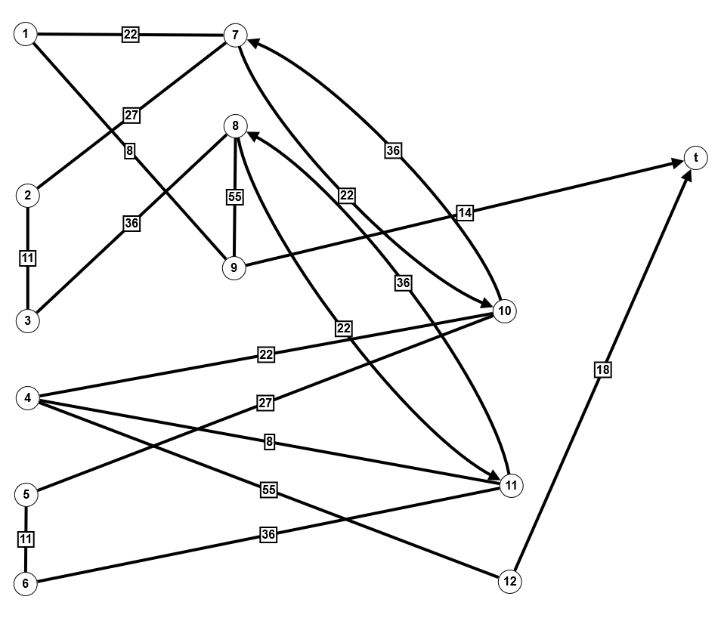

Die Gewichte an den Kanten, also die Kapazitäten, berücksichtigen grob die zurückzulegenden Entfernungen und oben schon genannte "Hindernisse"; sie können als "evakuierbare Personen pro Zeiteinheit" angesehen werden. Die Flucht aus dem Gebäude gilt erst als (gelungen) beendet, wenn der Zielknoten "t" erreicht ist. Als Startknoten können die Räume 1 bis 6 angesehen werden und wir nehmen an, dass nur ein Raum evakuiert werden muss, die anderen also leer sind.
Entwickeln wir nun aber die Mathematik etwas weiter. Um was geht es denn jetzt eigentlich? Das Wort heißt "Fluss" durch das Netzwerk, d.h. der "Transport" von Einheiten vom Startpunkt zum Zielpunkt und das mit möglichst großer Kapazität. Diesen Fluss zu berechnen ist die Aufgabenstellung, aber erst mal müssen wir diesen Begriff mathematisch definieren.
Definition 4.2 (Fluss)
Vorgegeben sei ein Flußnetzwerk $N=(G,c,s,t)$. Bezeichne $E_{in}(v) := \{(u,v) \in E\}$ und $E_{out}(v) := \{(v,u) \in E\}$, also die Menge aller Kanten, die den Knoten $v$ münden, bzw. die $v$ verlassen. Eine Abbildung $f: E \rightarrow \mathbb(R)$ heißt Fluss, wenn gilt:
a) $0 \leq f(e) \leq c(e)$ für alle $e \in E$: die Kapazität keiner Kante wird überschritten.
b) $\sum_{e \in E_{in}(v)} = \sum_{e \in E_{out}(v)}$ für alle $v \in V \setminus \{s,t\}$: es fließt genauso viel aus einem Knoten heraus wie hinein, abgesehen von s und t.
Satz 4.3
Für einen Fluss $f$ gilt: $\Phi(f):= \sum_{e \in E_{out}(s)}f(e) - \sum_{e \in E_{in}(s)} f(e) = \sum_{e \in E_{in}(t)}f(e) - \sum_{e \in E_{out}(t)} f(e). \Phi(f)$ nennt man den Wert des Flusses $f$ auf $N$. Das größte $\Phi(f)$ unter allen $f$ heißt Maximalfluss.
Und den wollen wir finden.
Der Algorithmus zur Berechnung des Maximalflusses wurde von Ford und Fulkerson entwickelt. Der entscheidende Begriff dabei ist der "Zunehmende Weg" auch "Augmentierender Weg" genannt. Ein solcher Weg hat die Eigenschaft, den Wert des Flusses zu erhöhen (augmentieren) und damit dem Maximalfluss näher zu kommen. Wenn man keinen zunehmenden Weg mehr findet, hat man den Maximalfluss.
Definition 4.4 (Zunehmender Weg)
Sei N ein Flussnetzwerk mit einem Fluss $f$.
Eine Folge $(v_0, v_1, \cdots, v_k)$ heißt zunehmender Weg bezgl. f, wenn für jedes $i \in \{1, \cdots, k\}$ eine der folgenden Bedingungen gilt:
a) $(v_{i-1}, v_i) \in E$ und $f((v_{i-1}, v_i)) < c((v_{i-1}, v_i)) $ Vorwärtskante
b) $(v_i, v_{i-1}) \in E$ und $f((v_i, v_{i-1})) > 0$ Rückwärtskante
Ein zunehmender Weg besteht also aus einer Reihung von Knoten des Graphen unabhängig davon, in welcher Richtung eine verbindende Kante zeigt. Die Werte von f auf den Kanten müssen dabei die genannten Bedingungen erfüllen, bei a) im Vergleich zur Kapazität, bei b) gegenüber Null.
Die Bedeutung der zunehmenden Wege unterstreicht der Satz:
Satz 4.5
Ein Fluss $f$ in einem Flussnetzwerk $N$ ist genau dann ein Maximalfluss, wenn es keinen zunehmenden Weg von s nach t gibt.
Wir legen unser Fluchtwegbeispiel einen Moment zur Seite und betrachten zum Verstehen des Ford-Fulkerson ein einfacheres Beispiel.
Auf der Webseite [28] findet man ein sehr schönes Tutorial mit der Möglichkeit den Algo Schritt für Schritt nachzuvollziehen. Die folgenden Abbildungen habe ich dort erstellt.
Als erstes Bild natürlich den Ausgangsgraph mit s und t und den Kapazitäten des Netzes:
 $G$
$G$Die Dicke der grauen Unterlegungen der Kanten geben einen Eindruck von der Größe der Kapazität der Kante. Zu Beginn des Algo geht man von einem Fluss von Null auf allen Kanten aus, den wir $f_1$ nennen wollen. Der momentane Flusswert wird vor die Kantenkapazität geschrieben, hier wie gesagt 0.
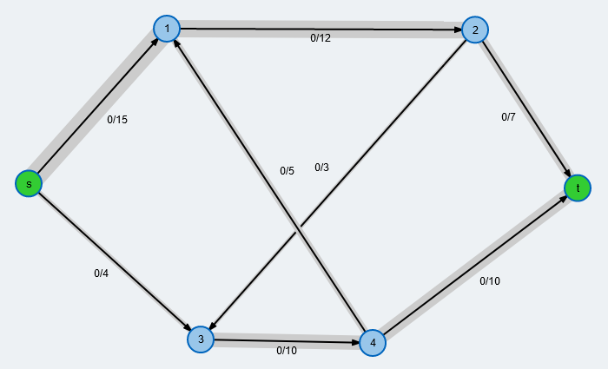 $f_1$
$f_1$Als Hilfsmittel zum Auffinden eines zunehmenden Weges von s nach t bildet man den sog. Reste- oder Residualgraph. Er stellt die noch freien Kapazitäten, besser die Möglichkeiten zur Vergrößerung des Flusses vom aktuell berechneten Fluss zur Maximalkapazität der Kanten dar:
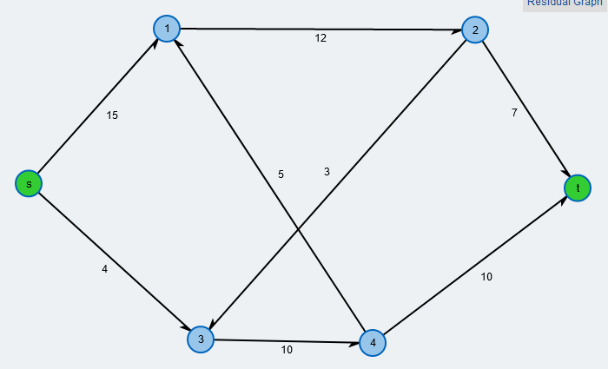 $G_{f_1}$
$G_{f_1}$Diese Reste bestehen im ersten Schritt natürlich aus den Kapazitäten der Kanten. Jetzt kommt der entscheidende Schritt, die Suche eines zunehmenden Weges. Wenn es mehrere gibt, dann ist es letztlich egal, welchen man nimmt (eine Weiterentwicklung des Ford-Fulkerson sucht dort immer den kürzesten Weg). Wir wählen hier s - 3 - 4 - t.
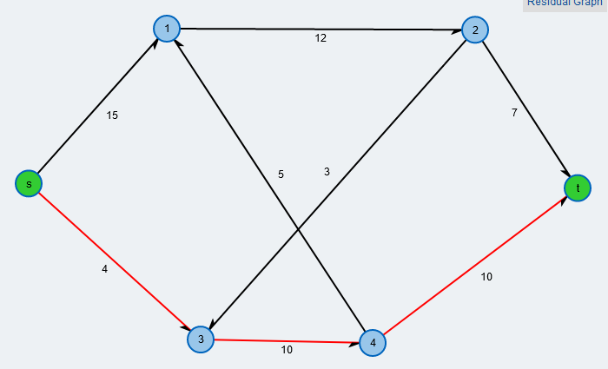
Man muss natürlich prüfen, ob dieser Weg tatsächlich die Definition 4.4 erfüllt. Die drei beteiligten Kanten sind Vorwärtskanten, also muss Bedingung a) gelten. Der Fluss $f_1$ auf diesen Kanten ist aber überall Null, so ist die Bedingung erfüllt. Netterweise gilt der Satz:
Satz 4.6
Jeder Weg von s nach t im Residualgraphen ist ein zunehmender Weg.
Entlang des zunehmenden Weges erhöht man nun den Fluss $f_1$ bis zur Kapazitätsgrenze der Kanten mit der geringsten Kapazität (hier die Kante s - 3). Also erhalten wir einen neuen Ausgangsgraphen mit Fluss $f_2$:
 $f_2$
$f_2$Nun beginnt ein neuer Augmentierungsdurchlauf, wieder mit der Bildung des Residualgraphen:
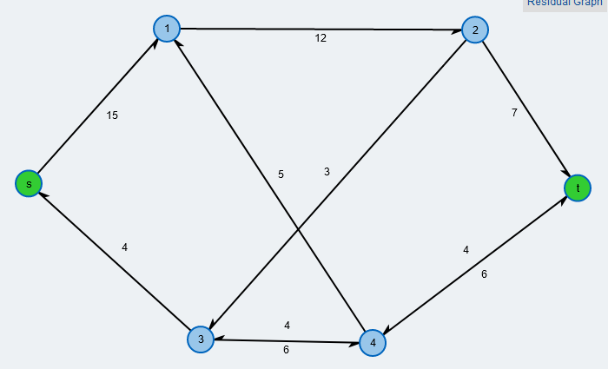 $G_{f_2}$
$G_{f_2}$Um hier gleich einem Missverständnis vorzubeugen: eine Kante, deren Fluss in einem vorherigen Schritt vergrößert wurde, kann in einem weiteren Schritt auch wieder verkleinert werden, wenn das dem Gesamtziele eines maximalen Flusses durch das Netz dienlich ist. Deshalb findet man in dem neuen Residualgraphen bei den Kanten 3 - 4 und 4 - 6 zwei Einträge: in der ursprünglichen Richtung $3 \rightarrow 4$ eine 6 für Restkapazität in dieser Richtung und $4 = 10 - 6$ für die Gegenrichtung; dieser Wert kann für eine Verkleinerung verwendet werden.
Regel 4.7 [29]
Im Residualgraph $G_f$ zu einem Fluss wird gespeichert, um welchen Wert der Fluss jeder Kante noch verändert werden darf:
a) Hat eine Kante $(v,w)$ den Fluss $f(v,w) > 0$, dann darf der Fluss verkleinert werden. Im Residualgraph wird die Kante $(w,v)$ mit dem Residualfluss $f((v,w))$ abgespeichert. Diese Kante im Residualgraph verläuft in umgekehrter Richtung (Flusserhöhung in umgekehrter Richtung verkleinert den Fluss).
b) Hat eine Kante $(v,w)$ den Fluss $f((v,w)) < c((v,w))$, dann darf der Fluss vergrößert werden. Im Residualgraphen wird die Kante $(v,w)$ mit dem Residualfluss $c((v,w)) - f((v,w))$ abgespeichert.
Nach dieser Regel spart man sich im Falle von f((v,w)) = 0 das Eintragen des Flusswertes (überall im ersten Residualgraphen).
Als zunehmender Weg wird s - 1 - 2 - t gewählt.
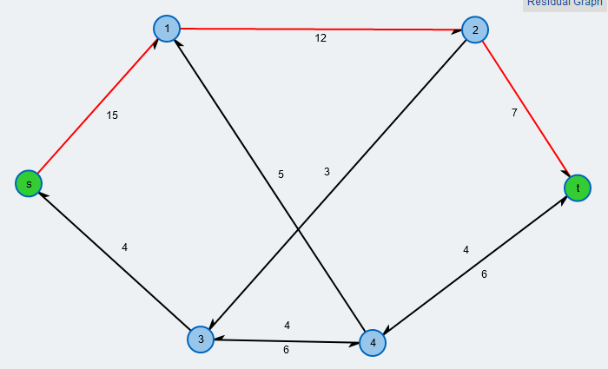
Das führt zum Fluss $f_3$, bestimmt durch die Kante $(2,t)$.
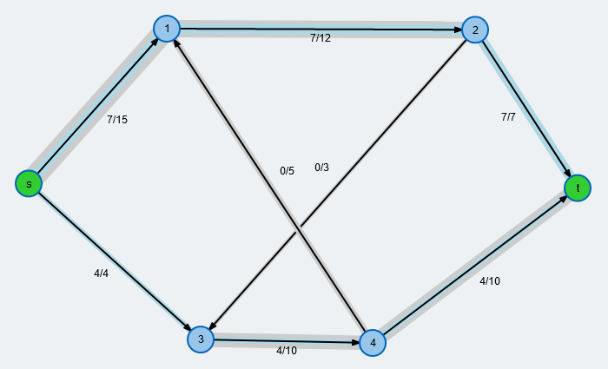 $f_3$
$f_3$Der bisherige Flusswert liegt $7 + 4 = 11$. Kommt noch mehr? Also wieder Residualgraph:
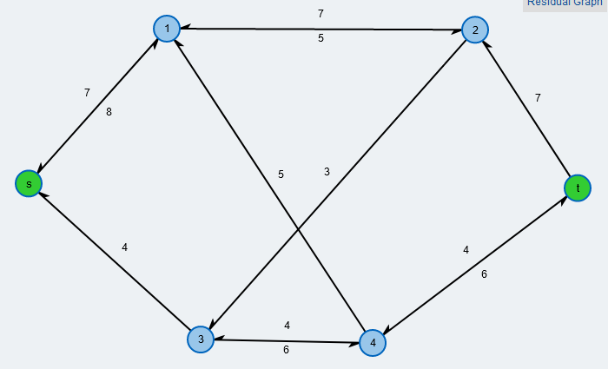 $G_{f_3}$
$G_{f_3}$Wie findet man jetzt den geeigneten zunehmenden Weg. Startend bei s ist es nicht sinnvoll in Richtung 3 zu gehen, denn da hat man ja keine Flußerhöhung, also Richtung 1; mit gleichem Argument sind 2 und 3 die nächsten Knoten. Zurück nach s wäre ziemlich unsinnig, also weiter nach 4 und dann nach t.
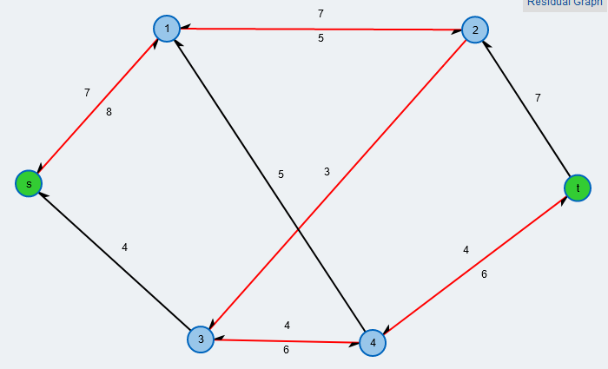
Die Kante mit der kleinsten Restkapzität ist $(2,3)$. Somit haben wir:
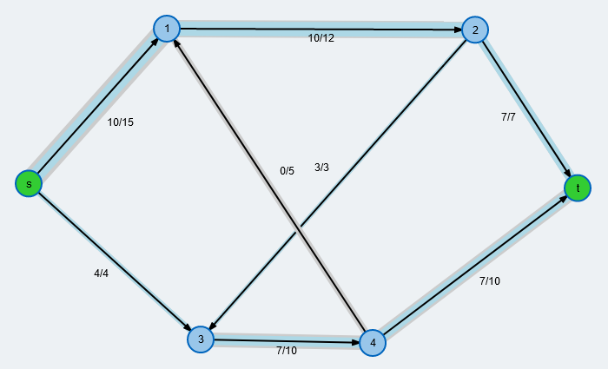 $f_4$
$f_4$Na, schaffen wir noch was? Residualgraph:
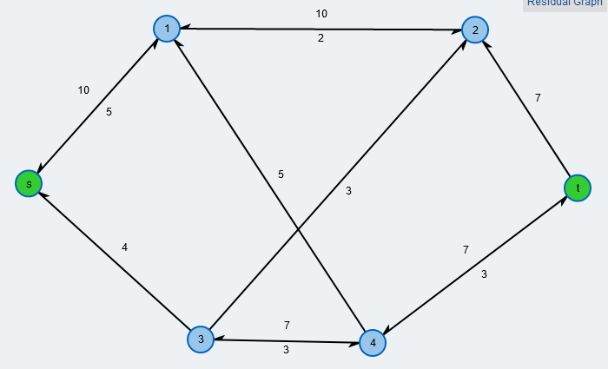 $G_{f_4}$
$G_{f_4}$Nach 4 können wir von s aus wieder nicht gehen, aber nach 1 und von da nach 2 geht noch. Aber dann ist Ende Gelände. Kein zunehmender Weg mehr in Sicht. Das führt zum Endergebnis:
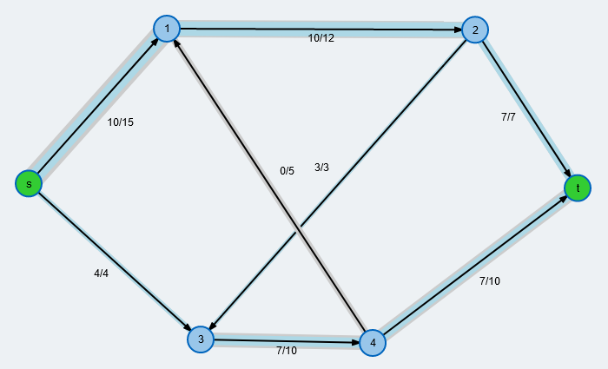 $f_5$
$f_5$Der Wert $\Phi(f_5)$ des maximalen Flusses ergibt sich durch Summation der von s "weglaufenden" Flüsse oder gleich dem der Summe der auf t "zulaufenden" Flüsse, also zu 14.
So, nachdem wir jetzt wissen, wie Ford-Fulkerson läuft, können wir ihn auf unsere Fluchtwegeoptimierung loslassen. Ich benutze dafür eine Realisierung, die in [30] angeboten wird. Sie stellt die Ergebnisflüsse durch mehr oder weniger dicke Pfeile dar, sodass man schnell sieht, wo sich die Hauptströme bewegen.
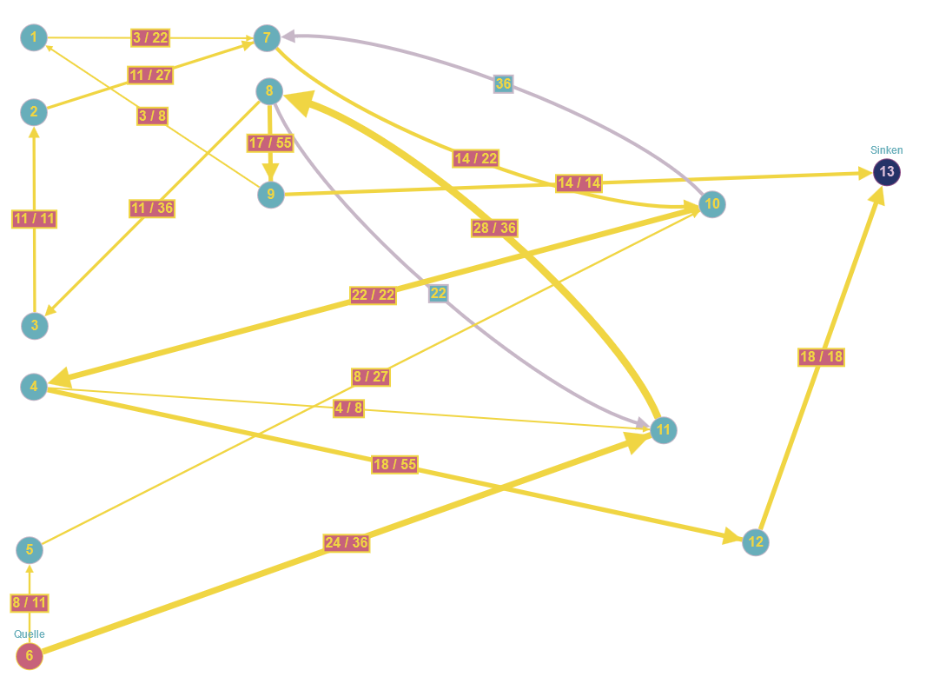

Als Quelle wurde Raum 6 gewählt. Zur Erinnerung, 12 ist der normale Ausgang, 9 die Rutsche aus dem 1. Stock. Aufgrund der etwas geringeren Kapazität der Rutsche kommen hier nur 14 Personen pro Zeiteinheit im Gegensatz zu 18 über den normalen Ausgang. Außerdem sieht man, dass der sich vor der Rutsche 9 bildende Andrang von 17 Personen in zwei Ströme aufteilt (3 und 14), wobei die 3 Personen sich über die Wendeltreppe bei 7 zum Ausgang 12 durchschlagen. Die Gänge mit dem größten Durchsatz sind der von 11 nach 8, also die Wendeltreppe nach oben(!) und von 6 nach 11. Der maximale Fluss von 6 nach t ist 32.
Nehmen wir nun an, dass zwischen Zimmer 6 und der Wendeltreppe 11 aufgrund eines Ereignisses kein Durchkommen mehr ist (verschüttet, verraucht, etc.). Ein erneutes Berechnen des maximalen Flusses ergibt nur noch 11, das ist letztlich die Kapazität des Weges von 6 nach 5. Die 11 verteilen sich zu 3 auf den Ausgang und zu 8 auf die Rutsche.
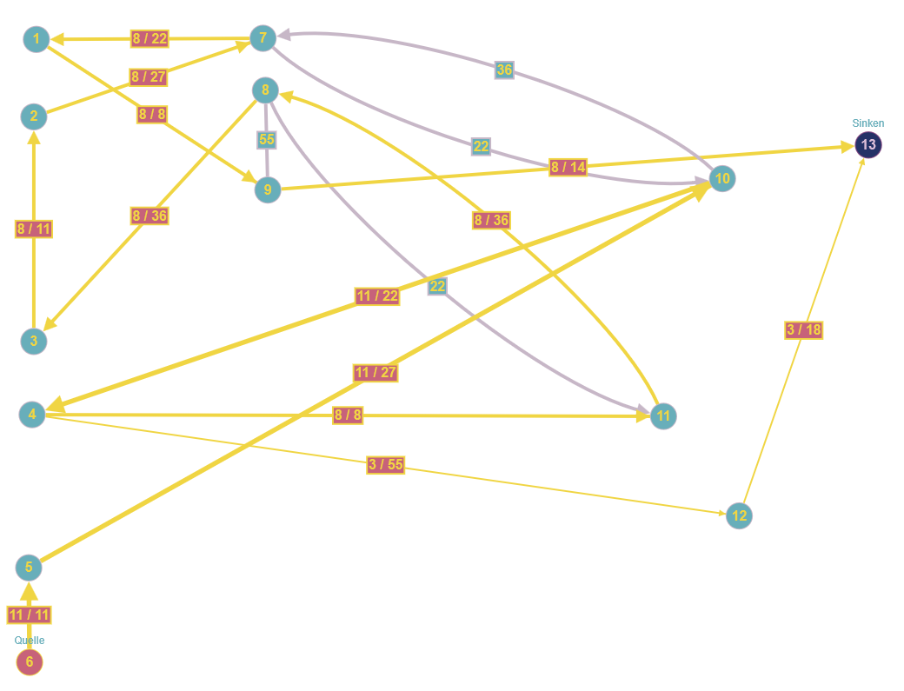
Ein weiterer Begriff im Zusammenhang mit Flussnetzwerken ist der des Schnittes; hier kann man sich Schnitt tatsächlich als Schere vorstellen, wenn die Kanten des Graphen als Bindfäden realisiert wären. Im nächsten Graphen sieht man die Bedeutung eines Schnittes als limitierendes Element in einem Flussnetzwerk:
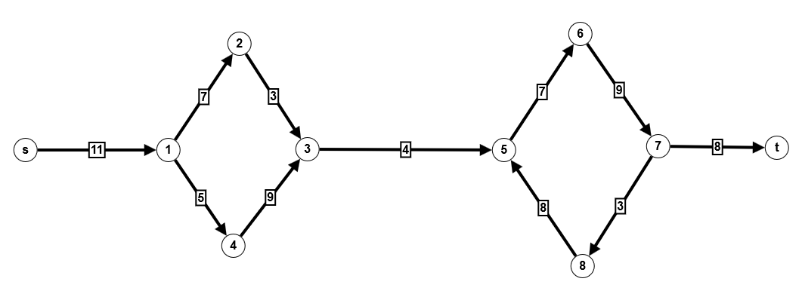
Die Kante $(3,5)$ hat die Kapazität 4; kein Fluss von s nach t kann größer sein als 4, denn der Fluss muss durch dieses Nadelöhr. Die Kante $(3,5)$ repräsentiert den Schnitt. Schneidet man die Kante tatsächlich durch, läuft nichts mehr.
Definieren wir nun:
Definition 4.8
Sei $N=(G,c,s,t)$ ein Flussnetzwerk mit $G=(V,E)$. Seien $S, T \subset V$ mit $S \cup T = V, \; S \cap T = \{\}, \; s \in S, \; t \in T$. (Also ist $T = V \setminus S$). Dann heißt $C_S := \{(v,w) \in E | v \in S, \; w \in T\}$ ein Schnitt. Ist $c(C_S) := \sum_{c \in C_S} c(e)$, die Kapazität des Schnittes, minimal, dann handelt es sich um einen minimalen Schnitt.
In obigem Beispiel ist $S=\{s, 1, 2, 3, 4\}, \; T = \{5, 6, 7, 8, t\} $ und $ C_S = \{(3,5)\}$, weiterhin $c(C_S) = 4$, was genau dem maximalen Fluss entspricht. Das ist kein Zufall, denn es gilt der Satz:
Satz 4.9 (Max-Flow-Min-Cut-Theorem)
In einem Flussnetzwerk ist der Wert eines maximalen Flusses gleich der Kapazität eines minimalen Schnittes.
Bemerkung 4.10
Beim Fluss betrachtet man das, was tatsächlich durch die Kanten fließt, beim Schnitt aber die Ausgangskapazitäten der Kanten.
Wie findet man nun einen minimalen Schnitt in einem Flussnetzwerk? [31] Auch hier spielt der Residualgraph eine hilfreiche Rolle. Man benutzt den Residualgraph der zum maximalen Fluss gehört; dies ist in unserem Beispiel zur Anwendung des Ford-Fulkerson der Residualgraph $G_{f_4}$.
 $G_{f_4}$
$G_{f_4}$1. Schritt (S und T bilden)
Regel: Für jeden Knoten $v \in V$: Wenn der Weg von s nach v in $G_f$ existiert, dann füge v in S ein, sonst in T. Damit ist auch $s \in S$ und $t \in T$.
Im Beispiel: $ S = \{s, 1, 2\}, \; T = \{3, 4, t\}$
2. Schritt ($C_S$ bilden)
Regel: Für jede Kante $e \in E$: Wenn der Startknoten von e zu S gehört und der Endknoten zu T, dann füge e in $C_S$ ein.
Im Beispiel: $C_S = \{(s,3), (2,3), (2,t)\}$. $(4,1)$ gehört nicht dazu, da falsche Richtung!
Stellen wir nun den Schnitt durch die 3 Kanten optisch dar:
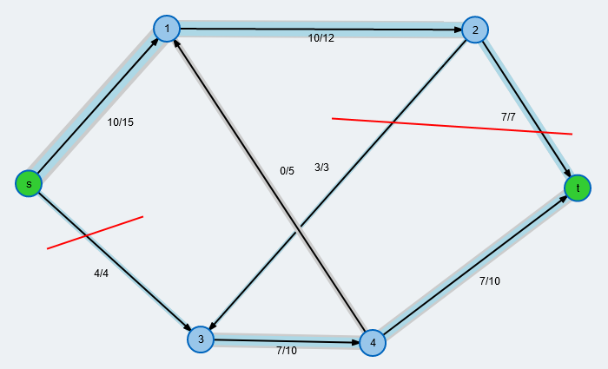
Die Kapazität des Schnittes berechnet sich zu $c((s,3)) + c((2,3)) + c((2,t)) = 4 + 3 + 7 = 14$. Dies stimmt natürlich mit dem maximalen Fluss überein. Auch hier fließt nichts mehr von s nach t, wenn man den Schnitt in der Realität durchführt.
4.2 Wer mit wem?
Wir haben, sagen wir 5 Männer und 5 Frauen, die sich untereinander teilweise kennen. Wir stellen sie und die Beziehung "M kennt F" in einem bipartiten Graphen dar:
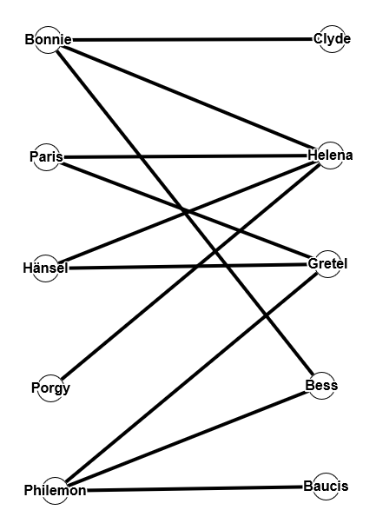

Wir suchen nun ein Matching im Sinne von "M heiratet F" für möglichst viele Paare mit der Nebenbedingung, dass sie sich kennen müssen (es also eine Kante zwischen ihnen gibt). Heiraten impliziert außerdem, dass es eine Paarbildung ist, Dreierbeziehungen und größere sind nicht erlaubt. Die Knotenmenge der Männer nennen wir S, die der Frauen T.
Definition 4.11 (Matching in bipartiten Graphen)
Sei $G=(V,E)$ ein bipartiter Graph.
a) Eine Menge von Kanten $M \subset E$ heißt Matching (oder Zuordnung), wenn gilt: Für alle $e_1 \neq e_2 \in M:\quad e_1 \cap e_2 = \{\}$. Einfach gesagt, je zwei Kanten haben keinen gemeinsamen Knoten.
b) Ein Matching heißt maximal (oder nicht erweiterbar), wenn durch Hinzunehmen einer weiteren Kante zu $M$ kein (neues) Matching entsteht.
c) Ein Matching heißt perfekt, wenn $2\cdot |M| = |V|$, also wenn jeder Knoten am Matching beteiligt ist.
Ein perfektes Matching ist maximal.
Ziel ist es nun, in einem bipartiten Graphen ein maximales Matching zu finden. Als ich vor einigen Jahren in einer Vorlesung über "Effiziente Algorithmen" hörte, wie das geht, war ich doch einigermaßen überrascht. Denn dass zwischen Flüssen und Matching ein direkter Zusammenhang besteht, schien mir auf den ersten Blick nicht so klar. Aber tatsächlich, wenn es richtig fließt, dann matcht es auch. Man muss den bipartiten Ausgangsgraphen nur richtig aufbereiten, um einen maximalen Fluss berechnen zu können und das machen wir jetzt:
Rezept 4.13
1. Schritt
Aus dem ungerichteten Graphen wird ein gerichteter, indem alle Kanten von S nach T gerichtet werden.
2. Schritt
Ein neuer Knoten s wird mit zugehörigen Kanten $(s,v), v \in S$ hinzugefügt.
3. Schritt
Ein neuer Knoten t wird mit zugehörigen Kanten $(v,t), v \in T$ hinzugefügt.
4. Schritt
Alle Kanten bekommen die Kapazität 1.
Dann sieht das fertige Flussnetzwerk so aus:


Jetzt kann man den Ford-Fulkerson darauf loslassen und erhalten ...
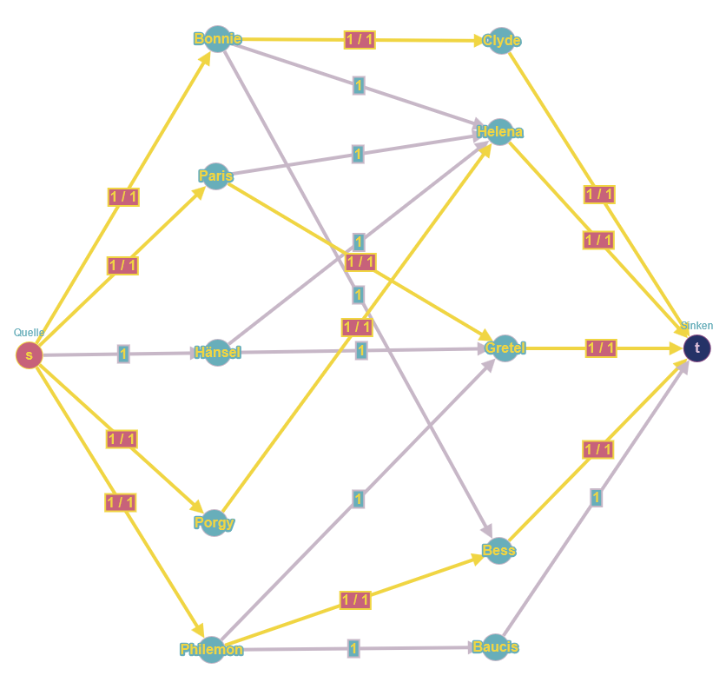
... ein maximales Matching, das aus den Kanten besteht, die den Fluss 1 haben, also in diesem Beispiel Bonnie & Clyde, Paris & Gretel, Porgy & Helena und Philemon & Bess. Für Hänsel und Baucis gibt es bei dieser Lösung keine Partner.
Fassen wir zusammen, was man tun muss, um zu einer Lösung der Matchingaufgabe zu kommen.
Rezept 4.13
a) Bipartiten Graphen in ein Flussnetzwerk umwandeln (gemäss Rezept 4.12)
b) Maximalen Fluss berechnen, z.B. mit dem Algorithmus von Ford und Fulkerson
c) Die Kanten zwischen S und T mit Fluss 1 stellen dann das maximale Matching dar.
Es gibt auch einen Satz, der klärt, wann es ein perfektes (und somit maximales) Matching gibt, der Satz von Hall oder auch Heiratssatz.
Satz 4.14 (Heiratssatz)
Sei $G=(S \cup T, E)$ ein bipartiter Graph.
Es gibt genau dann ein Matching in dem jeder Knoten von S vorkommt, wenn für alle Teilmengen $A \subset S$ gilt: $|N(A)| \geq |A|$. Dabei ist $N(A)$ die Menge der Nachbarknoten von $A$, die immer ganz in $T$ liegt, da $G$ bipartit ist. Gilt darüber hinaus $|S| = |T|$, so ist $G$ perfekt.
Da unser obiger Heiratsgraph nicht perfekt ist, muss es eine Teilmenge von $S$ geben, die weniger Nachbarn als Elemente hat; dies ist der Fall. Man betrachte $\{Paris, Hänsel, Porgy\}$, eine dreielementige Menge; sie hat die Nachbarn $\{Helena, Gretel\}$ und das sind nur 2.
5 Und sonst?
5.1 Wahr - scheinlich
Definition und Satz 5.1
$\Omega$ - Ergebnisraum, also die Menge aller möglicher Ausgänge eines Zufallsexperimentes
$\mathfrak{P}(\Omega)$ - Ereignisraum
$\omega \in \Omega$ - Ergebnis
$A \subset \Omega$ - Ereignis
$P(A) \in [0,1]$ - Wahrscheinlichkeit eines Ereignisses
Seien $A_i \subset \Omega$ paarweise disjunkte Ereignisse. Dann gilt: $P(\dot{\cup}_{i=1..n}A_i) = \sum_{i=1..n}P(A_i)$
$P(A|B) := \frac{P(A \cap B)}{P(B)}$ - Bedingte Wahrscheinlichkeit: Wahrscheinlichkeit, dass A eintritt, wenn B bereits eingetreten ist.
Es gelten folgende Regeln:
$P(\Omega) = 1, P(\{\}) = 0$
$P(\Omega \setminus A) = 1 - P(\Omega)$
$P(A \cup B) = P(A) + P(B) - P(A \cap B)$
$P(A \cap B) = P(A) \cdot P(B)$, wenn A und B unabhängig voneinander sind
$P(A|B)=\frac{P(B|A) \cdot P(A)}{P(B)}$ - Satz von Bayes
Laplace-Experiment
Sei $|\Omega| = n$. Dann ist die Wahrscheinlichkeit eines Elementarereignisses $P(\{\omega\}) = \frac{1}{n}$.
Darstellung eines Zufallsexperimentes mit einem Baum
Um die Wahrscheinlichkeiten eines Zufallsexperimentes darstellen zu können, beginnt man die Zeichnung eines Baumes bei der Wurzel und zeichnet pro Elementarereignis eine Kante mit der Wahrscheinlichkeit dieses Ereignisses.
Kleines Beispiel für einen Münzwurf (Laplace-Experiment), $\Omega=\{\text{Kopf}, \text{Zahl}\}, \; P(\text{Kopf}) = P(\text{Zahl}) = \frac{1}{2}$.
Der Baum wächst mit der Häufigkeit des Münzwurfes; die Blätter des Baumes erhalten die Wahrscheinlichkeiten der jeweiligen (gemischten) Ausgänge und berechnen sich aus den Produkten der Kantenwahrscheinlichkeiten, die von der Wurzel zu diesem Blatt führen.
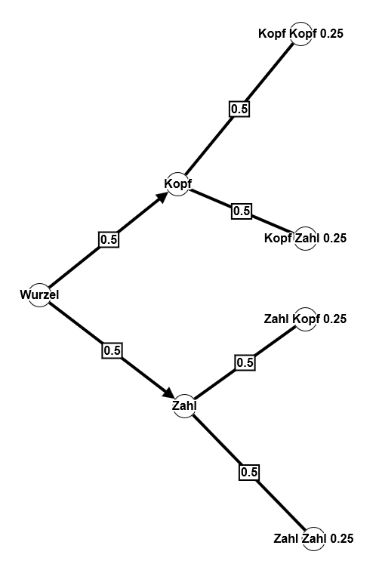
Wie interpretiert man nun das Ergebnis? Nehmen wir an die Fragestellung lautet: Wie groß ist die Wahrscheinlichkeit, bei zweimaligem Werfen einer Münze, zwei unterschiedliche Wurfergebnisse zu erhalten?
Die Frage ist mit Absicht etwas verklausuliert gestellt, ich habe nicht einfach gesagt "... Kopf und Zahl zu erhalten?" um keine Reihenfolge in der Aufgabenstellung zu suggerieren. Mir anderen Worten, die beiden Blätter "Kopf Zahl" und "Zahl Kopf" bilden das Ereignis, dessen Wahrscheinlichkeit wir suchen, also $A:=\{\text{Kopf Zahl, Zahl Kopf}\}$. Hier müssen die beiden Wahrscheinlichkeiten addiert werden um zur Gesamtwahrscheinlichkeit zu kommen, also $P(A) = P( \{\text{Kopf Zahl}\}) + P(\{\text{Zahl Kopf}\}) = 0.25 + 0.25 = 0.5$.
Folgende kleine Aufgabe hat mal vor vielen Jahren ein ehemaliger Kollege von mir in einer Matheklausur gestellt:
Ein Mathematiker zieht morgens ohne hinzusehen zwei Socken aus einer Schublade, die er anziehen will. Wie groß ist die Wahrscheinlichkeit zwei gleicher Farbe herauszuziehen, wenn 4 rote, 2 grüne und 4 blaue Socken in der Schublade liegen?
Auch hier liegt die Lösung mit Hilfe eines Baumes nahe. Man beachte beim Berechnen der Einzelwahrscheinlichkeiten, dass beim Ziehen des zweiten Socken eben ein Socken weniger in der Schublade liegt. Es handelt sich auch hier um ein Laplace-Experiment (genauer um zwei), aber, wie gesagt, ändert sich $|\Omega|$ bei der zweiten Ziehung.
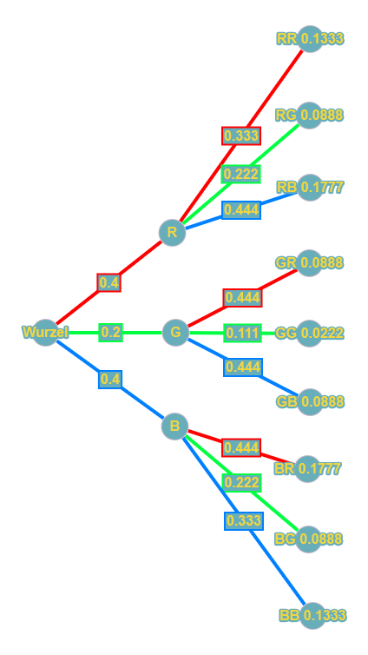
So, jetzt kennen wir die Wahrscheinlichkeiten der 9 Elementarereignisse; wir suchen die Wahrscheinlichkeit des Ereignisses $S=\{RR, GG, BB\}$. Dazu müssen wir noch die Einzelwahrscheinlichkeiten addieren: $P(S) = 0.1333 + 0.0222 + 0.1333 = 0.2888$.
Folgendes Skript vertieft die Informationen zu stochastischer Unabhängigkeit und Wahrscheinlichkeitsbäumen.
Unabhaengigkeit.pdf
Zufallsgraphen
Die zweite Anwendung verbindet nun die Wahrscheinlichkeitsrechnung und Graphen in direkter Weise, genauer, Wahrscheinlichkeiten haben auf das Aussehen von Graphen Einfluss.
Folgendes sehr einfache Beispiel zeigt, was ich meine:
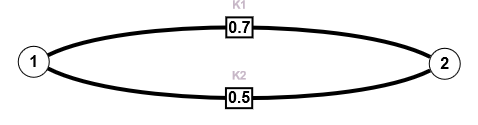
Zwei Knoten sind durch zwei Kanten verbunden, deren Existenz allerdings nicht vollständig gesichert ist. Jede Kante hat eine Wahrscheinlichkeit als Gewicht, die aussagt, wie "durchlässig" die Kante ist. Anders ausgedrückt, ein Signal, das bei Knoten 1 abgeschickt wird, kommt mit einer Wahrscheinlichkeit $p_1=0.7$ bei Knoten 2 an, entsprechend für Kante 2 mit $p_2=0.5$.
Die Frage lautet nun, mit welcher Wahrscheinlichkeit $p_{12}$ kommt ein Signal, das bei 1 durch beide Kanten geschickt wird, bei 2 tatsächlich an.
Zur Lösung dieser Frage greifen wir auf die Methodik des Zufallsbaumes zurück. Die Ereignisse K1 und K2 des einstufigen Experimentes werden kombiniert und liefern durch Multiplikation eine Wahrscheinlichkeit für die Durchlässigkeit von K1 und K2, entsprechend für die Gegenereignisse.
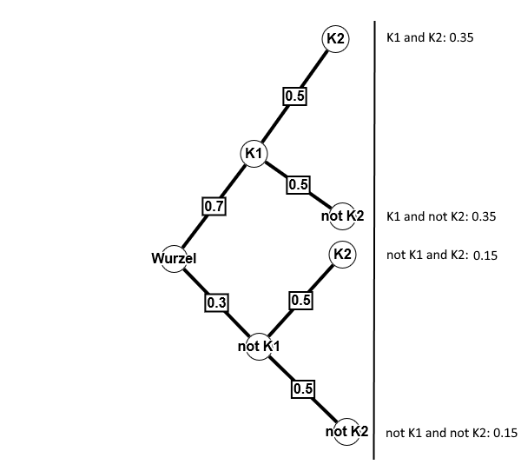
Die Wahrscheinlichkeit dass ein Signal von 1 nach 2 durchkommt, setzt sich nun additiv aus den 3 Wahrscheinlichkeiten zusammen, dass überhaupt etwas durchkommt: P(Signal kommt von 1 nach 2 durch) = 0.35 + 0.35 + 0.15 = 0.85.
Auch hier sieht man, dass bei der Berechnung der Wahrscheinlichkeit P die Betrachtung der Gegenwahrscheinlichkeit schneller zu Ziel führen kann: Die Wahrscheinlichkeit, dass das Signal nicht durchkommt, ist 1 - P = Wahrscheinlichkeit, dass es bei K1 nicht durchkommt und bei K2 nicht durchkommt = 0.3 * 0.5 = 0.15, also P = 0.85.
Ein formales Verfahren, solche Aufgabenstellungen zu lösen, wird in [44] beschrieben und ich will es hier kurz, anhand dieses Beispiels, skizzieren.
Die beiden Ereignisse der Durchlässigkeit von K1 und K2, kann man als logische Aussagen auffassen:
$x1$ := "K1 ist durchlässig" und $x2$ := "K2 ist durchlässig". Das logische Oder verknüpft diese beiden Aussagen zum gewünschten Ziel:
$X:=x1 \vee x2 =$ "K1 ist durchlässig oder K2 ist durchlässig (oder beide)". Eine Umsetzung des logischen Ausdrucks in eine Wahrscheinlichkeitsberechnung gelingt aus naheliegenden Gründen nicht direkt ($p(x1) + p(x2)$ ist natürlich falsch). Vielmehr muss der logische Ausdruck zunächst in eine sog. orthogonale disjunktive Normalform umgeformt werden. Eine disjunktive Normalform (DNF) hat die Form einer Oder-Verknüpfung mehrerer Ausdrücke: $\bigvee_{i=1}^n X_i$, wobei die $X_i$ beliebige logische Ausdrücke sind. Diese Form hat $X$ bereits. Was bedeutet nun orthogonal? Der Ausdruck ist orthogonal, wenn die beteiligten $X_i$ paarweise unverträglich sind, also
$\forall i,j: \, X_i \wedge X_j = false$. Dies gilt in unserem Beispiel allerdings nicht. Wie findet man nun eine orthogonal DNF? Nun, zu jedem Boolschen Ausdruck mit den Variablen $x_k,\, k=1..n$ gibt es eine sog. kanonische DNF und die ist eindeutig (bis auf Reihenfolge der Faktoren) und orthogonal.
Eine kanonische DNF ist eine orthogonale DNF, bei der in jedem Ausdruck $X_i$ alle Variablen $x_k$, evtl. verneint, vorkommen. Um diese kanonische DNF zu bestimmen, gibt es ein Verfahren, das ich im Anhang beschreibe. Hier verrate ich einfach die kanonische DNF des Ausdrucks X:
$X = (x_1 \wedge x_2) \vee (x_1 \wedge \neg x_2) \vee (\neg x_1 \wedge x_2) $.
Natürlich ist die kanonische DNF logisch äquivalent zum Ausgangsausdruck, wie man durch Nachrechen verifiziert. Auch sieht man leicht, dass die Ausdrücke, die durch $\vee$ verbunden sind paarweise unverträglich sind, am Beispiel:
$(x_1 \wedge x_2) \wedge (x_1 \wedge \neg x_2) = (x_1 \wedge (x_1 \wedge \neg x_2) \wedge (x_2 \wedge x_1) \wedge \underbrace{(x_2 \wedge \neg x_2)}_{false}) = false$
Nun ahnt man schon, wie es weitergeht. In $X$ ersetzt man nun $x_i$ durch $p(x_i), \, \neg x_i$ durch $(1-p(x_i)), \, \wedge$ durch mal und $\vee$ durch plus.
$p(X) = (p(x_1) \cdot p(x_2)) + (p(x_1) \cdot (1-p(x_2)) + ((1-p(x_1)) \cdot p(x_2)) = (0.7 \cdot 0.5) + (0.7 \cdot 0.5) + (0.3 \cdot 0.5) = 0.85$
Der folgende Anhang stellt etwas Mathematik zusammen, die obiges Verfahren untermauern und weiter erläutern soll.
Zufallsgraphen.pdf
Zum Abschluss diese Abschnittes noch ein etwas umfangreicheres Beispiel, ebenfalls zum Thema Wahrscheinlichkeit von Durchlässigkeit in Zufallsgraphen. Die Netze, die wir betrachten wollen sind vollständige Graph $ K_2$ bis $K_5$. Die Knoten nummerieren wir gemäß folgender Abbildung für $K_5$ mit 1 bis 5, die Kanten nennen wir dementsprechend $K_{ij}$ für eine Kante vom Knoten $i$ nach $j$; es ist $K_{ij} = K_{ji}$.
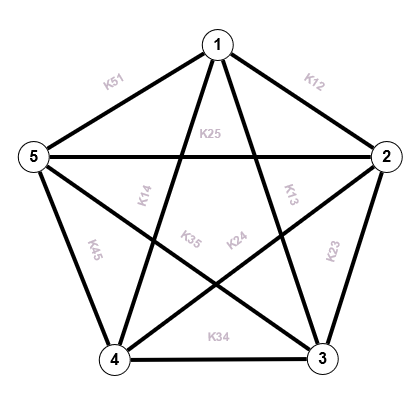
Der Satz 2.6a sagt etwas über die Anzahl der Pfade der Länge k von einem Knoten zu einem anderen Knoten aus. Eine kleine Tabelle stellt die Zahlen zusammen:
$$
\begin{array}{c|c||c|c||c|c||c|c}
\text{n=5}&&\text{n=4}&&\text{n=3}&&\text{n=2}& \\ \hline
\text{Länge k} & \text{Anzahl Pfade} & \text{Länge k} & \text{Anzahl Pfade} & \text{Länge k} & \text{Anzahl Pfade} & \text{Länge k} & \text{Anzahl Pfade}\\ \hline \hline
1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ \hline
2 & 3 & 2 & x & 2 & 1 & \geq 2 & 0 \\ \hline
3 & 6 & 3 & x & \geq 3 & 0 \\ \hline
4 & 6 & \geq 4 & 0 \\ \hline
\geq 5 & 0 \\ \hline
\end{array}
$$
Die Tabelle dient zur Kontrolle der Anzahl der Konjunktionen, die mit or verknüpft einen logischen Ausdruck $f$ zur Beschreibung der möglichen Pfade von Knoten i nach Knoten j bilden. Wir stellen beispielhaft für $K_5$ zusammen:
Die Wahrscheinlichkeit P, dass ein Signal von $1$ nach $3$ durchkommt, ist gegeben durch die Wahrscheinlichkeit, dass
(1) Kante $K_{13}$ intakt ist oder
(2) Kanten $K_{12}$ und $K_{23}$ intakt sind oder
(3) Kanten $K_{14}$ und $K_{34}$ intakt sind oder
(4) Kanten $K_{15}$ und $K_{35}$ intakt sind oder
(5) Kanten $K_{12}$ und $K_{25}$ und $K_{35}$ intakt sind oder
(6) Kanten $K_{12}$ und $K_{24}$ und $K_{34}$ intakt sind oder
(7) Kanten $K_{15}$ und $K_{45}$ und $K_{34}$ intakt sind oder
(8) Kanten $K_{15}$ und $K_{25}$ und $K_{23}$ intakt sind oder
(9) Kanten $K_{14}$ und $K_{24}$ und $K_{23}$ intakt sind oder
(10) Kanten $K_{14}$ und $K_{45}$ und $K_{35}$ intakt sind oder
(11) Kanten $K_{15}$ und $K_{25}$ und $K_{24}$ und $K_{34}$ intakt sind oder
(12) Kanten $K_{15}$ und $K_{45}$ und $K_{24}$ und $K_{23}$ intakt sind oder
(13) Kanten $K_{14}$ und $K_{45}$ und $K_{25}$ und $K_{23}$ intakt sind oder
(14) Kanten $K_{14}$ und $K_{24}$ und $K_{25}$ und $K_{35}$ intakt sind oder
(15) Kanten $K_{12}$ und $K_{24}$ und $K_{45}$ und $K_{35}$ intakt sind oder
(16) Kanten $K_{12}$ und $K_{25}$ und $K_{45}$ und $K_{34}$ intakt sind.
Diese Aufstellung ist identisch mit den 16 unterschiedlichen Pfaden der Längen 1 bis 4, die es in $K_5$ gibt. Die Anzahlen entsprechen obiger Tabelle.
Mit Hilfe von Maple habe ich für die vollständigen Graphen $K_3$ bis $K_5$ die Wahrscheinlichkeit berechnet, dass ein Signal von einem Knoten zu einem anderen Knoten durch das Netz (den Graphen) durchkommt. Dabei habe ich vorausgesetzt, dass die Wahrscheinlichkeit, dass eine Kante intakt ist, für alle Kanten gleich $p$ ist.
Das Maplesheet geht für jeden Graphen folgendermaßen vor:
a) $Xn$ Aufstellen eines logischen Ausdrucks, der die Intaktheit der möglichen Pfade in $K_n$ beschreibt. Dabei steht die logische Variable $Kij$ für die Aussage Kante $K_{ij}$ intakt.
b) $XnC$ Berechnung der kanonischen DNF zu $Xn$
c) $XnB$ Umsetzen der kanonischen DNF in einen Maple-internen logischen Ausdruck (um ihn als String behandeln zu können)
d) $XnS$ Umsetzen in einen String
e) $XnP$ Ersetzen der logischen Operatoren and -> *, or -> +; Ersetzen der logischen Variablen durch p; Ersetzen einer verneinten logischen Variablen durch (1-p) zu einem String in Form von einem algebraischen Ausdruck
f) $XnE$ Umformen des Strings in einen algebraischen Ausdruck
g) Vereinfachen des algebraischen Ausdrucks
Wir erhalten in jedem Falle ein Polynom in $p$. Die Tabelle zeigt die Ergebnispolynome, dahinter eine Abbildung mit den Polynomen.
$$
\begin{array}{c|c|c}
\text{n} & \text{Wahrscheinlichkeitspolynom} \\ \hline \hline
2 & p & schwarz\\ \hline
3 & -p^3 + p^2 + p & blau\\ \hline
4 & -2p^6 + 7p^5 - 7p^4 +2p^2 +p & grün\\ \hline
5 & 6p^{10} - 42p^9 +120p^8 -175p^7 +127 p^6-27p^5-15p^4+3p^3+3p^2+p &rot \\ \hline
\end{array}
$$
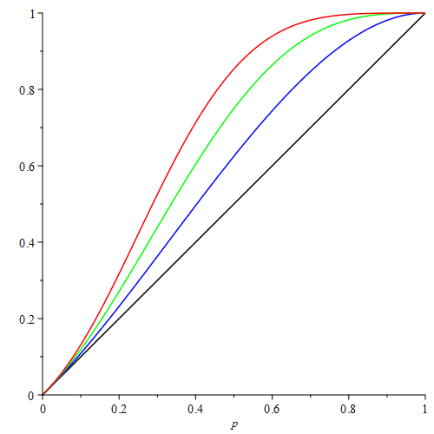
Wer möchte kann sich das Maple-Sheet ansehen, es wurde mit Maple 2022 erzeugt.
ZuGraph.pdf
Entscheidungsbäume zum Treffen strategischer Entscheidungen
Eine dritte Anwendung von Bäumen im Zusammenhang mit Wahrscheinlichkeiten sind Entscheidungsbäume, die einen Hinweis auf die beste Entscheidung liefern. Ein typisches und allgemein bekanntes Beispiel ist das Ziegenproblem, hier nochmal kurz dargestellt.
Hinter drei Türen stehen jeweils ein Auto und zwei Ziegen. Ein Kandidat kann das Auto gewinnen, wenn er die richtige Tür öffnet, nämlich die, hinter der das Auto steht. Der Moderator des Gewinnspiels baut aber eine zusätzliche "Schikane" ein. Nachdem sich der Kandidat für eine Tür entschieden (aber noch nicht geöffnet) hat, macht er zufällig eine Tür auf, hinter der eine Ziege steht - der Moderator kennt die Position von Auto und Ziegen - und fragt den Kandidaten, ob er seine Entscheidung noch revidieren und die andere, verbleibende Türe öffnen möchte. Was soll der Kandidat tun, bei der zuerst gewählten Tür bleiben oder wechseln?
Dies ist ein typisches Beispiel für das Treffen einer strategischen Entscheidung in Abhängigkeit von Wahrscheinlichkeitsannahmen.
Anders als bei den obigen Darstellungen ist der Ausgangspunkt, also die Wurzel des Baumes, die anstehende Entscheidung, hier Tür wechseln oder nicht.
In [32] habe ich eine sehr schöne Darstellung mit Erläuterung, wie der Entscheidungsbaum aufzubauen ist, gefunden, der ich das Endergebnis des Entscheidungsbaumes entnommen habe. Unter dem gleichen Logo "onlinedozent" findet sich auch ein Clip, der an einem Beispiel aus der Wirtschaft ausführlich die Methodik zum Aufbau eines Entscheidungsbaumes darstellt - sehr empfehlenswert.
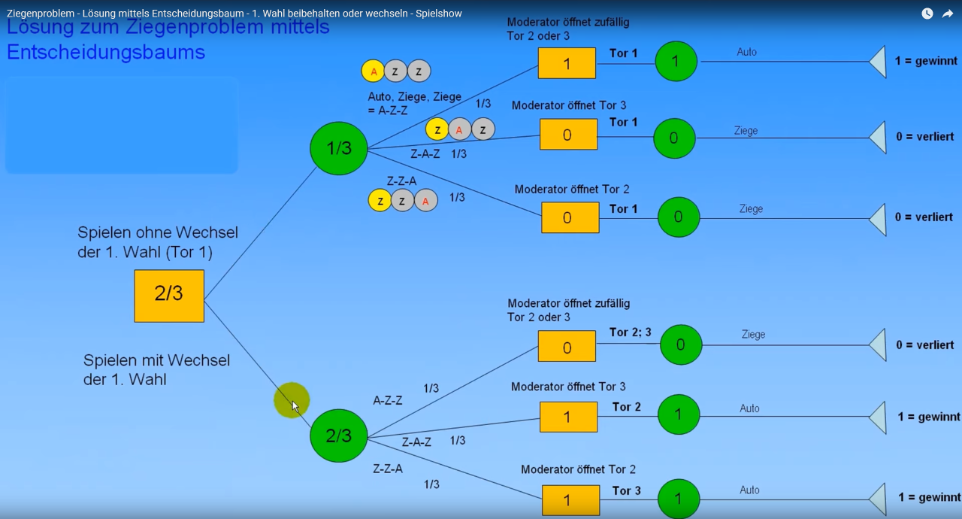
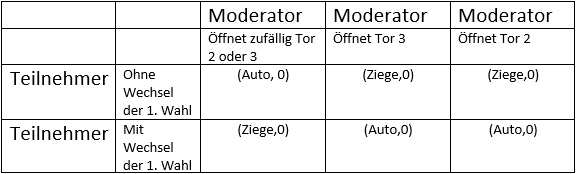
Ausgehend vom linken Rechteck, das die strategische Entscheidung darstellt, sind die möglichen Äste gezeichnet, die die Konsequenzen der Entscheidung darstellen und berechnen. Die grünen Kreise enthalten die Ergebnis-Wahrscheinlichkeiten der beiden Äste, dahinter sind die möglichen Fälle der Türöffnungen gezeichnet. Alternativ kann man auch eine sog. "Auszahlungsmatrix" aufstellen, wie sie aus der Spieltheorie bekannt ist.
Überhaupt ist die Spieltheorie oder auch Entscheidungstheorie eine Anwendung von Graphen; gegenüber der Darstellung als Auszahlungsmatrix kann der Baum auch eine zeitliche Abfolge der strategischen Entscheidungen darstellen. Aber dies ist eine andere Geschichte (oder besser ein anderer Aufsatz).
Man sieht, man weiss, der Wechsel zur anderen Tür ist die richtige Strategie.
5.2 Bäumchen wechsel Dich
$$
\pi: \mathbb{N}_n \rightarrow \mathbb{N}_n, \quad \pi((1,2,3,\cdots, n)) = (\pi(1), \pi(2), \pi(3), \cdots, \pi(n))
$$
auch geschrieben als:
$\left(
\begin {array}{ccccc}
1 & 2 & 3 & \cdots & n \\
\pi(1) & \pi(2) & \pi(3) & \cdots & \pi(n)
\end {array}
\right)$
Der Transfer in die Darstellung eines gerichteten Graphen erfolgt einfach durch Wahl der Knotenmenge $V=\mathbb{N}_n$ und Kantenmenge $E=\{(i,\pi(i))|i=1, \cdots, n\}$. In einem solchen Graphen hat jeder Knoten genau eine ausgehende und genau eine eingehende Kante, d.h. Ausgangsgrad und Eingangsgrad jedes Knoten sind 1.
Die speziellen Begriffe von Permutationen übertragen sich auf Graphen:
a) Ist $ \pi(i) = i$, also keine Fehlstellung bei i, dann hat der Graph beim Knoten i eine Schleife.
b) Eine Transposition $\tau(i) = j, \; \tau(j) = i$ ist eine ungerichtete Kante zwischen i und j.
c) Ein Zyklus einer Permutation entspricht einem Kreis im Graphen. (Bitte nicht Zyklus einer Permutation mit Zyklus in einem Graphen verwechseln!)
d) Betrachtet man die Zahlen, die durch die Permutation nicht verändert werden als spezielle Zyklen der Permutation, kann man sagen, dass eine Permutation genauso viele Zyklen hat, wie der zugehörige Graph Zusammenhangskomponenten.
e) Die identische Permutation entspricht dem Graphen der Ordnung n ohne Kanten.
Sei $\pi =
\left(
\begin{array}{ccccccc}
1 & 2 & 3 & 4 & 5 & 6 & 7 \\
2 & 4 & 1 & 3 & 5 & 7 & 6
\end{array}
\right)
$. Der zugehörige Graph sieht dann so aus:
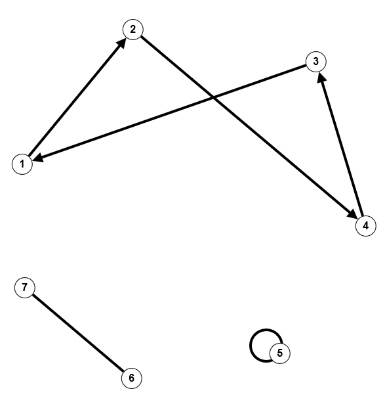

In der Darstellung als Graph erkennt man sehr schön die "Bahnen" der Permutation $1 \rightarrow 2 \rightarrow 4 \rightarrow 3 \rightarrow 1$ und $6 \rightarrow 7 \rightarrow 6$ und $ 5\rightarrow 5$.
Die Menge der Permutationen der ersten n nat. Zahlen bilden bezüglich der Hintereinanderausführung von Abbildungen eine Gruppe. Somit hat jede Permutation eine Inverse (rechter Graph). In obigem Beispiel erhält man den zu $\pi^{-1}$ gehörigen Graphen einfach durch Umkehren aller Richtungspfeile. Überhaupt kann man auf diese Weise auch in der Untermenge von Graphen der Ordnung n eine Gruppenstruktur definieren.
Eine weitere Eigenschaft lässt sich aus den Graphen erkennen. Bekanntlich ist die Hintereinanderausführung nicht kommutativ. Aber die beiden Ergebnisse $\pi \circ \rho$ und $\rho \circ \pi$ haben trotzdem eine Gemeinsamkeit, die sich aus der graphischen Darstellung als Baum ablesen lässt.
Wie man auch an obigem Beispiel sieht, bestehen die Graphen aus 3 Elementen
- isolierte Punkte (also identische Zuordungen in der Permutation)
- mit Hin- und Rückrichtung verbundene 2 Knoten (entspricht einer Transposition in der Permutation)
- Kreise (entspricht Zyklen in der Permutation).
Natürlich ist auch eine Transposition ein Zyklus (der Länge 2) und, wenn man will, ist auch eine identische Zuordnung ein Zyklus der Länge 1. Bekanntlich kann man jede Permutation in Zyklen zerlegen:
Satz 5.2 [34]
Jede Permutation der Länge n kann eindeutig (bis auf die Reihenfolge) als Hintereinanderausführung von paarweise disjunkten Zyklen geschrieben werden, in denen insgesamt alle Elemente von $\mathbb{N}_n$ vorkommen. Die Summe der Längen der beteiligten Zyklen ist gleich n.
Beispiel:
$$\pi =
\left(
\begin{array}{ccccccc}
1 & 2 & 3 & 4 & 5 & 6 & 7 \\
2 & 4 & 1 & 3 & 5 & 7 & 6
\end{array}
\right) = (1 2 4 3)(5)(67)$$
In diesem Zusammenhang definiert man nun den Zyklustyp einer Permutation wie folgt:
Definition 5.3 (Zyklustyp) [34]
Die Längen der Zyklen einer Permutation (gemäß Satz 4.16) definieren den Zyklustyp der Permutation. Man verwendet zur Darstellung einer Exponentenschreibweise (die nichts mit Potenzieren zu tun hat); die Basen sind die Zykluslängen, die Exponenten sind die Häufigkeit des Auftretens dieser Zykluslänge. Element mit Exponent 0 werden weggelassen.
Beispiel:
Der Zyklustyp von $\pi$ ist $1^12^14^1$. Die Inverse $\pi^{-1}$ hat den gleichen Zyklustyp. Die Identität hat den Zyklustyp $1^n$. Eine Permutation, die nur eine Transposition hat, hat den Zyklustyp $1^{n-2}2^1$.
Worauf will ich hinaus? Bei der Vertauschung zweier Permutationen ergeben sich in den Ergebnispermutationen die gleiche Anzahl von Zyklen gleicher Art (wenn auch an unterschiedlichen Stellen), mit anderen Worten $\pi \circ \rho$ und $\rho \circ \pi$ haben den gleichen Zyklustyp.
Dazu einige Beispiele.
$$\pi =
\left(
\begin{array}{cccccccccc}
1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\
7 & 2 & 3 & 4 & 5 & 6 & 1 & 8 & 9 & 10
\end{array}
\right)$$
$$\rho =
\left(
\begin{array}{cccccccccc}
1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\
6 & 1 & 4 & 5 & 3 & 10 & 7 & 8 & 9 & 2 \\
\end{array}
\right)$$
$$\pi \circ \rho =
\left(
\begin{array}{cccccccccc}
1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\
6 & 7 & 4 & 5 & 3 & 10 & 1 & 8 & 9 & 2 \\
\end{array}
\right)$$
$$\rho \circ \pi =
\left(
\begin{array}{cccccccccc}
1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\
7 & 1 & 4 & 5 & 3 & 10 & 6 & 8 & 9 & 2 \\
\end{array}
\right)$$
Die Graphen der Kompositionen sind:
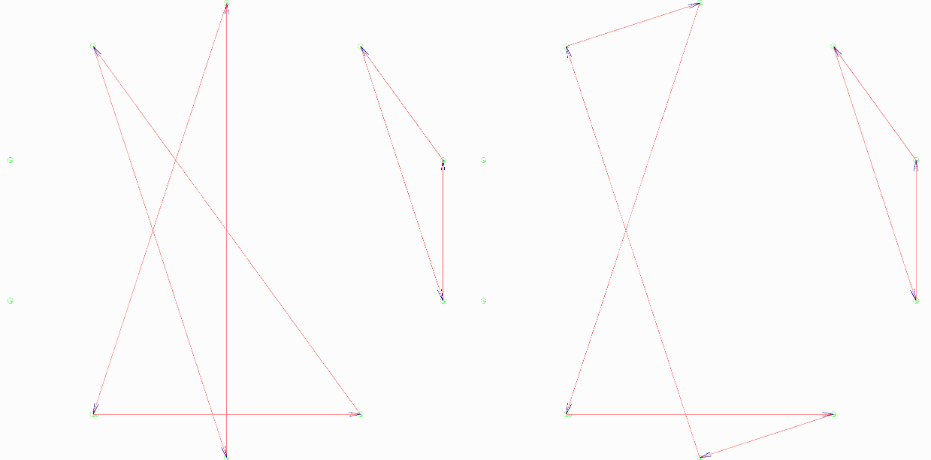
Sie bestehen beide aus einem 3er Kreis, einem 5er und 2 isolierten Punkten. Die Schleifen bei den isolierten Punkten habe ich nicht eingezeichnet, aber jeder isolierte Punkt hat eine. Gemeinsamer Zyklustyp: $1^23^15^1$.
Das nächste Beispiel hat 18 Knoten.
$$\pi=
\left(
\begin{array}{cccccccccccccccccc}
1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 & 17 & 18 \\
5 & 1 & 3 & 7 & 6 & 13 & 18 & 2 & 9 & 10 & 11 & 12 & 4 & 14 & 15 & 16 & 17 & 8 \\
\end{array}
\right)$$
$$\rho=
\left(
\begin{array}{cccccccccccccccccc}
1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 & 17 & 18 \\
9 & 18 & 3 & 4 & 5 & 6 & 7 & 8 & 1 & 10 & 17 & 12 & 13 & 14 & 15 & 16 & 11 & 2 \\
\end{array}
\right)$$
$$\pi \circ \rho=
\left(
\begin{array}{cccccccccccccccccc}
1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 & 17 & 18 \\
9 & 8 & 3 & 7 & 6 & 13 & 18 & 2 & 5 & 10 & 17 & 12 & 4 & 14 & 15 & 16 & 11 & 1 \\
\end{array}
\right)$$
$$\rho \circ \pi=
\left(
\begin{array}{cccccccccccccccccc}
1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 & 17 & 18 \\
5 & 9 & 3 & 7 & 6 & 13 & 2 & 18 & 1 & 10 & 17 & 12 & 4 & 14 & 15 & 16 & 11 & 8 \\
\end{array}
\right)$$
Die Graphen der Komposition sind:
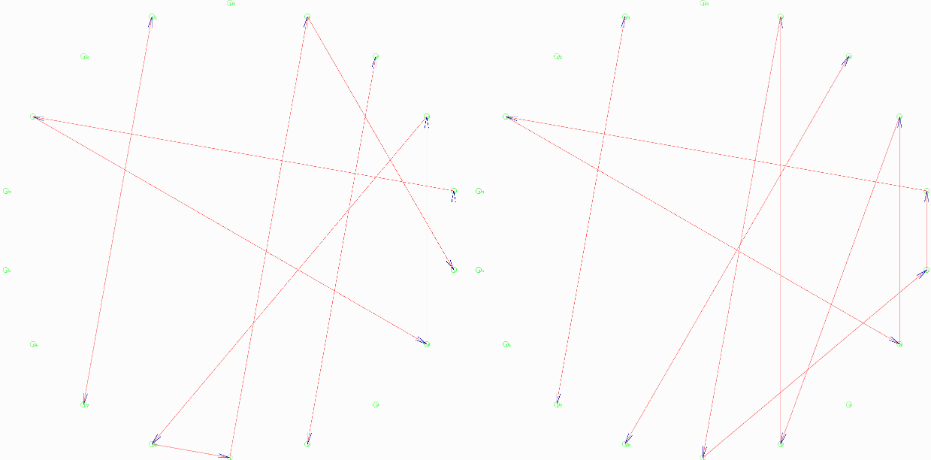
Sie bestehen beide aus einem 8er Kreis, zwei 2er Kreisen und 6 isolierten Punkten. Der gemeinsame Zyklustyp ist $1^62^28^1$.
Diese Eigenschaft ist kein Zufall, denn es gilt der folgende Satz:
Definition 5.4 (konjugiert)
Zwei Permutationen $\pi$ und $\rho$ sind konjugiert, wenn es eine Permutation $\sigma$ gibt, s.d. gilt $\pi \circ \sigma = \sigma \circ \rho$ oder auch $\pi = \sigma \circ \rho \circ \sigma^{-1}$.
Satz 5.5 [34]
Zwei Permutationen sind genau dann konjugiert, wenn sie den gleichen Zyklustyp haben.
Nun sind aber $\pi \circ \rho$ und $\rho \circ \pi$ immer konjugiert, denn es gilt: $\pi \circ \rho = \pi \circ (\rho \circ \pi) \circ \pi^{-1}$.
Somit folgt, dass $\pi \circ \rho$ und $\rho \circ \pi$ immer den gleichen Zyklustyp haben.
5.3 Nach Adam Riese
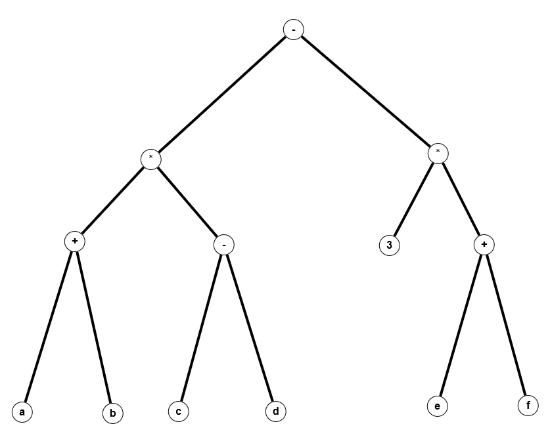 $(a+b)*(c-d)-3*(e+f)$
$(a+b)*(c-d)-3*(e+f)$Das Setzen der Klammern kann mit einfachen Regeln unterstützt werden. Ein Maximalprogramm wird einfach durch die Regel
- Klammern werden immer an einer Verzweigung in die nächste Ebene gesetzt.
Mit
- Ein äußerstes Klammerpaar kann weggelassen werden.
- Bei der Verbindung zweier Ausdrücke mit * oder / brauchen keine Klammern gesetzt werden.
Damit kommt man schon zu $(a+b) * (c-d) -3*(e+f)$. Unäre Operatoren oder Funktionen können ebenfalls eingezeichnet werden, dann hat ein Knoten nur einen Kindknoten. Statt dessen kann man die Funktion auch an die Kante schreiben, was aber eher ungebräuchlich ist; warum sehen wir gleich.
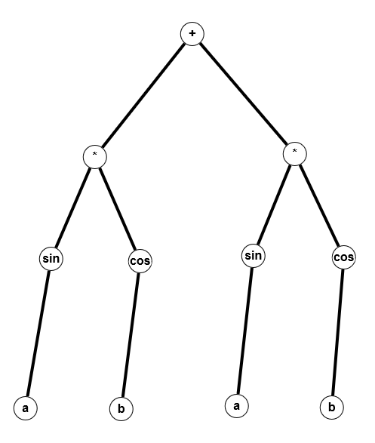
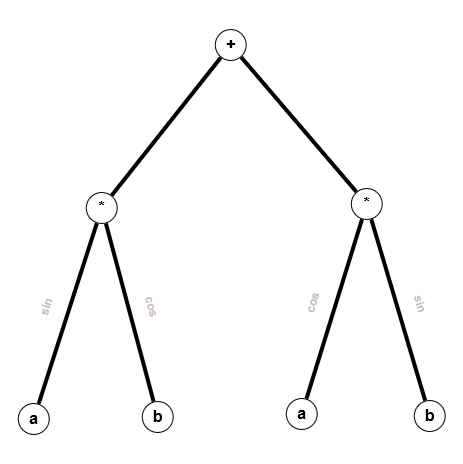 $sin(a) * cos(b)+cos(a)*sin(b)$
$sin(a) * cos(b)+cos(a)*sin(b)$Bei (binären) Bäumen gibt es generell 3 verschiedene Möglichkeiten den Baum zu durchlaufen (traversieren), sie heißen Preorder, Inorder und Postorder. Transferiert auf unsere "Formelbäume" entspricht dies der Frage wo die Operatoren in dem entstehenden Ausdruck stehen, wenn man sie beim Durchlaufen hinschreibt. Das Durchlaufen beginnt man bei der Wurzel und fährt wie mit einem Auto in Fahrtrichtung rechts von den Kanten und Knoten am Baum entlang, bis man zum dritten Mal wieder bei der Wurzel ankommt (den Start mitgezählt). Jeder Knoten bekommt 3 Nummern 1, 2, und 3, die 1 links vom Knoten, die 2 unter dem Knoten, die 3 rechts neben dem Knoten. Ein Bild sagt mehr als 1000 Worte [33]:
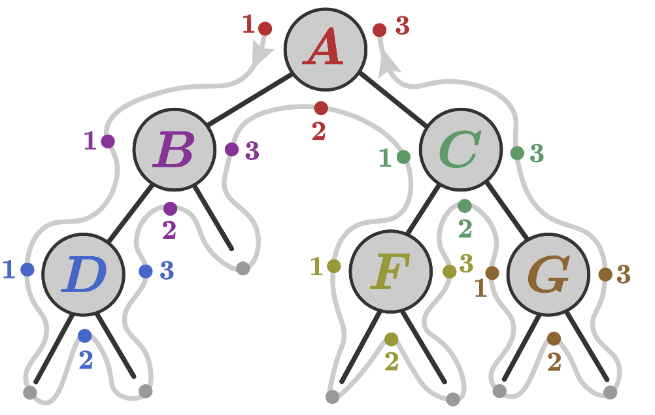
Fangen wir mit der Preorder an: (Faustregel: Vaterknoten, linker Kindknoten, rechter Kindknoten). Beim Preorder-Durchlauf nimmt man die Knoten in die Reihenfolge auf, wenn man zum ersten mal bei ihnen vorbeikommt (linke Nummer 1), also A, B, D, C, F, G. Natürlich wird kein Knoten doppelt aufgeführt.
Bei der Inorder (linker Kindknoten, Vaterknoten, rechter Kindknoten) nimmt man den Knoten auf, wenn man zum zweiten Mal an ihm vorbeikommt (untere Nummer 2), also D, B, A, F, C, G.
Und bei der Postorder (linker Kindknoten, rechter Kindknoten, Vaterknoten), nimmt man den Knoten auf, wenn man zum dritten Mal an ihm vorbeikommt (rechte Nummer 3), also D, B, F, G, C, A.
Super Darstellung vom Universaldenker!
Das wenden wir jetzt gleich mal auf den obigen arithmetischen Baum an:
Zunächst die Inorder: a + b * c - d - 3 * e + f. Das ist, bis auf die Klammern, genau die gewohnte Schreibweise des Ausdruckes; die Operatoren stehen zwischen den Operanden an den richtigen Stellen.
Bei der Preorder stehen die Operanden am Anfang: - * + a b - c d * 3 + e f.
Aber nun zur wichtigen Postorder: a b + c d - * 3 e f + * -. Hier stehen die Operatoren hinten. Diese Darstellung ist im Gegensatz zur Inorder klammerfrei möglich, d.h. in dieser Darstellung führt sie zum korrekten Ergebnis. Die Klammerfreiheit gilt übrigens auch für die Preorder Darstellung. Der polnische Mathematiker Jan Lukasiewicz hat die Preorder-Darstellungen in den 20er Jahren des letzten Jahrhunderts entwickelt, eben gerade mit dem Ziel, klammerfreie Darstellungen von Ausdrücken zu erhalten. Man nennt die Preoder-Form auch "Polnische Notation", die Postorder "Umgekehrt polnische Notation" (UPN). Die Firma Hewlett Packard hat die UPN zur Grundlage für die Eingabe in ihre Taschenrechner gemacht. Ich selber habe in den 70er Jahren ein solches Gerät besessen (HP 41) und während des Studiums heftig verwendet. Ich trauere dem Gerät heute noch nach, warum? Wegen der Eingabemöglichkeit in UPN - klammerfrei. Das Gerät hatte einen Stack (Kellerspeicher) aus 4 Speichern (x,y,z und t). Die Bedienung erfolgt mit Hilfe einer ENTER-Taste, die eine im Display eingegebene Zahl (das Display entsprach dem x-Speicher) in den Stack drückte (und alle tieferen eine Stufe nach unten) und damit das Display für die nächste Zahleneingabe freimachte. Eine binäre Operation bezog sich dann immer auf die obersten beiden Stacks, also y und x und lieferte das Ergebnis in x, also im Display ab; die darunter liegenden Werte wurden dann im Stack wieder eine Stufe nach oben gezogen.
Im Beispiel: Die Eingabe 3 ENTER 4 + addiert also die Zahlen 3 und 4 und liefert das Ergebnis 7. Eine Gleichheitstaste gibt es ebenfalls nicht, da jede Operation das Ergebnis sofort nach sich zieht. Unser obiger Rechenbaum wird also in folgender Weise eingegeben: a ENTER b + ENTER c ENTER d - * ENTER 3 ENTER e ENTER f + * -. Dass der Stack nicht überläuft liegt daran, dass jede Operation den Stack ja wieder nach "oben" rutschen lässt. HP hat noch eine weitere Vereinfachung eingebaut. wenn man ein Ergebnis durch Betätigen einer Operatortaste erhalten hat, kann man die nächste Zahl ohne erneutes ENTER eingeben. Wenn man (3+4)*5 rechnen will, muss man also nicht "3 ENTER 4 + ENTER 5 *" eingeben, sondern kann sich das zweite ENTER sparen: "3 ENTER 4 + 5 *". So spart man in obigem Ausdruck die beiden ENTER hinter den Rechenzeichen + und *.
Weil es so schön ist, habe ich einen kleinen Rechner, der UPN nutzt, programmiert und dazu auch eine Umsetzung eines Rechenbaumes in UPN. Als Werkzeug habe ich hier Excel mit VBA verwendet, denn Excel liefert die Darstellung der Oberfläche und den notwendigen Speicher gleich mit und hat eine einfache Verarbeitung von aktiven Elementen (Buttons, etc.).

Auf der linken Seite eine Eingabetastatur mit Ziffern binären Operatoren und der Enter-Taste, rechts die unären Operatoren mit den üblichen Funktionen. Die Taste "inv" liefert (außer bei 1/x) die Umkehrfunktionen. "hyp" schaltet bei "sin", "cos", "tan" und "cot" auf die hyperbolischen Funktionen um; "inv" und "hyp" schaltet auf die Umkehrfunktionen der hyperbolischen Funktionen (area) um. "Rad/°" ändert die Interpretation einer Eingabe von Bogenmaß auf Grad (Toggle). "Rad<->°" rechnet die Eingabe auf Grad , "inv Rad<->°" auf Bogenmaß um.
Der Stack umfasst 10 Speicher, die ersten 4 - es werden in der Praxis selten mehr benötigt - habe ich nostalgisch mit x, y, z und t bezeichnet.
Auf der rechten Seite ist ein kleiner Baum mit einem Beispiel gefüllt. Man kann die Einträge löschen und durch eigene ersetzen. "Start" und "Weiter" bauen schrittweise die zugehörige UPN auf; mit "Baum berechnen" wird dann das Ergebnis im Anzeigefeld oben links eingeblendet.

Will man die reine Postorder sehen, muss man sich die "Enter" - Einträge einfach wegdenken.
Der Aufwand zur Entwicklung des UPN-Rechners (ModulUPN) ist vergleichsweise gering; die Notwendigkeit einen klammerbehafteten arithmetischen Ausdruck syntaktisch zu zerlegen entfällt durch die UPN-Eingabe. Eine direkte Eingabe in das Anzeigefenster ist nicht sinnvoll, da bei der Eingabe programmintern bestimmte Prüfungen und Festsetzungen gemacht werden. Bei einer fehlerhaften Eingabe wird eine Meldung im Anzeigefenster ausgegeben und die Berechnung abgebrochen.
Um das Excel-Sheet benutzen zu können muss man Excel mitteilen, dass man mit der Ausführung von Makros einverstanden ist.
Dazu: Datei -> Optionen -> Trust Center -> Einstellungen für das Trust Center -> Makroeinstellungen -> Alle Makros aktivieren.
Anbei das Excel-Sheet für eigene Versuche, wie immer ohne Gewähr.
UPN.xlsm
6 Das Beste kommt zum Schluss
Sei $n \in \mathbb{N}, \; n > 1$ die Breite eines Elementarquadrates, so will ich es mal nennen, das die Zahlen von $1 \text{ bis } n^2$ enthalten soll, hier für $n=3$, der häufigsten Ausprägung des Spiels:
| 3 |
4 |
9 |
| 2 |
1 |
6 |
| 5 |
7 |
8 |
Ein vollständiges Sudoku besteht nun aus $n^2$ solcher Elementarquadrate, die wieder zu einem Quadrat zusammengesetzt werden:

Obiges Bild zeigt den Anfangszustand eines Spiels, bei dem gewisse Anfangszahlen vorgegeben sind. Ziel des Spieles ist es jetzt, die offenen Felder so auszufüllen, dass
(i) in jedem Elementarquadrat alle $n^2$ Zahlen (hier 9) genau einmal vorkommen,
(ii) in jeder Zeile alle $n^2$ Zahlen (hier 9) genau einmal vorkommen,
(iii) in jeder Spalte alle $n^2$ Zahlen (hier 9) genau einmal vorkommen.
Das setzt natürlich voraus, dass die vorgegebenen Zahlen diese Regeln bereits erfüllen. Je weniger Zahlen vorgegeben sind, desdo schwieriger ist die Aufgabe, wobei es da natürlich eine untere Grenze gibt, denn wenn man ein leeres Quadrat vorgibt, braucht man ja nur eine vorhandene Lösung eintragen. Folgende Fragen stellen sich wie bei jeder mathematischen Aufgabe:
A) Wieviel verschiedene fertig gefüllte Sudokus gibt es?
C) Gibt es zu einem vorgegebenen Anfangszustand immer eine Lösung?
C) Ist eine gefundene Lösung eindeutig?
D) Gibt es eine Strategie (Algorithmus) zum Lösen einer solchen Aufgabe?
Die Antworten auf diese Fragen hängen natürlich von n ab und von der Anzahl der vorgegebenen Anfangszahlen. Betrachten war aber zunächst die Frage, was überhaupt "verschiedene Sudokus" bedeutet, denn viele Sudokus sind zwar voneinander verschieden, gehen aber durch unterschiedliche Manipulationen auseinander hervor, d.h. sie unterscheiden sich nicht strukturell voneinander. Vertauscht man z.B. in einem fertigen Sudoku zwei Zahlen, dann entsteht zwar eine neue Lösung, aber sie sind strukturell nicht unterschiedlich. Entsprechend kann man durch Vertauschen von Zeilen, Spalten oder Elementarquadraten unterschiedliche, aber nicht strukturell unterschiedliche Lösungen erreichen. Auch Spiegelungen oder Drehungen führen zu nichts Neuem mehr. All dieses ausgeschlossen, gibt es für $n=3$ (nach Russel und Jarvis 2006) rund 5,5 Milliarden verschiedene Sudokus [36]. Bei $n=2$ sind es (nach Herzberg und Murty) nur 2 (!) strukturell verschiedene Rätsel [37].
Zur Frage B) der Existenz einer Lösung habe ich bisher keine Aussage finden können. Klar ist aber, dass nicht jede korrekte Vorgabe eine Lösung hat. Betrachtet man z.B. das 2er - Sudoku
| 1 |
4 | ||
| 2 |
|||
| 4 | 1 | 2 | |
| 3 |
dann ist die Vorgabe als solche nicht fehlerhaft, aber man sieht sehr schnell, dass es keine Lösung geben kann, denn bei der zwingenden Eintragung einer 4 in das Feld (4, 3) widerspricht dies der 4 in (1, 3).
zu C): Für die Eindeutigkeit allerdings gibt es eine Aussage [36] [37]. Bei n=3 gibt es bei 16 vorgegebenen Startzahlen keine eindeutige Lösung. Dies wurde mit Hilfe eines Computerbeweises nachgewiesen, der allerdings noch nicht durch andere verifiziert ist. Bei 17 Vorgabezahlen gibt es Sudokus, die nur eine eindeutige Lösung zulassen. Klar ist aber auch, dass für eine eindeutige Lösung mindestens 8 der 9 Ziffern zu den Vorgabezahlen gehören müssen, da sonst durch Vertauschung (s.o.) die Eindeutigkeit falsifiziert wird.
Wo bleibt die Graphentheorie?
Wir sind schon mitten drin, aber ich habe bisher noch nichts dazu gesagt. Aber jetzt!
Ein Sudoku lässt sich nämlich durch einen chromatischen Graphen beschreiben. Hierbei ordnet man jedem der $n^4$ Felder eines n - Sudoku einen Knoten eines Farbgraphen zu, also einem 2er - Sudoku 16 Knoten; am einfachsten nummeriert man die Felder von 1 bis $n^4$ durch und erhält die entsprechenden Knotennummern. Das folgende Bild aus [38] zeigt dies für n=2:
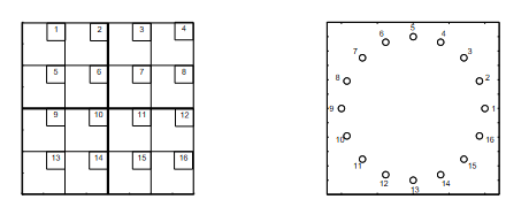
Nun verbindet man im Farbgraphen die Knoten miteinander, in denen die zugehörigen Felder des Sudokus nicht die gleichen Zahlen auftreten dürfen, also z.B. die 1 mit 2, 3, 4 (1. Zeile) und 5, 9, 13 (1. Spalte) und 2, 5, 6 (1. Elementarquadrat). Schon verbundene Knoten werden nicht nochmal verbunden (kein Mehrfachgraph, siehe auch Satz 4.20). Nun identifiziert man die $n^2$ - vielen Ziffern, die man in das Sudoku eintragen kann mit entsprechend vielen Farben. Das Ausfüllen der Zellen eines Sudoku entspricht also der Färbung der Knoten des Farbgraphen.
Die aus dem Kapitel über das chromatische Polynom bekannte Fragestellung lautet nun: Mit wieviel unterschiedlichen Farben kann ich den Farbgraphen einfärben, sodass zwei verbundene Kanten nicht die gleich Farbe haben? Dies entspricht auf der Seite des Sudokus der Frage: Wieviel Ziffern brauche ich um das Sudoku gemäß obigen Regeln zu füllen? Dies sollten natürlich $n^2$ - viele sein, aber man kann natürlich das Problem des Farbgraphen erst einmal losgelöst betrachten und das will ich hier tun - schließlich habe ich ja ein Programm, das ein chromatisches Polynom berechnet und daraus ergibt sich ja die chromatische Zahl, eben diese Mindestzahl der notwendigen Farben.
Aber vorher notieren wir noch folgenden Satz:
Satz 6.1
Ein aus einem n - Sudoku abgeleiteter Farbgraph ist $3n^2 - 2n - 1$ - regulär.
Um das Programm anzuwenden braucht man erstmal eine Adjazenzmatrix des Farbgraphen. Das allein ist für n = 2 von Hand schon ziemlich aufwändig, für größere n nicht mehr sinnvoll machbar. Also brauche ich auch hier ein Programm, das zunächst die Adjazenzmatix liefert. Das habe ich geschrieben und für n = 2 erhalte ich:
0,1,1,1,1,1,0,0,1,0,0,0,1,0,0,0
1,0,1,1,1,1,0,0,0,1,0,0,0,1,0,0
1,1,0,1,0,0,1,1,0,0,1,0,0,0,1,0
1,1,1,0,0,0,1,1,0,0,0,1,0,0,0,1
1,1,0,0,0,1,1,1,1,0,0,0,1,0,0,0
1,1,0,0,1,0,1,1,0,1,0,0,0,1,0,0
0,0,1,1,1,1,0,1,0,0,1,0,0,0,1,0
0,0,1,1,1,1,1,0,0,0,0,1,0,0,0,1
1,0,0,0,1,0,0,0,0,1,1,1,1,1,0,0
0,1,0,0,0,1,0,0,1,0,1,1,1,1,0,0
0,0,1,0,0,0,1,0,1,1,0,1,0,0,1,1
0,0,0,1,0,0,0,1,1,1,1,0,0,0,1,1
1,0,0,0,1,0,0,0,1,1,0,0,0,1,1,1
0,1,0,0,0,1,0,0,1,1,0,0,1,0,1,1
0,0,1,0,0,0,1,0,0,0,1,1,1,1,0,1
0,0,0,1,0,0,0,1,0,0,1,1,1,1,1,0
Das ist ziemlich unübersichlich und deshalb stelle ich lieber mal den zugehörigen vollständigen Farbgraphen dar, er hat 16 Knoten (natürlich) und 56 Kanten.
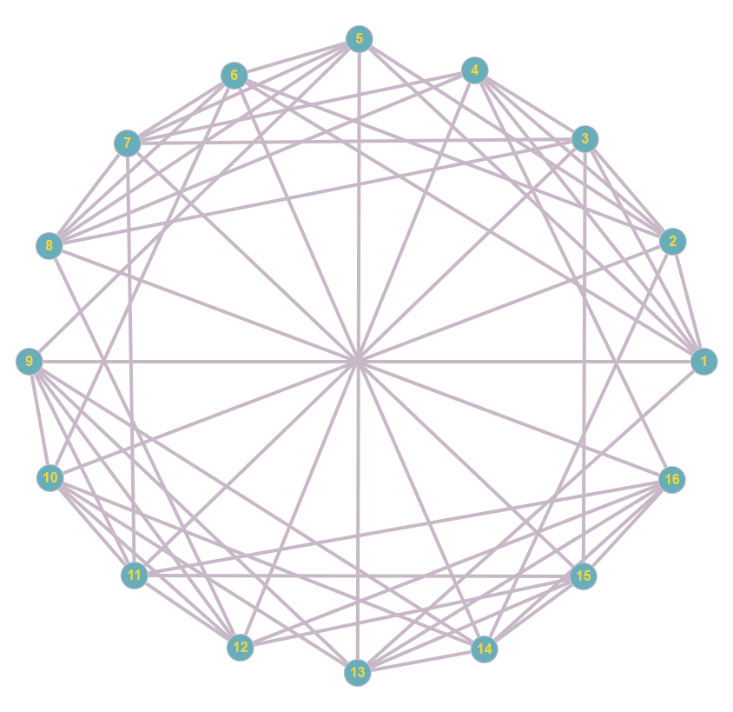
Ob es sinnvoll ist, auch für ein 3er - Sudoku (und höhere), die Adjazenzmatrix und den Farbgraphen anzugeben, mag jeder selber entscheiden; in [39] findet man eine solche Darstellung des Farbgraphen für n = 3. Die Anzahl der Kanten beträgt 810.
So jetzt kann ich die Adjazenzmatrix benutzen, um das chromatische Polynom zu berechnen. Aber langsam, die Matrix ist bereits so groß, dass die Berechnung, die ja rekursiv erfolgt und damit den sog. Heap des Pasacalprogrammes stark füllt, ohne weitere Tuningmaßnahmen locker sprengt. Der Heap auf meinem Rechner hat die maximale Größe eines durch 4 Byte adressierbaren Adressraumes, also Hexadezimal $FF FF FF FF_{16}$, was 4 GigaByte entspricht. Erst nach einer Fülle speicherplatzsparender Eingriffe in den Code, konnte ich das chromatische Polynom auf der Basis der vollständigen Graphen berechnen - der Weg über die Bäume wurde weiterhin durch einen Heap-Overflow blockiert. Aber so reicht es ja und ich erhielt:
a)
$$
\chi(P,k) = 1 \cdot \chi(K_{16},k) + 64 \cdot \chi(K_{15},k) + 1632 \cdot \chi(K_{14},k) + 21520 \cdot \chi(K_{13},k) + 159664 \cdot \chi(K_{12},k) +
681616 \cdot \chi(K_{11},k) + 1651576 \cdot \chi(K_{10},k) +
$$
$$
2173088 \cdot \chi(K_{9},k) + 1435536 \cdot \chi(K_{8},k) + 420528 \cdot \chi(K_{7},k) +
45200 \cdot \chi(K_{6},k) + 1376 \cdot \chi(K_{5},k) + 12 \cdot \chi(K_{16},k)
$$
b) -
c)
$$
\chi(P,k) = k^{16} - 56 k^{15} + 1492 k^{14} - 25072 k^{13} + 296918 k^{12} -2621552 k^{11} + 177995572 k^{10} -94352168 k^{9} +
$$
$$
392779169 k^{8} - 1279118840 k^{7} + 3217758336 k^6 - 6107865464 k^5 +8413745644 k^4 - 7877463064 k^3 + 4436831332 k^2 -1117762248 k
$$
d)
$$
\chi(P,k) = k(k - 1) (k - 2) (k-3)(k^{12} - 50 k^{11} + 1181 k^{10} -17430 k^9 + 179047 k^8 - 1348454 k^7 +
$$
$$
7630751 k^6 - 32660386 k^5 + 104787868 k^4 - 245342880 k^3 + 397072192 k^2 - 397933424 k + 186293708
$$
Wie man an d) sieht, ist die chromatische Zahl für das 2er - Sudoku tatsächlich k = 4.
Natürlich ist an eine Berechnung für das 3er - Sudoku oder größere mit meinem Programm nicht zu denken. Aber es lässt sich auch direkt beweisen, dass man für einen Farbgraph aus einem n - Sudoku $n^2$ vielen Farben zum Einfärben braucht (siehe z.B. [40]).
Bevor ich mich der obigen Frage D) zuwende, möchte ich noch ein weiteres Ergebnis zu Farbgraphen (Adjazenzmatrizen) aus n - Sudokus referieren. Ich fand einen Aufsatz, der eine Aussage über die Eigenwerte von solchen Graphen macht. [41] Abgesehen von der Aussage über die Eigenwerte, die ich gleich referieren werde, ist der Aufsatz auch interessant, weil er verschiedene mathematische Teilgebiete mit der Graphentheorie verbindet. Die Autoren nennen die Kombinatorik, die Algebra, genauer die Gruppentheorie und die lineare Algebra. Dabei werden spezielle endliche Gruppen betrachtet, aus denen Graphen abgeleitete werden, sog. Cayley-Graphen. Farbgraphen aus Sudoku sind solche Cayley-Graphen und über sie wird bewiesen:
Satz 6.2
Der Farbgraph eines n - Sudokugraphen hat folgende Eigenwerte (absteigend sortiert, algebraische Vielfachheiten darunter):
$$
\begin{array} {cccccc}
3n^2-2n-1 & 2n^2 -2n -1 & n^2 -n -1 & n^2 - 2n - 1 & -1 & -n-1 \\ \hline
1 & 2(n-1) & 2(n-1)n & (n-1)^2 & (n-1)^2n^2 & 2(n-1)^2n
\end{array}
$$
Für die Farbgraphen der 2er und 3er Sudokus ergibt sich:
$$
\begin{array} {c | c | c | c | c | c | c}
n= 2 & 7 & 3 & 1 & -1 & -1 & -3 \\ \hline
& 1 & 2 & 4 & 1 & 4 & 4 \\ \hline
n=3 & 20 & 11 & 5 & 2 & -1 & -4 \\ \hline
& 1 & 6 & 12 & 4 & 36 & 24 \\
\end{array}
$$
Interessanterweise ist der größter Eigenwert auch gleichzeitig der gemeinsame Knotengrad des Graphen (Satz 4.20).
Doch nun zur Berechnung der Lösungen eines Sudoku. Es gibt verschiedene Wege dies zu tun, ich habe einen Backtracking-Algorithmus programmiert, also eine "Try and Error" - Variante. Backtracking ist eine bekannte Methode zur Lösung von Rätselaufgaben, wie z.B. das 8-Damen Problem oder den Weg eines Springers auf einem Schachbrett [42]. In unserer Aufgabenstellung wird ein noch leeres Feld des Sudokuquadrates mit dem nächsten noch nicht ausprobierten Zahlenwert gefüllt und geprüft, ob dieser Wert den Sudokuregeln gehorcht. (Eine solche Versuchsserie pro Feld wird in der Prozedur tryNext gemacht.) Wenn ja, geht's zum nächsten Feld, wenn nein, löscht man den eingetragenen Wert und probiert den nächsten. Wenn keiner der $n^2$ Zahlen passt, dann muss der vorherige Wert gelöscht werden und durch den nächsten Kandidaten ersetzt werden usw. Und so kommt es zu einem ständigen Hin- und Her, das auch dazu führen kann, dass der überhaupt erste eingetragene Wert ausgetauscht wird und im schlimmsten Fall so oft, dass da kein korrekter Eintrag möglich ist. Dann ist das Sudoku unlösbar. Kommt das Programm andererseits am letzten leeren Feld an und findet einen korrekten Eintrag, dann haben wir eine Lösung.
Das Programm verlangt zunächst die Eingabe der Vorgabezahlen und zeigt dann das zu lösende Sudoku an. Als Ausgabe wird entweder das fertig ausgefüllte Sudoku angezeigt oder die Meldung zur Unlösbarkeit. In beiden Fällen wird die Anzahl der Versuche (Aufrufe tryNext) das nächste Feld zu füllen angezeigt; natürlich kommt es oft vor, dass dasselbe Feld in dem Hin und Her mehrfach geprüft wird. Jedenfalls ist diese Anzahl ein Indikator für die Kompliziertheit der Aufgabenstellung. Darüber hinaus wird der Füllungsgrad des Heap ausgegeben. Hier zunächst ein paar Beispiele.
Beispiel 1: 2er Sudoku Beispiel 2: 2er Sudoku (unlösbar)
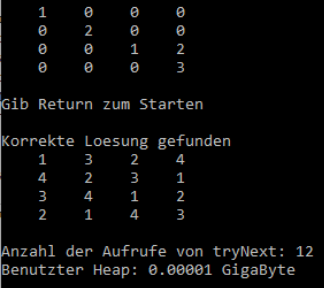
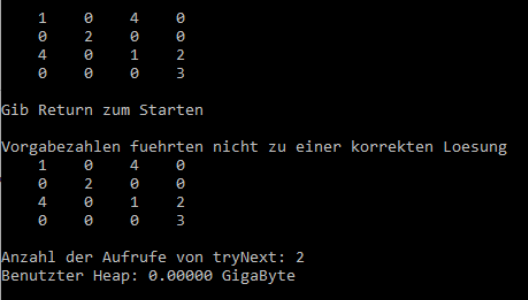
Beispiel 3: 3er Sudoku (leicht)
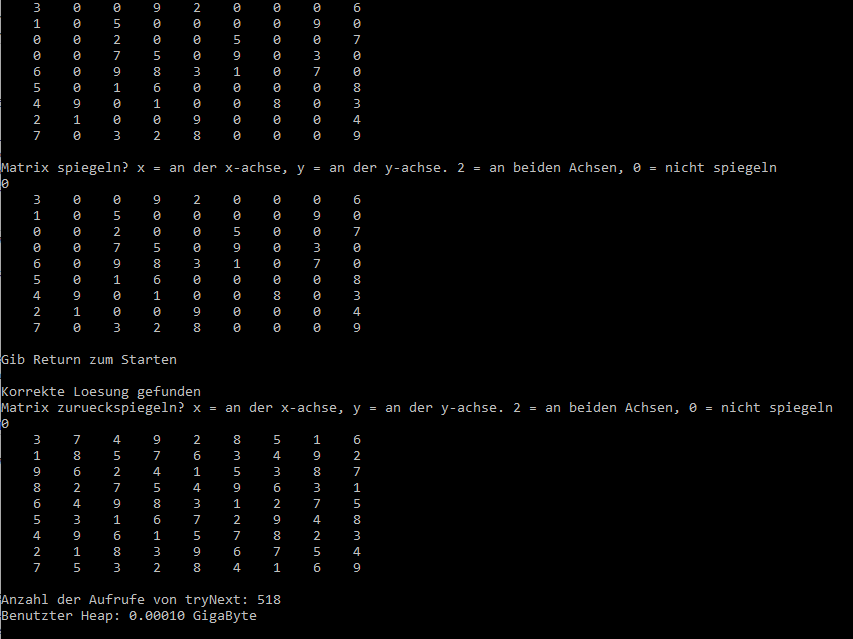
Bei einem 3er Sudoku ermöglicht das Programm eine Spiegelung des Vorgabesudokus; darauf komme ich gleich noch zurück.
Beispiel 4: 3er Sudoku (schwer)
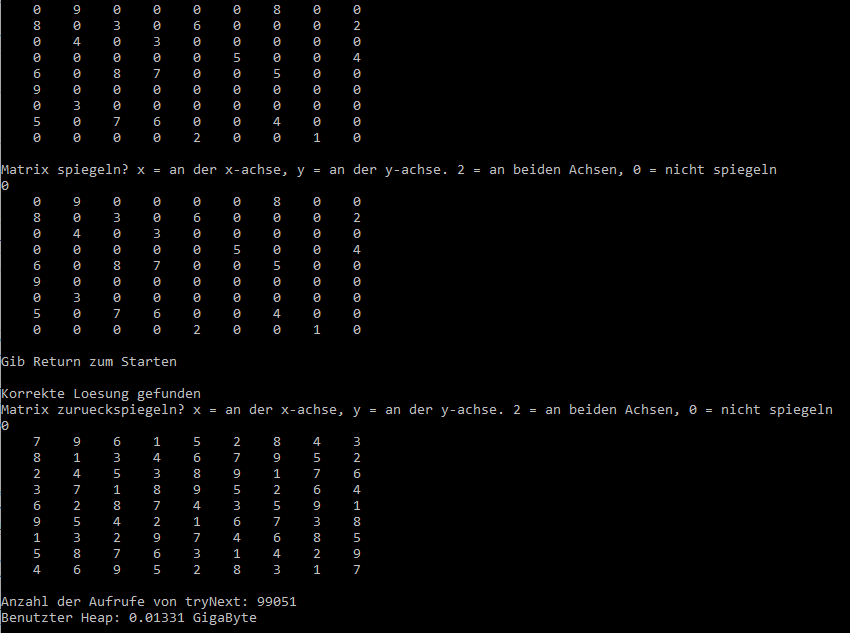
Im Vergleich zu Beispiel 3 werden hier viel mehr Aufruf von tryNext gemacht mit entsprechend höherem Speicherplatzbedarf im Heap.
Das nächste Beispiel geht nun an die Grenzen des Programmes. Es ist ein Beispiel, das ich in [43] gefunden habe; es zeigt den Fall von 17 Vorgabezahlen bei eindeutiger Lösung. So wie das Beispiel bei Wikipedia abgedruckt ist, meint mein Programm, dass die maximale Größe des Heap überschritten wird:

Dies liegt wohl daran, dass die ersten 3 Zeilen jeweils nur eine Vorgabezahl enthalten und mein Programm mit den Füllungsversuchen oben links beginnt und dann zeilenweise weitermacht. Deshalb kam ich auf die Idee, die Vorgabematrix zu spiegeln und siehe da, es funktioniert, denn die nach dem Spiegeln an der 5. Zeile oben stehenden Zeilen enthalten mehr Vorgabezahlen.
Beispiel 5: (17 Vorgabezahlen, gespiegelt an der Waagrechten durch die Zeile 5)
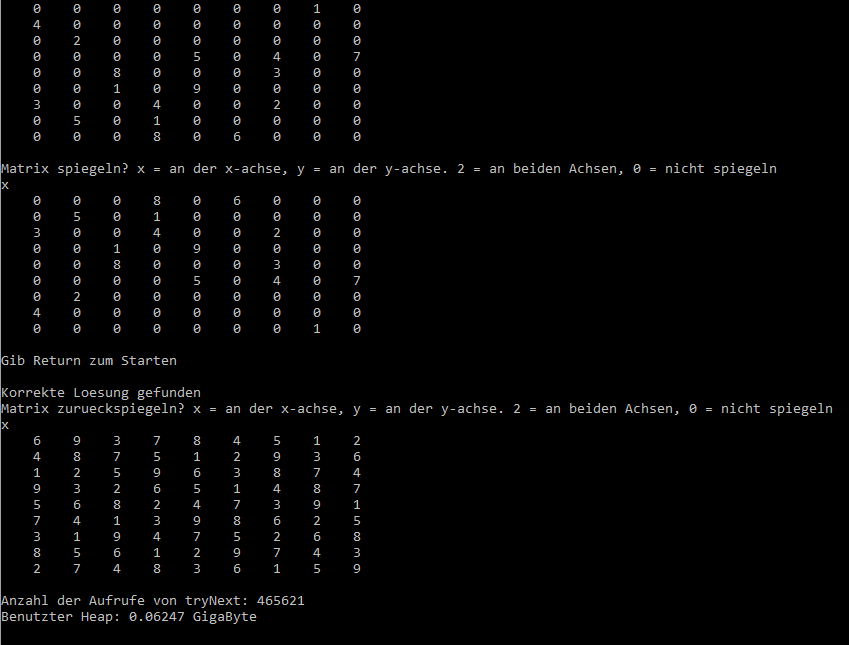
Die Anzahl der tryNext - Aufrufe ist stark nach oben gegangen (im gleichen Verhältnis die Heap-Auslastung). Noch etwas geringer ist die Anzahl der Trys, wenn man an einmal waagrecht und dann senkrecht spiegelt:
Beispiel 6: (17 Vorgabezahlen, gespiegelt an der Waagrechten durch die Zeile 5 und an der Senkrechten durch Spalte 5)
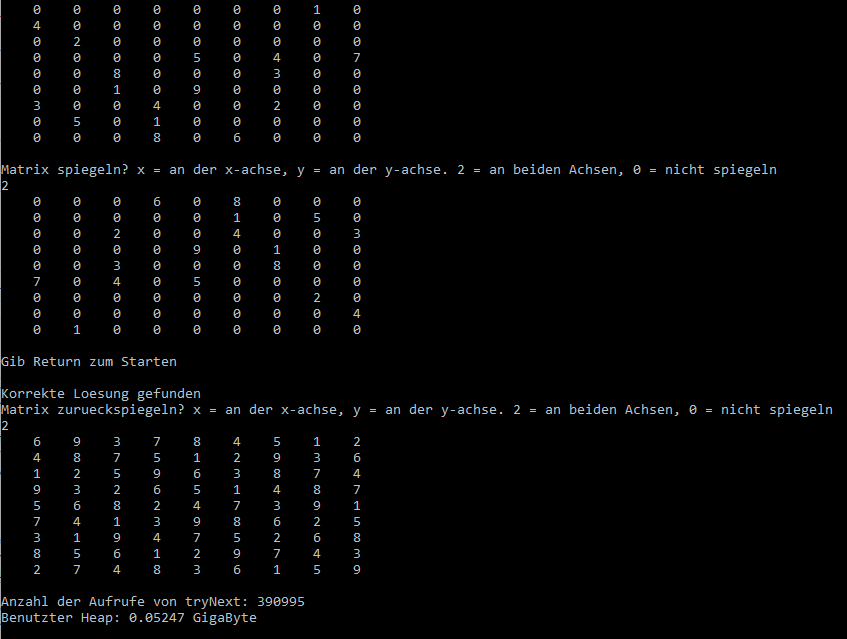
Diese Ergebnisse deuten an, in welche Richtung man eine Optimierung des Programmes machen könnte. So ist es denkbar, die Zeilen so umzusortieren, dass die mit den meisten Vorgabezahlen oben stehen; dabei muss man aber darauf achten, dass die Elementarquadrate nicht durcheinander kommen.
Zum Abschluss noch ein Beispiel für ein 4er Sudoku, die Vorgabezahlen stammen aus [43].
Beispiel 7: (4er Sudoku)
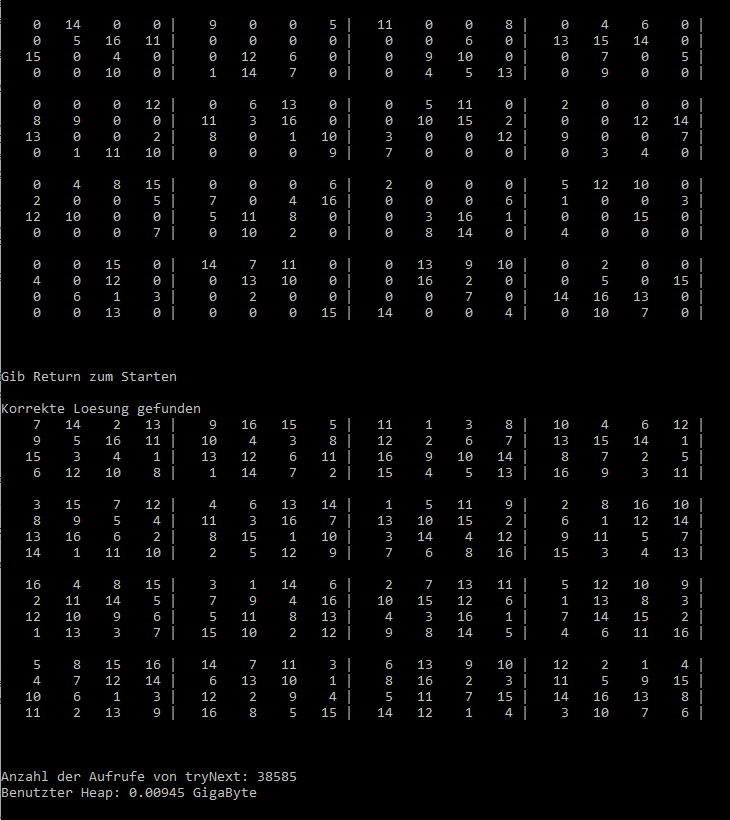
Wer Sudokus lösen möchte, bitte:
Sudoku.exe
Damit verabschiede ich mich für diesmal beim interessierten und ausdauernden Leser in der Hoffnung, dass es gefallen hat.
Literaturverzeichnis
[2] - https://www.math.uni-sb.de/ag/gekeler/LEHRE/KombiSS14/SkriptKombi1112.pdf
[3] - http://www.oemg.ac.at/Mathe-Brief/fba2016/VWA_Hochfilzer.pdf
[4] - https://studyflix.de/elektrotechnik/maschenstromverfahren-329
[5] - https://studyflix.de/elektrotechnik/kirchhoffsche-gesetze-327
[6] - https://de.wikipedia.org/wiki/Netzwerkanalyse_(Elektrotechnik)
[7] - https://studyflix.de/elektrotechnik/linear-unabhangige-maschen-337
[8] - https://mathepedia.de/Wege,_Pfade,_Zyklen_und_Kreise.html
[9] - https://mathepedia.de/Teilgraphen_und_Minoren.html
[10] - https://de.wikipedia.org/wiki/Eulerkreisproblem
[11] - https://de.wikipedia.org/wiki/Hamiltonkreisproblem
[12] - https://thescipub.com/pdf/jcssp.2013.377.382.pdf
[13] - https://matheplanet.com/default3.html?call=viewtopic.php?topic=83447&ref=https%3A%2F%2Fwww.google.com%2F
[14] - https://www.wikiwand.com/de/Adjazenzmatrix
[15] - https://www.spektrum.de/lexikon/mathematik/eigenwert-eines-graphen/2533
[16] - Kenneth M. Hall: An r-Dimensional Quadratic Placement Algorithm, Management Science 1970
[17] - Y. Koren: Drawing Graphs by Eigenvectors: Theory and Practice, AT&T Labs-Research (2003)
[18] - https://www.wikiwand.com/de/Inzidenzmatrix
[19] - https://www.wikiwand.com/de/Laplace-Matrix
[20] - Armin P. Barth, Die Bändigung der Unendlichkeit, Edition ZEITBLENDE
[21] - https://scienceblogs.de/mathlog/2017/11/23/mit-analysis-und-topologie-zum-vierfarbensatz/
[22] - https://www.spektrum.de/lexikon/mathematik/chromatisches-polynom/2355
[23] - https://de.wikiversity.org/wiki/Kurs:Diskrete_Mathematik_(Osnabr%C3%BCck_2020)/Vorlesung_24
[24] - https://de.wikipedia.org/wiki/Baum_(Graphentheorie)
[25] - http://www2.inf.h-brs.de/~pbecke2m/graphentheorie/
[26] - https://de.wikipedia.org/wiki/Zyklus_(Graphentheorie)
[27] - https://de.wikipedia.org/wiki/Union-Find-Struktur
[28] - https://algorithms.discrete.ma.tum.de/graph-algorithms/flow-ford-fulkerson/index_en.html
[29] - http://www-home.htwg-konstanz.de/~bittel/ain_alda/Vorlesung/10_Graphen_Fluesse.pdf
[30] - https://graphonline.ru/de/
[31] - https://de.wikipedia.org/wiki/Max-Flow-Min-Cut-Theorem
[32] - https://www.youtube.com/watch?v=8sODtF2Fk_E
[33] - https://de.universaldenker.org/illustrationen/917
[34] - https://www.mathe2.uni-bayreuth.de/stoll/teaching/EinfAlg-SS2018/Skript-EinfAlg-pub-print.pdf
[35] - https://imsc.uni-graz.at/baur/lehre/SS2018/11-Seebacher.pdf
[36] - https://de.wikipedia.org/wiki/Sudoku#Die_Mathematik_hinter_Sudoku
[37] - https://www.sueddeutsche.de/wissen/sudoku-die-suche-nach-der-kniffligsten-kombination-1.912970-0
[38] - https://www.math.uni-bielefeld.de/~dotten/files/schulbesuche/Schulbesuch20141024.pdf
[39] - https://www.zib.de/berthold/sudoku.pdf
[40] - https://matheplanet.com/default3.html?call=viewtopic.php?topic=205911&ref=https%3A%2F%2Fwww.google.com%2F
[41] - Walter Klotz, Torsten Sander: Wie kommt Sudoku zu ganzzahligen Eigenwerten?, Math. Semesterberichten (2010) 57, 169 - 183
[42] - N. Wirth, Algorithmen und Datenstrukturen, Teubner Studienbücher Infromatik
[43] - https://de.wikipedia.org/wiki/Sudoku
[44] - F.Kaderali, W. Poguntke, Graphen, Algorithmen und Netze