- 1 Vorwort
- 2 Das kleine h
- 3 Die kontinuierliche logistische Gleichung
- 4 Die Diskretisierung der kontinuierlichen logistischen Gleichung
- 5 Transformation zur logistischen Gleichung
- 6 Das deterministische Chaos
- 6.1 Das Feigenbaumdiagramm
- 6.2 Kenngrößen des Feigenbaumdiagramms
- 6.3 Der Lyapunov-Exponent.
- 6.4 Fenster auf, Fenster zu: ich krieg die Krise
- 6.5 Das Genie beherrscht das (deterministische) Chaos
- 6.6 Feigenbaum und Mandelbrot
- 7 Literaturverzeichnis und anderes
Die Suche nach dem kleinen h
Vorwort
Der Inhalt dieses Aufsatzes ist weit über das geplante Volumen hinaus gegangen. Ursprünglich wollte ich nur meinen Unmut über die Schlampigkeit, die zum Verlust des "kleinen h" geführt hat, Ausdruck verleihen. Aber die Faszination des sich daraus eröffnenden, für mich größtenteils neuen Teilgebietes meiner Passion Mathematik, der Chaostheorie, hat mich nicht losgelassen. Und so bin ich immer tiefer in die Materie eingetaucht, immer neue, verblüffende, wunderbare Eigenschaften und Methoden kennenlernend.
Die Erarbeitung hat mich geraume Zeit beschäftigt, einen Teil davon habe ich während einer längeren Krankheit durchgeführt, die mich zwar vom Arbeitsleben und vielen anderen schönen Dingen des Lebens abgehalten hat, aber zum Glück nicht am Denken hinderte.
So habe ich durch das "deterministische Chaos" etwas Ordnung in mein Chaos gebracht; ich hoffe, man merkt mir die Begeisterung an - und sie überträgt sich!
Das kleine h
$\mathtt{\lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}}$
Und weil das h so (haar-)klein ist, also so nahe bei Null, wird es schon mal gerne übersehen, zumindest hatte ich diesen Eindruck, als ich mich vor einiger Zeit mit einigen Artikel aus dem Internet über die so genannte "Logistische Gleichung" beschäftigt habe.
Als logistische Gleichung wird eine Differenzengleichung bezeichnet, die das Wachstum (oder die Schrumpfung) unterschiedlicher Entitäten beschreiben soll (z.B. in der Biologie, Physik oder in den Wirtschaftswissenschaften). Sie lautet:
$\mathtt{b_{n+1}= \lambda b_n (1-b_n) \text{ (*)}}$
Als ich die Gleichung in einem populärwissenschaftlichen Buch über "Chaostheorie" (Joachim Bublath: Chaos im Universum, Kapitel 10 [9]) zum ersten mal sah, fragte ich mich schon, ob es zu dieser Differenzengleichung eine kontinuierliche Variante in Form einer Differentialgleichung gibt (was nicht unbedingt sein muss) und vor allem, wo denn die Zeit in dieser Gleichung geblieben war. Ich kannte Wachstumsgleichungen in Form von Differentialgleichungen, die natürlich zeitabhängig sind, also deren unabhängige Variable die Zeit ist.
Aber gut, auch die Fibonacci-Zahlen sollen ja eine Aussage über die Vermehrung von Kaninchen machen und enthalten auch keinen expliziten Zeitfaktor.
Der zweite interessante Aspekt war der Zusammenhang zum so bezeichneten chaotischen Verhalten, was immer man darunter versteht. (Über dieses Thema und den Zusammenhang zu obiger Gleichung mehr im zweiten Teil des Aufsatzes)
Ein zweites Mal begegnete ich der logistischen Gleichung in einer Facharbeit eines Schülers [6], geschrieben an einem bayerischen Gymnasium im Leistungskurs Mathematik (Hut ab, die Arbeit hat mir gut gefallen). Dort wurde der Zeitfaktor mit 1 Jahr (sicherlich beispielhaft) angegeben und das Chaos in das die Iteration der Gleichung bei bestimmten Werten für $\mathtt{\lambda}$ führt, als "deterministisches Chaos" bezeichnet.
An mehreren anderen Stellen wiederum, wird gesagt, die logistische Gleichung wäre durch das Eulerverfahren aus einer kontinuierlichen Differentialgleichung herleitbar. Aha! Aber dann müsste ja irgendwo auch die Zeit auftauchen, die in der kontinuierlichen Gleichung ja nun einmal vorkommt. Wo ist sie geblieben?
Schauen wir also mal in die diesbezügliche Mathematik und gehen auf die Suche. Damit das Ganze ins Kapitel über Visualisierungen passt, will ich alles reich bebildern. Wie immer werden die Herleitungen in eigenen Dokumenten hinterlegt, für die, die wissen wollen, wie es im Detail aussieht.
Die kontinuierliche logistische Gleichung
Sei
$\mathtt{B: [0,\infty] \rightarrow [0, \infty]} \\ \mathtt{t \rightarrow B(t)\quad B'(t) = rB(t)(M-B(t))}$
Die Differentialgleichung wird zur Anfangswertaufgabe, wenn man die Anfangsbedingung B(0) = B0 hinzunimmt, wobei B0 aus dem Intervall [0, M] stammt.
Die logistische Wachstumsgleichung simuliert das Wachstum einer Entität anders als das exponentielle Wachstum $\mathtt{(B'(t) = rB(t))}$ durch Beschränkung des Wachstums mittels des Faktors (M-B(t)) und gibt so ein realistischeres Bild des Wachstumsverhaltens. Wie wir an den Lösungsgrafiken sehen werden, ist der Begriff Kapazitätsgrenze für M gut motiviert.
Die Anfangswerte für B(t) zur Zeit t=0, 0 und M, liefern zwei konstante Lösungen, nämlich B = 0 und B = M.
Die Lösung der Differentialgleichung gelingt mit Hilfe der "Trennung der Variablen".
$\mathtt{B(t) = \frac{B_0 M}{B_0 + (M - B_0) \exp(-rMt)}}$
Die folgenden Grafiken zeigen den Verlauf der Funktion B(t) für verschiedene Parameter r, M und B0:

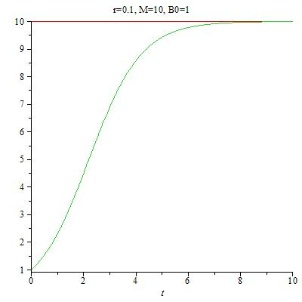

Für r > 0 (Wachstum) nähert sich B(t) asymptotisch dem Wert von M. Das Wachstum beginnt zunächst exponentiell und wird dann durch den begrenzenden Faktor M-B(t) abgebremst.
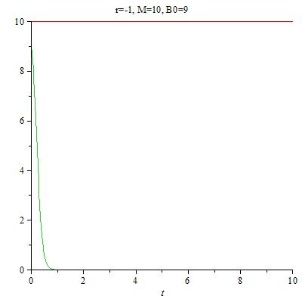
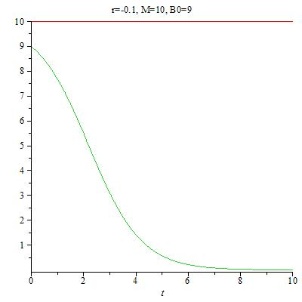
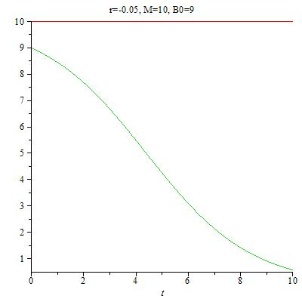
Für r < 0 (Schrumpfung) nähert sich B(t) asymptotisch dem Wert 0 an.
Der Wert r = 0 liefert eine konstante Gerade in Höhe B0.
Mathematische Herleitungen zur kontinuierlichen logistischen Differentialgleichung.
Die Diskretisierung der kontinuierlichen logistischen Gleichung
Wie sieht das bei unserer Anfangswertaufgabe aus? (Natürlich ist ein solches Vorgehen bei unserer Anfangswertaufgabe überflüssig, es gibt ja eine geschlossene Darstellung der Lösung, aber es ist auch mal interessant, zu untersuchen, wie sich eine Näherungslösung verhält, in direktem Vergleich zur korrekten Lösung.)
Zunächst ist der x-Wert hier die Zeit, wir schreiben also statt x als unabhängiger Variable t.
B'(t) wird "diskretisiert", also durch $\mathtt{\frac{B(t+h) - B(t)}{h}}$ ersetzt. Dabei stellt h hier ein Zeitintervall zwischen zwei Berechnungzeiten tn und tn+1 dar (h = tn+1 - tn ), das oft als ∆t, mit dem griechischen Buchstaben ∆, bezeichnet wird. Wir bleiben aber hier bei unserem kleinen h.
Durch Einsetzen und Umformen in die Differentialgleichung ergibt sich:
$\mathtt{B_{n+1} = B_n + h r B_n (M - B_n) \text{ (**)}}$
Bei der Berechnung beginnt man nun also mit dem Startwert zur Zeit t0 = 0, d.h. man setzt B0 in die Gleichung (**) ein und berechnet daraus B1. Doch halt, da fehlt ja noch das kleine h! Wie wählt man das nun? Ja eben, klein. An dieser Stelle wäre nun ein ziemlicher Apparat der numerischen Mathematik zu bemühen, der die Voraussetzungen schafft, um etwas über die Konvergenzeigenschaften der Differenzengleichung bzw. die Güte der daraus zu berechnenden Näherung auszusagen. Das sparen wir uns und sagen einfach so: je kleiner h, desdo besser die Näherung der Bn an die B(tn ). Aber auch: je kleiner h, desdo aufwändiger die Rechnung. Um einen Eindruck von der Abhängigkeit der Güte der Näherungslösung zu erhalten soll uns hier lediglich eine Veranschaulichung durch mehrere Grafiken ausreichen. Im Anhang werden Gütekriterien für numerische Verfahren vorgestellt und kurz erläutert.
Um eine solche Berechnung in einem Programm durchzuführen, habe ich nicht das von mir so geliebte Pascal verwendet, sondern wegen der grafischen Möglichkeiten Maple vorgezogen. Die folgenden Grafiken enthalten immer auch die (korrekte) kontinuierliche Lösung in grüner Farbe und variieren den Wert für h. Die Punkte (tn , Bn) sind durch Strecken verbunden um einen kontinuierlichen Verlauf der Näherungslösung zu suggerieren (in roter Farbe).
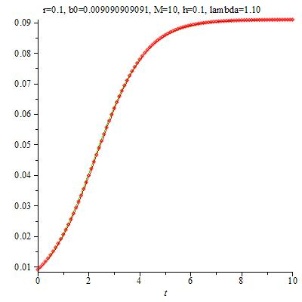
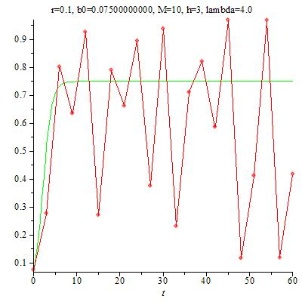
Das Beispiel r=0.1, B0=1, M=10 wurde mit verschiedenen Werten für h gerechnet mit folgenden Ergebnissen:
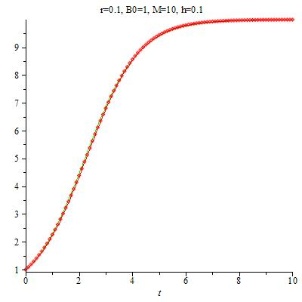
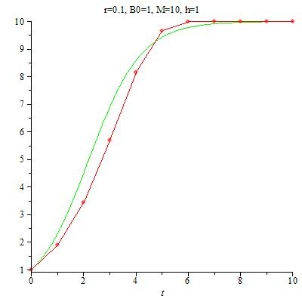
Im ersten Bild, h = 0.1, stimmt die rote Näherungslösung mit der grünen kontinuierlichen Lösung sehr gut überein. Wählt man h nun größer (h=1), dann weicht die Näherung deutlich von der kontinuierlichen Lösung ab, liegt aber noch in ihrer Nähe. Schauen wir, was geschieht, wenn wir h weiter vergrößern:
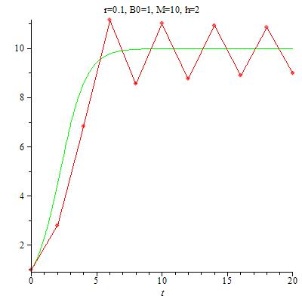

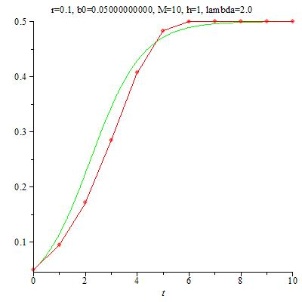
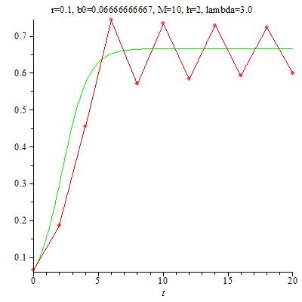
Für h=2 ist zwar noch eine Tendenz entlang der kontinuierlichen Lösung erkennbar, bei h=3 haben die berechneten Werte augenscheinlich überhaupt nichts mehr mit der kontinuierlichen Lösung zu tun.
Klar, wenn h so groß ist ...
Gar nichts ist klar! Das folgende Bild zeigt ein ähnlich krauses Verhalten für h = 0.01 (bei anderen Parametern für r und M):
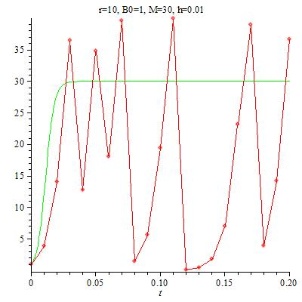
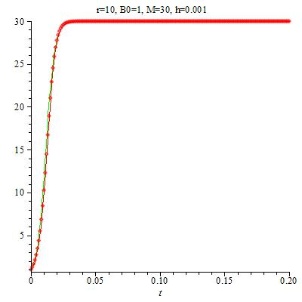
Also keine voreiligen Schlüsse, bitte! Wie die zweite Grafik zeigt, kann man auch hier durch noch kleineres h eine vernünftige Näherungslösung finden.
Eine Fehlerabschätzung zwischen kontinuierlicher und diskreter Lösung findet sich beispielsweise in der Arbeit "Numerische Verfahren für Differentialgleichungen" von Steffen Börm [8] in Lemma 3.1. Zusammen mit der Abschätzung der zweiten Ableitung aus dem letzten Kapitel kann man abschätzen:
$\mathtt{|B(h) - B_1| \le \frac{h^2}{2} r^2 \frac{M^3}{4} = \frac{r^2 M^3}{8}h^2}$
| h | max. Fehler |
| 0.1 | 0.0125 |
| 1 | 1.25 |
| 2 | 5 |
| 3 | 11.25 |
Bei r=10 und M=30 im zweiten Beispiel ergibt sich:
| h |
max. Fehler |
| 0.001 |
0.3375 |
| 0.01 |
33.75 |
Gütekriterien numerischer Verfahren
An dieser Stelle könnte man zufrieden sein mit den bisherigen Ergebnissen, wenn, ja wenn es nicht die anfangs aufgeschriebene Gleichung (*) gäbe und man gerne den Zusammenhang zwischen unseren bisherigen Ergebnissen und eben dieser Gleichung wüsste. Damit beschäftigt sich das nächste Kapitel.
Transformation zur logistischen Gleichung
$\mathtt{ T_0 : [0, M] \rightarrow [0,1) }$
$\mathtt{x \rightarrow \frac{r h x}{1 + r h M}}$
Dies ist eine Geradengleichung mit der Steigung $\mathtt{s=\frac{r h}{1 + r h M}}$. Für positives r ist auch s positiv.
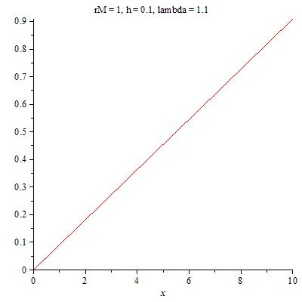
Skizze der Funktion T0(x).
Setzt man nun bn := T0 (Bn ) und ebenso für n+1, dann wird aus der Gleichung (**) die Gleichung (*), wobei $\mathtt{\lambda := 1 + r h M}$ gewählt werden muss. Wenn die in der logistischen Gleichung vorausgesetzte Beschränkung $\mathtt{\lambda \le 4}$ hinzugenommen wird, dann muss $\mathtt{h \le \frac{3}{r M}}$ sein.
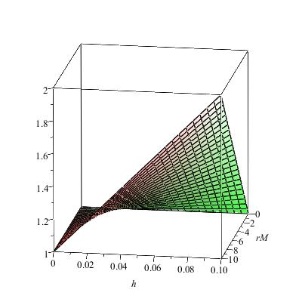
Darstellung des Zusammenhangs $\mathtt{\lambda := 1 + r h M}$. Dabei ist auf einer Abszisse das Produkt aus r und M aufgetragen, auf der anderen h. Auf der Ordinate ist $\mathtt{\lambda}$ aufgetragen.
$\mathtt{ T_1 : [0, M] \rightarrow [0,1)}$
$\mathtt{x \rightarrow \frac{r h (x-M)}{1 - r h M}}$
Dies ist eine Geradengleichung mit der Steigung $\mathtt{s=\frac{r h}{1 - r h M}}$. Für negatives r ist auch s negativ.

Skizze der Funktion T1(x).
Setzt man nun bn := T1 (Bn ) und ebenso für n+1, dann wird aus der Gleichung (**) die Gleichung (*), wobei $\mathtt{\lambda := 1 - r h M}$ gewählt werden muss. Wenn die in der logistischen Gleichung vorausgesetzte Beschränkung $\mathtt{\lambda \le 4}$ hinzugenommen wird, dann muss $\mathtt{h \le -\frac{3}{r M}}$ sein.
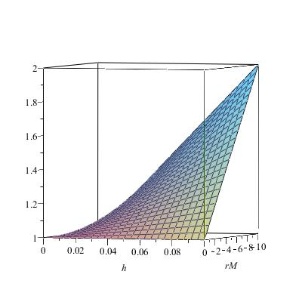
Darstellung des Zusammenhangs $\mathtt{\lambda := 1 - r h M}$. Dabei ist auf einer Abszisse das Produkt aus r und M aufgetragen, auf der anderen h. Auf der Ordinate ist $\mathtt{\lambda}$ aufgetragen.
$\mathtt{b_{n+1} = \lambda b_n (1 - b_n) \text{ mit } 0 \le b_0 \le 1 \text{ und } 1 < \lambda \le 4}$
$\mathtt{b_{n+1}=(1+|r| h M) b_n (1 - b_n) \text{ mit}}$
$\mathtt{0 \le b_0 \le 1 \text{ und}}$
$\mathtt{0 < h \le \frac{3}{|r| M}}$
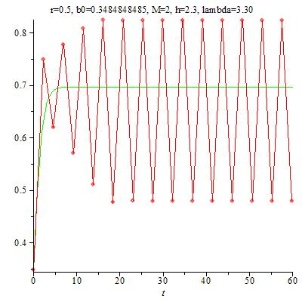
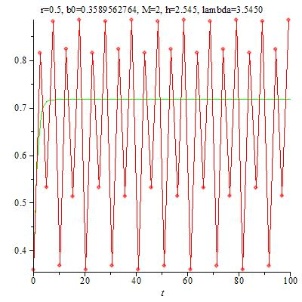
Irgendwie kommen einem die Grafiken bekannt vor. Kein Wunder, sie entsprechen den Grafiken in den Abbildungen 7 bis 10 im Kapitel über Diskretisierungen, bis auf die Werte auf der senkrechten Achse, auf der hier die bn, dort die Bn, aufgetragen sind. Auch das ist kein Wunder, schließlich sind die bn aus den Bn durch die lineare Transformation T0 hervorgegangen (bn = T0(Bn)). Letztlich steuert (bei festgehaltenem r und M und transformiertem b0 = T0(B0)) allein die Diskretisierungsfeinheit h die Konvergenz und damit das Aussehen des Graphen. Damit steckt der Zeitparameter, eben h, weiterhin in der logistischen Gleichung, er wird nur durch das als Abkürzung eingeführte $\mathtt{\lambda \quad (=1 + r h M)}$ verschleiert.
Was hätte man auch anderes erwarten können?
Ich habe, natürlich ohne Anspruch auf Vollständigkeit, keinen Aufsatz im Internet gefunden, wo diese Tatsache auch nur bemerkt würde. Selbst in Arbeiten, wo immerhin die lineare Transformation der diskretisierten Gleichung in die logistische Gleichung vorgestellt wurde, verschwindet h sang- und klanglos ohne jede Erwähnung in $\mathtt{\lambda}$ - es versinkt praktisch im Chaos.
Somit ist die Betrachtung der logistischen Gleichung in Abhängigkeit von $\mathtt{\lambda}$ zunächst nichts anderes als die Untersuchung des Konvergenzverhaltens des Eulerverfahrens angewendet auf die kontinuierliche Wachstumsgleichung. Von diesem Blickwinkel aus, ist eigentlich die einzig interessante Frage, bis zu welchem h die Diskretisierung noch konvergiert, soll heißen gute Näherungswerte liefert.
Darüber hinaus wird in ebenso vielen Beiträgen als Entdecker der logistischen Gleichung der belgische Mathematiker Pierre-Francois Verhulst (1804 - 1849) genannt. Er hat sich mit der Untersuchung von Bevölkerungswachstum seines Heimatlandes und anderer Länder beschäftigt und die kontinuierliche logistische Gleichung für diese Zwecke verwendet (was auch sonst, die Lösung ist ja geschlossen darstellbar). Verhulst hat tatsächlich den "bremsenden Term" (M-B(t)) in die vorher rein exponentielle Gleichung eingeführt und kam damit der Realität des Bevölkerungswachstums sehr nahe. Aber in seiner Arbeit von 1845 benutzt er nur die kontinuierliche Gleichung, die er weder diskretisiert noch transformiert hat (siehe dazu beispielsweise diesen Auszug aus seiner Arbeit in deutscher Übersetzung), ebenso wenig wie in seiner Veröffentlichung von 1938.
Ich will aber die in anderer Richtung erzielten weitreichenden Ergebnissen der Untersuchung der logistischen Gleichung vieler Anderer nicht klein reden. Die Verselbständigung der logistischen Gleichung in Richtung der Chaostheorie trägt interessante, ja spannende Züge, über die ich im letzten Kapitel berichten werde.
Hier ist aber noch einiges aufzuarbeiten, zunächst einmal die Konvergenzaussagen der logistischen Gleichung für verschiedene $\mathtt{\lambda}$. Dabei handelt es sich aber um Konvergenzaussagen für die Folge {bn} gegen einen Grenzwert g der reellen Zahlen. Die Frage, ob bzw. wie gut die durch Diskretisierung der Differentialgleichung berechnete Näherungslösung die kontinuierliche Lösung approximiert, hat damit (und somit mit $\mathtt{\lambda}$) nur mittelbar zu tun, wie man gut an Abbildung 19 erkennt: zwar konvergieren die bn gegen den y-Wert der Asymptote der kontinuierlichen Lösung, aber als Näherungslösung für die Anfangswertaufgabe sind sie unbrauchbar! Es sei schon hier klar gesagt, dass die Frage, ob die bn konvergieren oder wie sie sich sonst für $\mathtt{n \rightarrow \infty}$ verhalten, für die Aufgabenstellung der kontinuierlichen Wachstumsgleichung ohne Belang ist - wer kann schon unendlich lange warten.
| Nr |
lambda-Intervall | Verhalten |
Abb. |
| 0 | [0, 1] | konvergiert bn gegen 0 | |
| 1 |
]1, 2] | konvergiert bn monoton gegen $\mathtt{\frac{\lambda - 1}{\lambda}}$ | 18 |
| 2 |
]2, 3] | konvergiert bn alternierend gegen $\mathtt{\frac{\lambda - 1}{\lambda}}$ | 19 |
| 3 | $]3,\quad 1 + \sqrt{6}=3,4494...[$ | hat bn zwei Häufungspunkte (bei fast allen Startwerten) | 21 |
| 4 | $]1 + \sqrt{6}, \quad 3,5440...[$ | hat bn vier Häufungspunkte (bei fast allen Startwerten) | 22 |
| 5 | ]3,5440..., 3,5699...[ | hat bn 8, 16, 32, ... Häufungspunkte | 23 |
| 6 | ]3,5699..., 4[ | keine Konvergenz, keine Häufungspunkte (mit Ausnahme bestimmter $\mathtt{\lambda}$-Fenster) | 20 |
| 7 | > 4 | Divergenz außerhalb [0, 1] | 24 |
Konvergenztabelle für $\mathtt{\lambda}$
Der Grenzwert $\mathtt{\frac{\lambda - 1}{\lambda}}$ ist natürlich nichts anderes als der transformierte Grenzwert M der kontinuierlichen Lösung der logistischen Gleichung für r > 0, also T0(M) = $\mathtt{\frac{\lambda - 1}{\lambda}}$ und des Grenzwertes 0 für r < 0, also T1(0) = $\mathtt{\frac{\lambda - 1}{\lambda}}$.

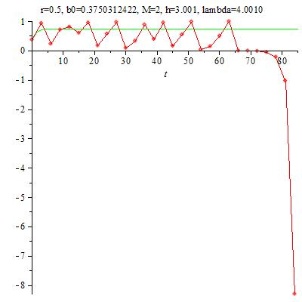
Die obigen Ergebnisse über $\mathtt{\lambda}$ finden sich mit Herleitung in verschiedensten Aufsätzen, z.B. einer zweiten Facharbeit aus 1998 [7] oder bei Wikipedia.
Der Fall r < 0 mit der Transformation T1, die Bn in bn umsetzt, zeitigt entsprechende Ergebnisse, wobei aufgrund der negativen Steigung von T1 eine Spiegelung der bn - Werte erfolgt.
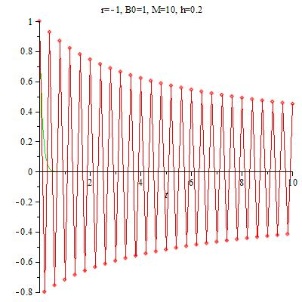

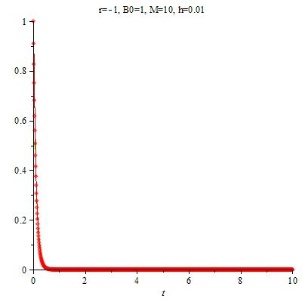
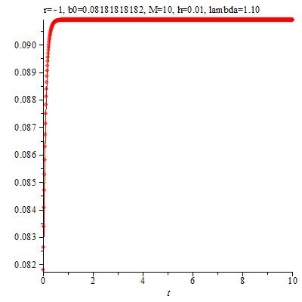
Den $\mathtt{\lambda}$ - Werten zwischen 0 und 1 entspricht keine Transformation aus der diskretisierten Gleichung; für diese $\mathtt{\lambda}$ konvergiert die Folge der bn gegen Null.
Auch die Frage nach expliziten Lösungen der logistischen Gleichung soll hier noch beantwortet werde. Für $\mathtt{\lambda}$ = 2 und $\mathtt{\lambda}$ = 4 existieren solche Lösungen.
Für $\mathtt{\lambda}$ = 2 löst
$\mathtt{b_n := \frac{1}{2} - \frac{1}{2} (1-2b_0)^m \text{ mit }m=2^n}$
die logistische Gleichung.Für $\mathtt{\lambda}$ = 4 ist es
$\mathtt{b_n := \frac{1}{2} (1- \cos(2n 2p y_0)) \text{ mit } y_0 := \frac{1}{2n} \arccos(1 - 2b_0)}$
siehe Schuster [2], Seite 59f.Die Transformation der diskretisierten logistischen Gleichung
Das deterministische Chaos
Dieses und die folgenden Kapitel enthalten einige Ergebnisse der Untersuchungen der logistischen Gleichung (teilweise) ohne weitere Herleitung; diese finden sich in vielen Veröffentlichungen im Internet. In den Anhängen habe ich allerdings einige Beweise und Beweisideen skizziert. Mir kommt es darauf an, die (mathematische) Ordnung im Chaos darzustellen.
Die mathematischen Begriffe, die im Zusammenhang mit der Chaostheorie stehen, haben, wie wir sehen werden, eine ebenso exakte Grundlage wie andere mathematische Definitionen, sonst wäre es ja auch keine Mathematik. Ich will versuchen, da die Begriffsbildungen im Allgemeinen nicht zu den in der Oberstufe oder den Erstsemestern eingeführten gehört, darzustellen, welcher rote Faden sich in diesem Teil der Mathematik erkennen lässt. Im folgenden werde ich die Abschnitte, die sich auf das konkrete Beispiel, die logistische Gleichung, beziehen, kursiv darstellen.
Völlig fern aller klassischen Didaktik beginne ich mal mit einer lockeren Aufzählung der Vokabeln, die in diesem Zusammenhang verwendet werden:
- Orbit eines Iterationsverfahrens
- Attraktor
- Repeller
- n-periodischer Punkt, Zyklus
- Periodenverdopplung
- Feigenbaumdiagramm
- sensitive Abhängigkeit von den Anfangswerten
- Lyapunov-Exponent
- Bifurkation
- Feigenbaumkonstanten
- Akkumulationspunkt, Feigenbaumpunkt
- fraktale Menge
- Selbstähnlichkeit
- Skaleninvarianz
- Intermittenz
- laminare Phase
- Tangentenbifurkation
- Fenster
- sensitive Abhängigkeit von Parametern
- deterministisches Chaos
Unsere logistische Gleichung (*) schreiben wir unter Verwendung einer Funktion g(x) = $\mathtt{\lambda}$ x(1 - x) auf dem Intervall [0,1], sodass sich das Iterationsverfahren als bn+1 = g(bn) schreibt mit Startwert b0. Es sei ausdrücklich darauf hingewiesen, dass g immer auch von $\mathtt{\lambda}$ abhängt! Wir betrachten zunächst $\mathtt{\lambda}$ als Parameter, beliebig aber fest, ohne ihn als Subskript oder Argument anzuschreiben.
Leitfaden für die weiteren Überlegungen ist zunächst die Konvergenztabelle aus dem letzten Abschnitt.
Die Werte (bi) nennt man auch den Orbit (1) von g in Bezug auf den Startwert b0. Für immer größer werdendes n und unter der Voraussetzung der Konvergenz der bn gegen einen Grenzwert b wird die Differenz aufeinanderfolgender bi, also |bi+1 - bi| immer geringer, da eine konvergente Folge auch immer eine Cauchyfolge ist. Somit gilt für den Grenzwert b die Beziehung b = g(b). Man nennt b einen Fixpunkt von g.
Der Banachsche Fixpunktsatz macht eine positive Aussage über die Existenz und Eindeutigkeit eines Fixpunktes x* = f(x*) einer Funktion f auf einem abgeschlossenen Intervall [a, b], die eine Lipschitzbedingung mit einer Konstante $\mathtt{0 \le L < 1}$ erfüllt
$\mathtt{|f(x) - f(y)| \le L|x - y|}$
(kontrahierende Abbildung). Eine Funktion die stetig differenzierbar ist, erfüllt eine solche Lipschitzbedingung, wenn ihre Ableitung auf [a, b] betraglich kleiner 1 ist: |f'(x)| < 1. Der Fixpunktsatz sagt auch, dass unter dieser Voraussetzung die Iteration xn+1 = f(xn) für jeden Startwert x0 aus [a, b] gegen x* konvergiert.
Wenn ein Fixpunkt existiert, so heißt dies andererseits aber nicht, dass f kontrahierend sein muss.
Dieser Satz motiviert nun folgende
Definition 1:
a) Der Fixpunkt x* einer stetig differenzierbaren Funktion f heißt Attraktor (2) (oder wird "stabil" genannt), wenn |f'(x*)| < 1.b) Der Fixpunkt x* einer stetig differenzierbaren Funktion f heißt Repeller (3) (oder wird "instabil" genannt), wenn |f'(x*)| > 1.
c) Der Fixpunkt x* einer stetig differenzierbaren Funktion f wird "superstabil" genannt, wenn |f'(x*)| = 0.
d) Der Punkt x* einer stetig differenzierbaren Funktion f wird "indifferent" genannt, wenn |f'(x*)| = 1.
Visualisieren, visualisieren ... klar:
Wir zeichnen f und die 1. Winkelhalbierende in ein Koordinatensystem ein und betrachten die Umgebung des Schnittpunktes der beiden Graphen (den muss es geben, wenn ein stetiges f ein Intervall auf sich selber abbildet):
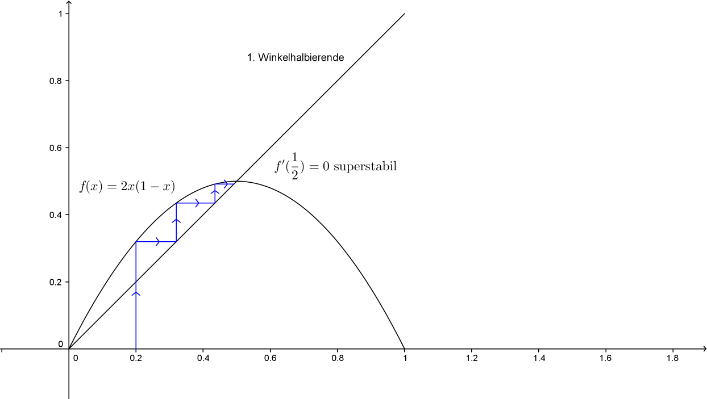

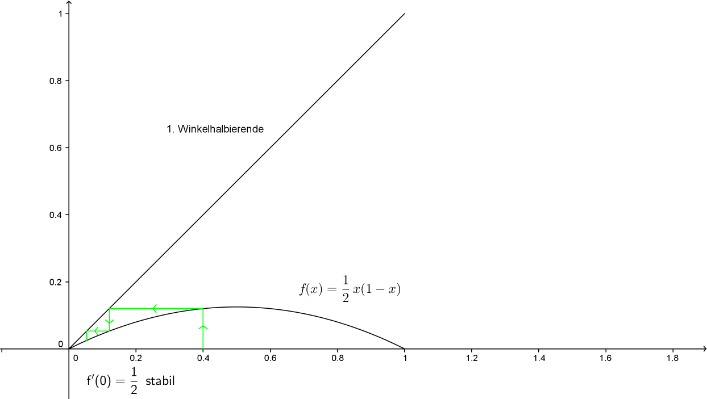
Das Iterationsverfahren, genauer seinen Orbit, kann man graphisch bestimmen und einzeichnen, indem man vom Startwert x0 aus senkrecht auf die Funktion stößt und dann waagrecht zur Winkelhalbierenden geht: man erhält x1 als x-Wert des Treffpunktes und dann wieder senkrecht auf die Funktion, waagrecht auf die Winkelhalbierende und so weiter ...
Leicht erkennt man, wieso die Namen Attraktor und Repeller gerechtfertigt sind. (Man kann durchaus die Definition von Attraktor und Repeller zunächst elementarer formulieren und dann die obigen Definitionen als Satz beweisen, siehe z.B. [1], [3])
Weitere theoretische Aussagen habe ich in dem Anhang
Theoretische Ergebnisse zur n-Periodizität und Attraktion
zusammengestellt.
Unser logistisches Beispiel g hat zwei Fixpunkte: $\mathit{b = g(b)\Leftrightarrow b = \lambda b(1 - b) \Leftrightarrow b = 0 \textit{ oder } b = \frac{\lambda - 1}{\lambda}}$. Die Betrachtung der ersten Ableitung von g zeigt:
g'(x) = $\mathtt{\lambda}$ (1 - 2x)
g'(0) = $\mathtt{\lambda}$ liefert nach Banach Konvergenz für $\mathtt{\lambda}$ - Werte zwischen $\mathit{0 \le \lambda < 1}$, für $\mathtt{\lambda}$ = 1 haben wir in Null einen indifferenten Fixpunkt, aber auch hier konvergiert die Iteration gegen 0; für $\mathtt{\lambda}$ = 0 ist Null superstabil. (Fall 0 in obiger Konvergenztabelle)
$\mathit{g'(\frac{\lambda - 1}{\lambda}) = 2-\lambda}$
Wie unsere Beispiele aus den bisherigen Kapiteln zeigen, beginnt jenseits des Konvergenzbereiches (für $\mathtt{\lambda}$) nicht sofort die Divergenz (im Sinne eines Verlassens des Intervalls [0, 1], Fall 7), sondern man kann sich vorstellen, das die Konvergenz gegen einen Grenzwert aufgeweicht wird und zunächst in mehrere Häufungspunkte "zerfließt". Als weitere Eigenschaft von Punkten des Orbit betrachten wir daher deren Periodizität unter Anwendung von f auf die Orbitwerte.
Definition 2:
$\mathit{g^2(x^\circ) = g(g(x^\circ)) = x^\circ \Leftrightarrow}$
$\mathit{x^\circ = 0 \textit{ oder } x^\circ = \frac{\lambda - 1}{\lambda}}$
oder
$\mathit{x^\circ = \frac{1 + \lambda + \sqrt{\lambda^2 - 2*\lambda - 3}}{2 * \lambda}}$ (#)
oder
$\mathit{x^\circ = \frac{1 + \lambda - \sqrt{\lambda^2 - 2*\lambda - 3}}{2 * \lambda}}$ (##)
.
.
Es gibt auch bei n-periodischen Punkten (n >= 1) Attraktor- und Repellereigenschaften, die sich in einer entsprechenden Definition 3 festlegen lassen:
Man sagt, ein n-Zyklus hat die Attraktoreigenschaft (oder ist stabil), wenn |(fn)'(x)| < 1 bzw. die Repellereigenschaft (oder ist instabil), wenn |(fn)'(x)| > 1 für alle x des n-Zyklus ist, wir nennen ihn einen Superzyklus, wenn die erste Ableitung für alle x Null ist.
Die einzelnen xi des n-Zyklus sind wie schon gesagt Fixpunkte von fn.
Um dies nochmals deutlich zu machen: Die Folgen (bn) nähern sich den n-periodischen Punkten (n auch = 1, also bei Fixpunkten) im Allgemeinen immer mehr an, sie erreichen sie aber nicht, es sei denn, ein solcher Punkt wird als Startwert verwendet, auch wenn in Abbildung 32 suggeriert wird, dass die bn die Häufungspunkte exakt treffen! Deshalb muss man auch in der Bezeichnung zwischen der Iterationsfolge (hier (bi), i=0..∞) und den n-periodischen Punkten (x0, x1, x2, ..., xn-1) eines Zyklus fein unterscheiden.
Die Definition des n-Zyklus hat die Berechnung der Häufungspunkte ermöglicht, aber wir wissen noch nicht, wie man die $\mathtt{\lambda}$ - Werte ermittelt, für die die Häufungspunkte vorliegen. Dies lässt sich nun aus der Definition 3, der n-Zyklus Attraktoreigenschaft herleiten.
|(g(g(x)))' | < 1 benutzt die Kettenregel um die Beziehung $\mathit{|\lambda^2 + \lambda + 4| < 1}$ zu erhalten, wenn man die oben berechneten Werte für die 2-periodischen Punkte (#) und (##) einsetzt; es ergibt sich dann für positive $\mathtt{\lambda}$:
$\mathit{3 < \lambda < 1 + \sqrt{6}}$
also eben die Beziehung aus der Konvergenztabelle, Fall 3.
Fassen wir nochmal zusammen: Zwei Gleichungen bestimmen das Verhalten bzgl. n-Periodizität und den Attraktionseigenschaften:
fn(x°) = x° für die n-Periodizität und
|(fn)'(x°)| < 1 für die Attraktoreigenschaft.
Man könnte nun auf die Idee kommen, weitere Berechnungen für höhere Periodizitäten als 2 durchzuführen. Dies habe ich in der folgenden Anlage auch mal gemacht, allerdings, schon hier verraten, ist g4 bereits ein Polynom 16-ten Grades und die Nullstellen von g4(x) - x sind nicht mehr geschlossen berechenbar, ebenso wenig wie die Abschätzung der ersten Ableitung von g4. Trotzdem ist das Ergebnis nicht uninteressant, insbesondere, wenn man zugehörige grafische Darstellungen betrachtet. Auch die Frage nach einer 3-Periodizität wird dort beantwortet.Ein wichtiges, in der vorherigen Anlage hergeleitetes Ergebnis, stellt eine weitere Tatsache im Zusammenhang mit der Periodizität und Attraktion dar:
Bemerkung:
Für alle Punkte (xi) eines n-Zyklus ist die Steigung von fn gleich, d.h. sie haben alle das gleiche Stabilitätsverhalten in Abhängigkeit von $\mathtt{\lambda}$. Somit hätte man bei der Definition der Attraktor- bzw. Repellereigenschaft eines n-Zyklus die Forderung nur für ein Element des Zyklus stellen müssen.
Praktische Ergebnisse zur n-Periodizität und Attraktion
Zugehörige animierte Grafiken:
log_Dgl_g
log_Dgl_g2
log_Dgl_g3
log_Dgl_g3_0_4
log_Dgl_g4
Letztlich zeigt sich in weiteren theoretischen Betrachtungen, dass die Periodizität mit dem Faktor 2 zunimmt, wobei die dafür zulässigen $\mathtt{\lambda}$-Intervalle immer kleiner werden (siehe Konvergenztabelle Fall 5). Man spricht hier von einer sog. Periodenverdopplung (5).Folgende Tabelle stellt die Ergebnisse aus der Anlage zusammen.
| n |
Funktion | reelle NS | Periodizität | Grad des Polynoms in x | $\mathtt{\lambda}$-Intervall für Attraktoren |
| 1 | g | 2 Fixpunkte | 1 | 2 | 0 - 1 / 1 - 3 |
| 2 |
g2 | 4 | 2 | 4 | 3 - 1 + $\mathtt{\sqrt{6}}$ |
| 4 |
g4 | 8 | 4 | 16 | 1 + $\mathtt{\sqrt{6}}$ - 3.5440903595... |
| 8 | g8 | 16 | 8 | 256 | noch zu berechnen |
| 3 | g3 | 6 | 3 | 8 | 3.828427124... - 3.841499007... |
| 6 | g6 | 12 | 6 | 64 | noch zu berechnen |
| n | gn | 2n | n | 2n | noch zu beweisen |
Als Beispiele für typisches Aussehen der Funktionen gn(x) - x sollen folgende 2 Grafiken herhalten:
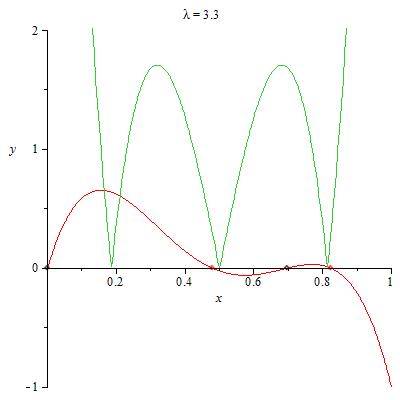
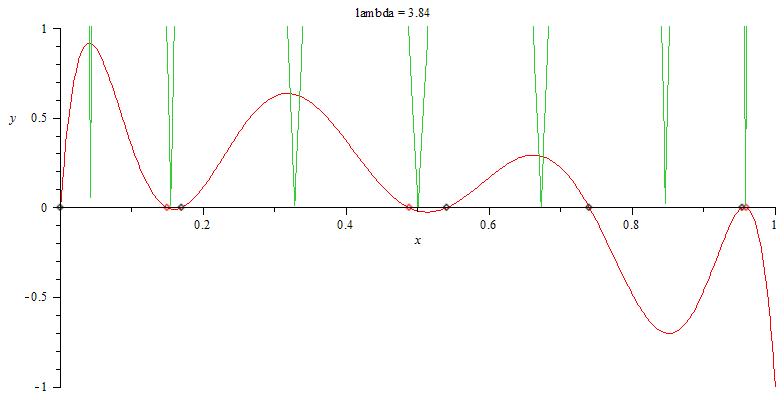
Die erste Grafik stellt g2(x) - x bei $\mathtt{\lambda}$ = 3.3, die zweite g3(x) - x bei $\mathtt{\lambda}$ = 3.84 jeweils in roter Farbe dar. Die grünen Kurven sind die zugehörigen Steigungen der gn nach ihrem Betrag (also |gn'|)
Die roten Nullstellen von gn(x) - x sind attraktive Fixpunkte, die schwarzen Repeller.
Das Feigenbaumdiagramm
Mit Hilfe eines Pascal-Programmes wurden die Folgen (xi) ab $\mathtt{\lambda}$ = 3 für jedes $\mathtt{\lambda}$ bis zu einem hohen Index (5000) berechnet und ab dann wurden die ($\mathtt{\lambda}$, xi)-Punkte zwischen i = 5001 und 7000 eingezeichnet, wobei es letztlich egal ist, bei welchem Wert x0 gestartet wird. Die Attraktoreigenschaft sorgt dann dafür, dass bei diesen hohen Iterationszahlen nur noch der Fixpunkt bzw. eine entsprechende Näherung übrig bleibt. Dabei wurden die bereits im Aufsatz über "Monte Carlo Methoden" benutzten grafischen Units wiederverwendet und wo nötig erweitert.
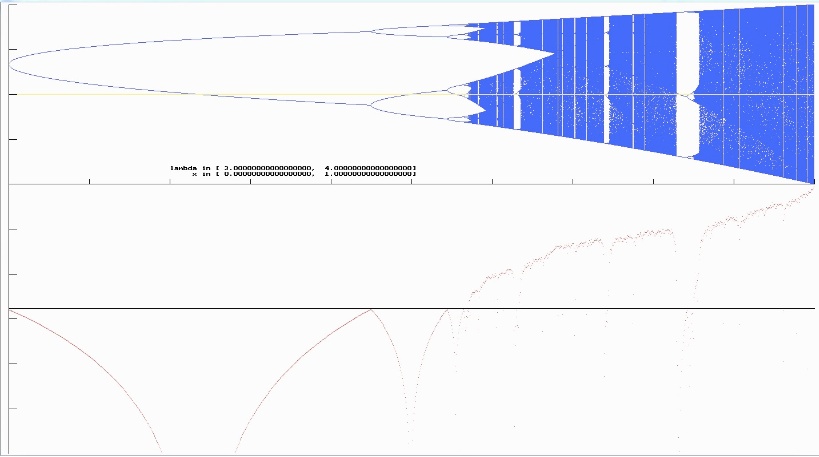
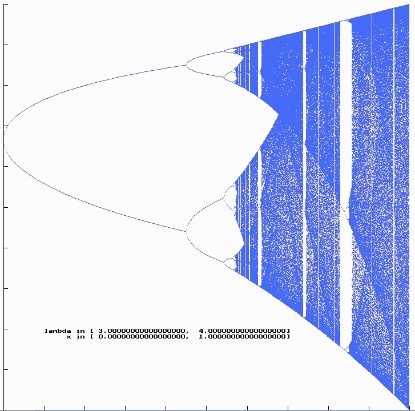
Das erste Diagramm zeigt den vollen $\mathtt{\lambda}$- und x-Bereich [0, 4] x [0, 1].
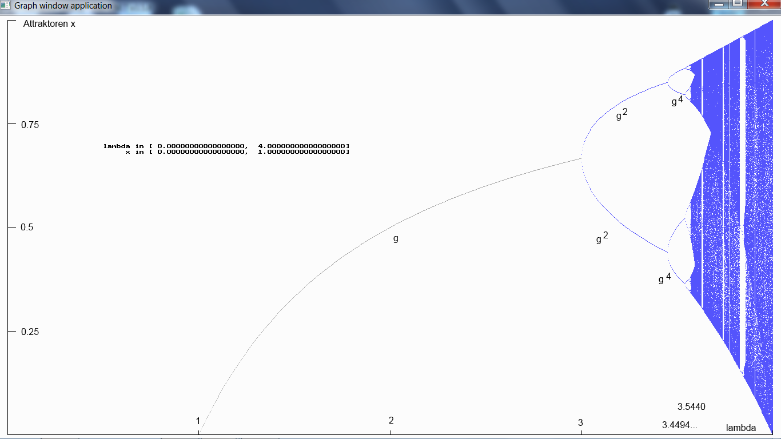
Zwischen 0 und 3 ist der Attraktor der Grenzwert (=Fixpunkt) 0 bzw.
$\mathit{x^\circ = \frac{1 + \lambda + \sqrt{\lambda^2 - 2*\lambda - 3}}{2 * \lambda}}$ (#)
Das Pascalprogramm lässt es zu, auch Ausschnitte des Diagramms darzustellen, der dann die erhöhte Feinheit der $\mathtt{\lambda}$- Schrittweite ausnutzt.
Schauen wir also mal etwas ins Detail:
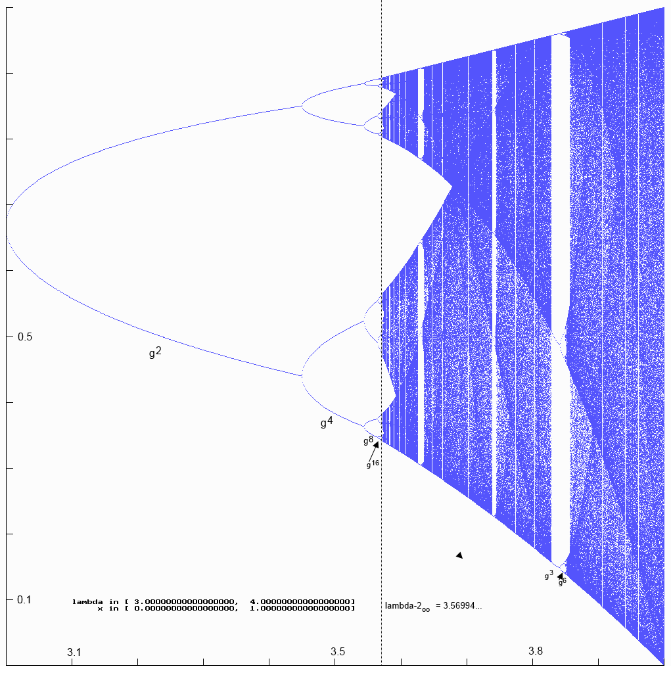
Diese Abbildung ist im Gegensatz zur vorherigen constrained, d.h. die Einheiten auf den Achsen sind gleich groß.
Ich habe neben dem Akkumulationspunkt für 2 auch schon mal zwei Äste der g3 und g6- Bifurkation markiert. Man erkennt gut, dass rechts des Akkumulationspunktes nicht an allen Stellen das Chaos herrscht sondern in vielen "Fenstern" (18) wieder neue Äste von Häufungspunkten mit Bifurkationen aufgrund von Periodenverdopplung auftauchen. Diese Eigenschaft ist eine Komponente der Selbstähnlichkeit (13) oder Skaleninvarianz (14), die typisch für solche fraktalen Mengen (12) ist. Die Äste, die mit g3 beginnen, haben die Besonderheit, dass 3 von den 6 Fixpunkten Attraktoren und 3 Repeller sind, also jeweils eine ungerade Anzahl von Fixpunkten vorhanden sind.
Zunächst aber wieder etwas Mathematik. Die Darstellung der in diesem Diagramm mit gn bezeichneten Äste (von Häufungspunkten xi) kann man als reellwertige Funktionen x($\mathtt{\lambda}$) auffassen (dies geht mit dem Satz über implizite Funktionen, siehe dazu auch Anhang (5)). Ihr links offener Definitionsbereich beginnt mit dem $\mathtt{\lambda}$ des Bifurkationspunktes, (dort ist die Steigung von x($\mathtt{\lambda}$) +∞ oder -∞, die von gn ist dort 1), und endet bei 4 (nach Voraussetzung über den $\mathtt{\lambda}$- Bereich). In den Abbildungen enden die jeweiligen Zweige im nächsten Bifurkationspunkt, da ja nur die Attraktoren eingezeichnet werden sollen. Aber die Fixpunkte von gn bleiben solche mit steigendem $\mathtt{\lambda}$, auch wenn die Steigung betraglich größer 1 wird. Das nächste Diagramm zeigt der Vollständigkeit halber mal die kompletten Äste x($\mathtt{\lambda}$) für die $\mathtt{\lambda}$- Intervalle 1 bis 3 und 3 bis 1 + $\mathtt{\sqrt{6}}$, wobei die Teiläste mit Repellereigenschaft in roter Farbe gezeichnet wurden.
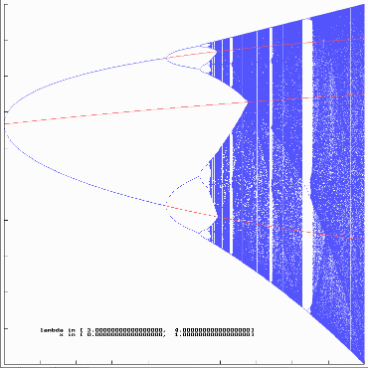
In einer weiteren kleinen grafischen Spielerei habe ich g2 mal als Funktion mit 2 Argumenten $\mathtt{\lambda}$ und x aufgefasst und g($\mathtt{\lambda}$, x) - x 3-dimensional zeichnen lassen. Dies vereinigt - im Ausschnitt für $\mathtt{\lambda}$ aus 3..1 + $\mathtt{\sqrt{6}}$ und x aus 0..1 - die Darstellungen der parameterabhängigen Polynome g2(x) - x (Abbildung 33) als Schnitt senkrecht zur $\mathtt{\lambda}$- Achse und der beiden attraktiven Äste, die am Punkt ($\mathtt{\lambda}$= 3, x = 2/3) bifurkieren, sowie der fortgesetzte rotfarbige Ast mit Repellereigenschaft aus Abbildung 37.
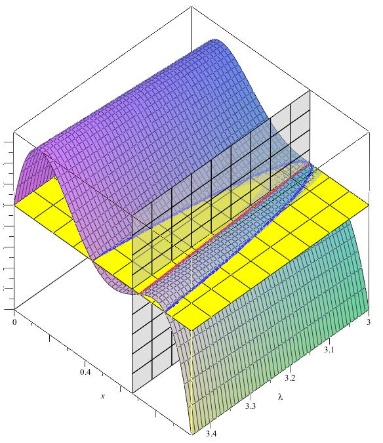
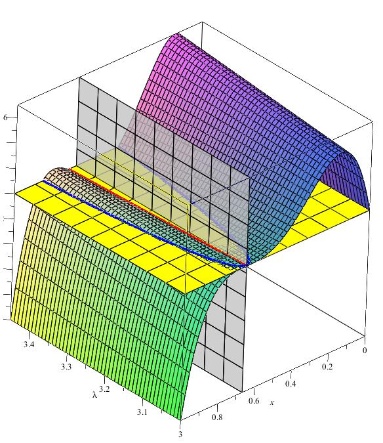
Das zweite Bild zeigt den Bifurkationspunkt bei (3, 2/3). Die gelbe Ebene entspricht der Zeichenebene der Abbildungen 35 - 37 in der in blau die Äste der Verzweigung liegen; die graue transparente Wand zeigt, dass mit wachsendem $\mathtt{\lambda}$ auch der, dann nicht mehr attraktive Bifurkationspunkt, als Nullstelle von g2($\mathtt{\lambda}$, x) - x davon driftet (rote Kurve). Die Parabel der Abbildung 33 findet sich als Schnitt bei $\mathtt{\lambda}$= 3.3.
Als letztes noch zwei Abbildungen der gleichen Art aber zusätzlich mit der 3-dimensionalen Darstellung von g($\mathtt{\lambda}$,x) - x.
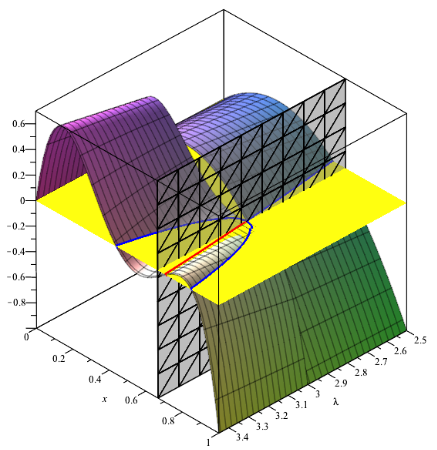
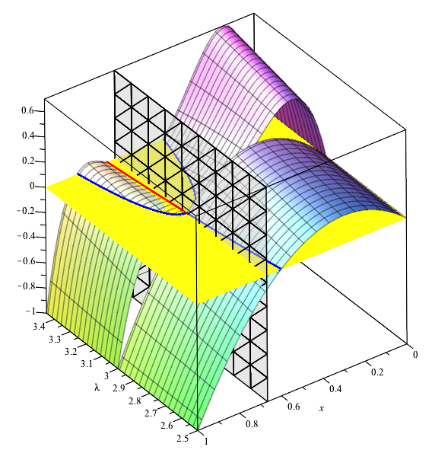
Als dritte Darstellungsmöglichkeit habe ich in dem Buch "Fractals for the Classroom" [10] Histogramme entdeckt, die eine Häufigkeitsverteilung der Iterationspunkte für jeweils festes $\mathtt{\lambda}$ darstellt. Man berechnet die Iterationswerte x0, x1, x2, ..., xm für großes m (Größenordung 106) und ordnet sie in eine äquidistante Intervallaufteilung der Grundmenge [0, 1] ein; die Breite eines solchen Teilintervalles betrage 1/N, es handelt sich also um N Intervalle [(i-1)/N, i/N), i = 1..N. Pro Teilintervall zählt man nun die Anzahl ni der Iterationswerte xk, die in das Intervall fallen. Dann ist $\mathtt{\mu_k := \frac{n_k}{m+1}}$ die relative Häufigkeit (Wahrscheinlichkeit), dass ein Iterationswert in das betreffende Intervall fällt und die trägt man nun grafisch in ein (x, $\mathtt{\mu}$) - Diagramm ein. Die Höhe der entstehenden Rechtecke repräsentieren dann die relative Häufigkeit. Die Verteilung sollte vom Startwert x0 unabhängig sein (bei genügend großem m).
Betrachten wir dazu mal einige Beispiele.
Als erstes vielleicht ein Histogramm aus dem Bereich der Periodizität, sagen wir g8.
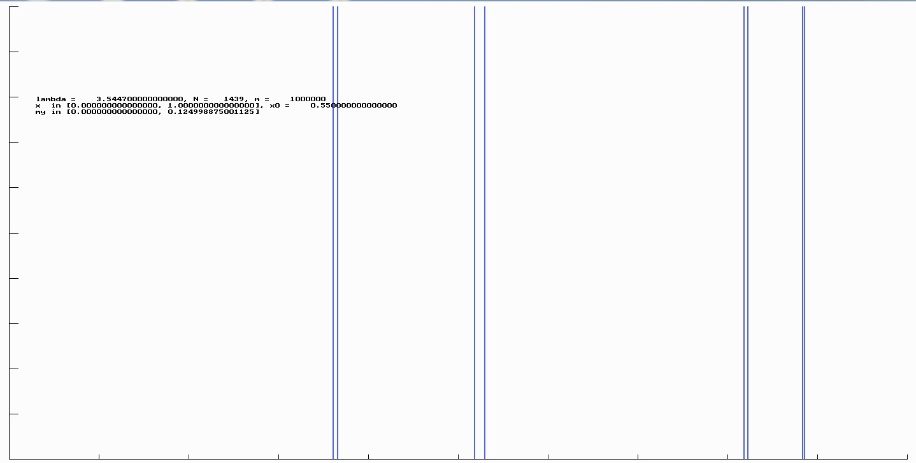
Die eingegebenen Parameter gehen aus der Legende hervor. (Der Wert für N = 1439 ergibt sich aus der auf dem erzeugenden Rechner eingestellte Bildschirmauflösung; die waagrechten Intervalle sind gerade ein Pixel breit.) Dabei ist der rechte Intervallwert des $\mathtt{\mu}$ - Intervalls (hier rund 0.125) die Höhe des höchsten gezeichneten Peeks, also der Peek, der die größte Wahrscheinlichkeit repräsentiert. Natürlich sind bei einem periodischen Orbit (hier 8-Zyklus) alle 8 Peeks gleich hoch (8 * 0.125 = 1). Im Vergleich zum obigen Feigenbaumdiagramm liegen die Peeks selbstverständlich genau an den ausgezeichnete Stellen zum eingegebenen $\mathtt{\lambda}$- Wert.
Mit dem zweiten Diagramm gehen wir ins Chaos und betrachten $\mathtt{\lambda}$= 4, also das Ende des Feigenbaumdiagramms.

Diese "Badewannenkurve" zeigt ein völlig anderes Bild im Vergleich zur geordneten Darstellung im vorherigen Bild, aber hier gehorcht die Oberflächenkurve im Grenzwert einer zu 1/2 symmetrischen Dichteverteilung der Form
$\mathit{v(x) = \frac{1}{\pi\sqrt{x(1-x)}}}$
Wir sehen, dass die Häufigkeit der Iterationen an den Rändern des [0, 1] - Intervalls stark ansteigt.
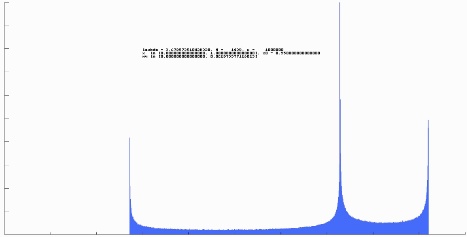
Das dritte Beispiel an dieser Stelle zeigt den Punkt $\mathtt{\lambda}$= 3.6785735104283222652; dies ist die Stelle, an der im Feigenbaumdiagramm die beiden Hauptteile des Diagramms von oben und unten zusammentreffenden. Entsprechend zusammengesetzt ist das Histogramm.
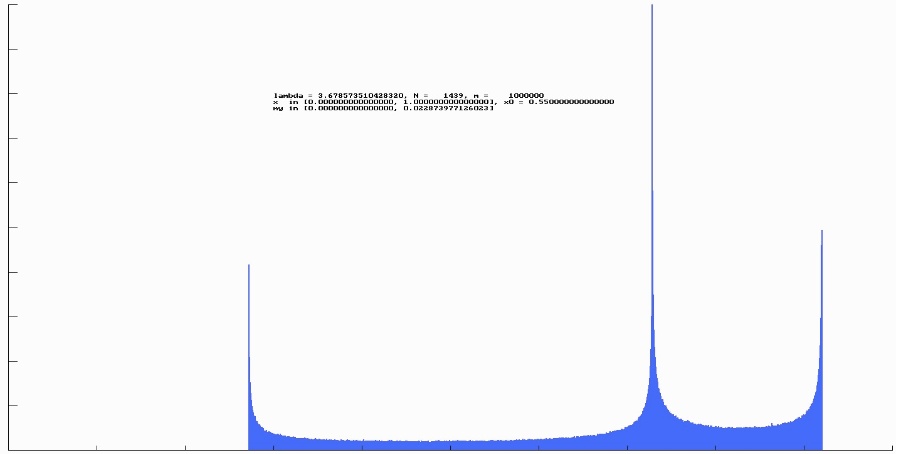
Wir kommen im nächsten Kapitel nochmals auf dieses Histogramm zurück.
Kenngrößen des Feigenbaumdiagramms
Wie im letzten Abschnitt bereits erwähnt, werden in der "Kaskade" von Bifurkationen, die von g2 ausgehen, die $\mathtt{\lambda}$- Intervalle zwischen den Bifurkations - $\mathtt{\lambda}$- Werten so schnell immer kleiner, dass sie einen festen Grenzwert, den ich $\mathit{\lambda\textit{-}2_\infty}$ genannt habe, erreichen aber nicht überschreiten. Dies benutzt man zur Definition der 1. Feigenbaumkonstante $\mathtt{\delta}$:
Defintition 4:
Bezeichne $\mathtt{\lambda_{n-1}}$ den jeweils linken Rand eines Bifurkationsintervalls und $\mathtt{\lambda_{n}}$ den rechten. Dann wird die 1. Feigenbaumkonstante definiert als:
$\mathtt{\delta := \lim_{n \rightarrow \infty}\frac{\lambda_{n}-\lambda_{n-1}}{\lambda_{n+1} - \lambda_{n}}}$
$\mathtt{\delta}$ macht also eine Aussage wie sich die Längen der Bifurkationsintervalle verkürzen, für große n also gerade näherungsweise mit dem Faktor $\mathtt{\frac{1}{\delta}}$.
Betrachten wir unsere obigen Ergebnisse.
$\mathtt{\lambda}$ für g2(x):
$\mathit{\lambda\textit{-}2_0 = 1,\quad \lambda\textit{-}2_1 = 3, \quad \lambda\textit{-}2_2 = 1+\sqrt{6} = 3.4494, \quad \lambda\textit{-}2_3 = 3.5440,}$ so ergibt sich:
$\mathit{\delta_1 = \frac{3-1}{3.4494 - 3} = \frac{2}{0.4494} = 4.45...\quad \textit{(4.7\% Abweichung)}}$
$\mathit{\delta_2 = \frac{3.4494-3}{3.5440 - 3.4494} = \frac{0.4494}{0.0946} = 4.75...\quad \textit{(1.7\% Abweichung)}}$
Nimmt man näherungsweise an, dass die $\mathit{\lambda\textit{-}2_n - \lambda\textit{-}2_{n-1}}$ exakt eine geometrische Reihe bilden, kann man den Akkumulationspunkt $\mathit{\lambda\textit{-}2_\infty}$ angenähert berechnen (siehe Anhang) und erhält 3.56987....
Für die Definition der 2. Feigenbaumkonstante möchte ich etwas weiter ausholen um ein weiteres erstaunliches Ergebnis über die Bifurkationen darzustellen.
Die Funktion g(x), die den Ausgangspunkt unserer logistischen Gleichung darstellt, hat einen kritischen Punkt, also einen Punkt bei dem die erste Ableitung den Wert Null annimmt; dies ist für $\mathtt{g'(x) = \lambda (1-2x)}$ der Wert x=1/2 (natürlich für $\mathtt{\lambda}$ <> 0). Dieser Wert ist von $\mathtt{\lambda}$ unabhängig. Setzt man ihn in g ein, $\mathtt{g(\frac{1}{2})= \frac{\lambda}{2}(1-\frac{1}{2}) = \frac{\lambda}{4}}$, so liegt für $\mathtt{\lambda}$ = 2 ein superstabiler Fixpunkt von g vor. So weit so gut.
Zieht man nun im Feigenbaumdiagramm in der Höhe x=1/2 eine Parallele zur $\mathtt{\lambda}$- Achse, so schneidet diese Gerade für jedes Bifurkationsintervall in der Folge der bei g2 startenden Kaskade genau einen Ast.
Dies sehen wir uns an.
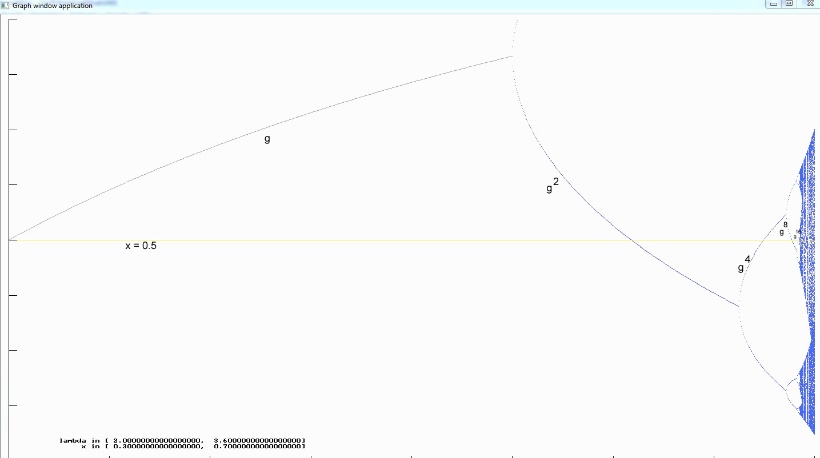
Die gelbe Linie ist die Parallele in Höhe 1/2, die erkennbar Äste von g, g2, g4, g8 und gerade noch erkennbar g16 schneidet.

Dieser Ausschnitt vom rechten Bildrand zeigt Schnittpunkte zu g4, g8, g16, g32 und g64, wenn man das Bild durch Mausklick vergrößert. Aber man erkennt auch noch, dass Äste anderen Ursprungs in dem großen Fenster weiter rechts ebenfalls geschnitten werden. Diese Tatsache muss natürlich bewiesen werden und ist ein tiefliegendes Ergebnis der Untersuchungen von Feigenbaum (siehe dazu auch den Anhang dieses Kapitels).
Wir wollen nun die $\mathtt{\lambda}$- Werte der Schnittpunkte der 0.5 - Parallele mit den Ästen $\mathtt{g^{2^{n}}}$ mit $\mathtt{\Lambda_n}$ benennen ($\mathtt{\Lambda}$ groß geschrieben), also $\mathtt{g^{2^{n}}(\Lambda_n,\frac{1}{2}) = \frac{1}{2}}$.
Wie aus Zusatz 3.2 in den "Theoretischen Ergebnisse zur n-Periodizität ..." (3) hervorgeht, taucht in der ersten Ableitung von $\mathtt{g^{2^{n}}}$ als Faktor die erste Ableitung von g auf. Die hat aber, wie oben schon bemerkt, für alle $\mathtt{\lambda}$ an der Stelle x=1/2 den Wert 0! Somit gilt:
($\mathtt{g^{2^{n}}}$)' (1/2) = 0, was einerseits bedeutet, dass 1/2 kritischer Punkt für alle $\mathtt{g^{2^{n}}}$ ist, andererseits liegen bei den $\mathtt{\Lambda_n}$ Superzyklen (und übrigens nur da) vor.
Nun bezeichnet man die (vorzeichenbehafteten) Abstände parallel zur x-Achse zwischen zwei zueinandergehörigen Ästen mit dn, wobei n bei 1 beginnend durchnummeriert wird (siehe folgende Skizze). Formal schreibt sich
$\mathtt{d_n = g^{2^{n}}(\Lambda_n, \frac{1}{2}) - \frac{1}{2}}$
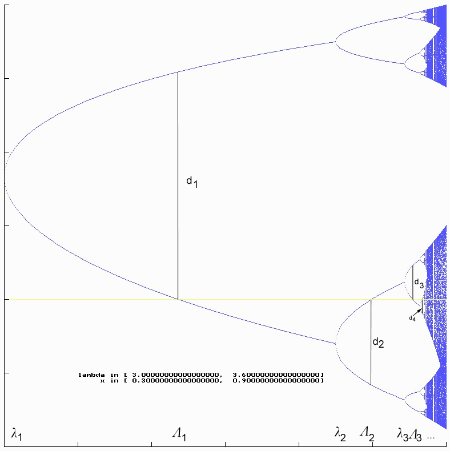
Die Darstellung ist constrained.
Definition 5:
Die 2. Feigenbaumkonstante $\mathtt{\alpha}$ wird definiert durch:
$\mathtt{\alpha := - \lim_{n \rightarrow \infty} \frac{d_n}{d_{n+1}}}$
Da immer entweder dn oder dn+1 negativ sind, ist $\mathtt{\alpha}$ positiv. Ihr numerisch bestimmter Wert liegt bei $\mathtt{\alpha}$ = 2.5029078750...
Die Bedeutung dieser Konstanten liegt unter anderem in der Methode, die wesentlichen Aussagen dieser Kapitel, speziell auch die Periodenverdopplung zu beweisen. Sie ist Bestandteil des sog. Verdopplungsoperators (siehe Anhang).
Berechnen wir nun für unser g die ersten Schnittpunkte von x=0.5 mit den Ästen, die aus den $\mathtt{g^{2^{n}}}$ entstehen (für m = 1, 2 und 4), d.h. löst man die Gleichungen $\mathtt{g^{2^{n}}(\Lambda_n,\frac{1}{2}) = \frac{1}{2}}$ (wobei g hier wieder als Funktion beider Argumente $\mathtt{\lambda}$ und x geschrieben wird), so ergeben sich folgende Werte:
| 2n |
$\mathtt{\lambda}$ |
x-Werte |
| 1 |
2 |
0.5 |
| 2 |
$\mathtt{2},\quad \mathbf{\Lambda_1 = 1 + ˜\sqrt{5} = 3.236067977...,}\quad \mathtt{1 - \sqrt{5}}$ |
0.5, 0.809016994 |
| 4 | $\mathtt{2, \quad 1+\sqrt{5},\quad 1-\sqrt{5}, \quad} \mathbf{\Lambda_2=3.4985616993..., \quad ... }$ |
0.5, 0.383598230 |
Die fett gedruckten Zahlen sind für unsere Berechnung relevant, dazu gehören die x-Werte in der dritte Spalte.
d1 = 0.809016994 - 0.5 = 0.309016994
d2 = 0.383598230 - 0.5 = - 0.11640177
und eine erste Näherung für $\mathtt{\alpha}$ als $\mathtt{-\frac{d_1}{d_2} = 2.538...}$
In der Folge der $\mathtt{g^{2^{n}}}$ wechseln sich die Bifurkationspunkte ($\mathtt{\lambda_{n}}$) mit denen der Superstabilität ($\mathtt{\Lambda_n}$) ab (siehe Abbildung 44). Sowohl $\mathtt{\lambda_{n}}$ als auch $\mathtt{\Lambda_n}$ konvergieren gegen den(-selben) Grenzwert, den wir bisher $\mathit{\lambda\textit{-}2_\infty}$ genannt haben.
Der folgende Anhang ist sehr umfangreich. Er beschreibt Wege zum Beweis der Feigenbaumschen Vermutungen und beinhaltet neben vielen Abbildungen auch numerische Ergebnisse zur Berechnung der Feigenbaumkonstanten und des Feigenbaumpunktes.
Theoretische Überlegungen zu den Feigenbaumkonstanten
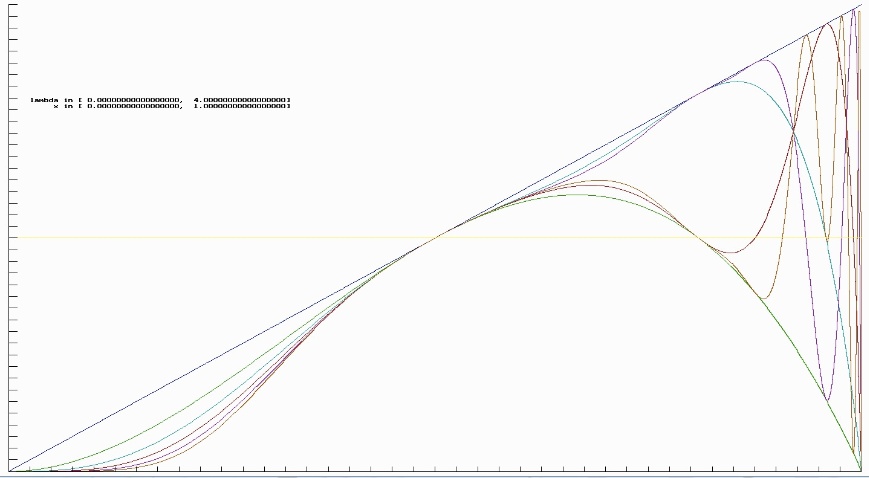
Ein weiteres Phänomen schließt sich hier an. Dazu betrachten wir wiederum g als g($\mathtt{\lambda}$, x) und untersuchen das Aussehen der Funktionen $\mathtt{g^n(\lambda, \frac{1}{2})}$, d.h. hierbei werden die gn bzgl. $\mathtt{\lambda}$ nicht auf das Bifurkationsintervall beschränkt in dem die Orbits aus Attraktoren bestehen, sondern $\mathtt{\lambda}$ variiert zwischen 0 und 4.
Ich habe mit Maple die ersten 4 der $\mathtt{g^n(\lambda, \frac{1}{2})}$ berechnet und zusammen mit der Konstanten in Höhe 1/2 in ein ($\mathtt{\lambda}$- x)-Diagramm gezeichnet.
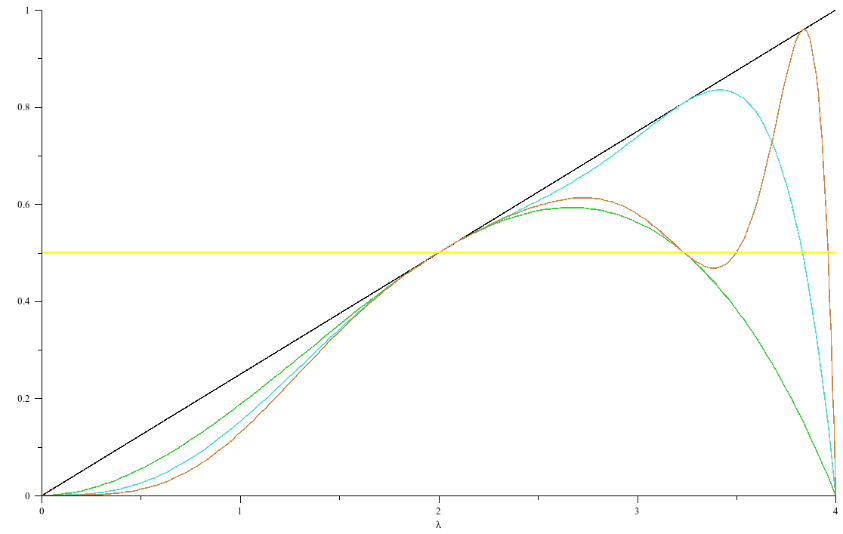
Dabei sind die gn (hier n=1..4) nach schwarz, grün, türkis und braun sortiert. Dieses Diagramm wurde gezeichnet indem die gn explizit bestimmt und dann als Funktionen gezeichnet wurden.
Eine andere Methode zu einem solchen Bild zu kommen besteht darin, bei der Zeichnung des Feigenbaumdiagramms, das ja keine explizite Kenntnis der gn benötigt (außer g natürlich), für jedes $\mathtt{\lambda}$, beginnend beim Startwert x0 = 1/2 (!) die ersten n Iterationen als ($\mathtt{\lambda}$, xi) - Punkt (i=1..n) einzuzeichnen.
Das folgende Bild stellt diese Kurven ebenfalls für n=4 zunächst ohne die Punkte des Feigenbaumdiagramms dar (sie wurden programmtechnisch ausgeblendet).
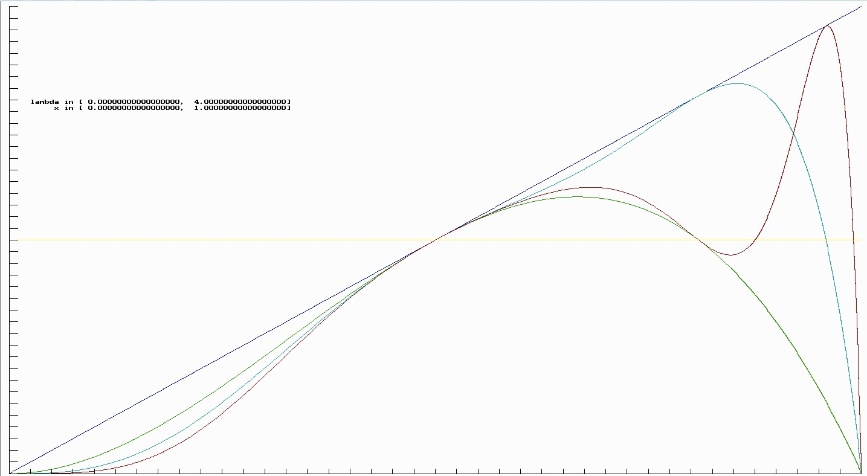
Es wurden die gleichen Farben wie oben verwendet.
Diese Kurven werden aus nahe liegenden Gründen auch als "critical value lines" bezeichnet (siehe z.B. [10]).
Das Einschalten der Diagrammpunkte zeigt nun die volle Schönheit des zusammengesetzten Diagramms und welche begrenzende Bedeutung diese Kurven haben. (Weiterhin findet man im Anhang den Zusammenhang dieser Kurven zu Kneadingfolgen, siehe dort.)
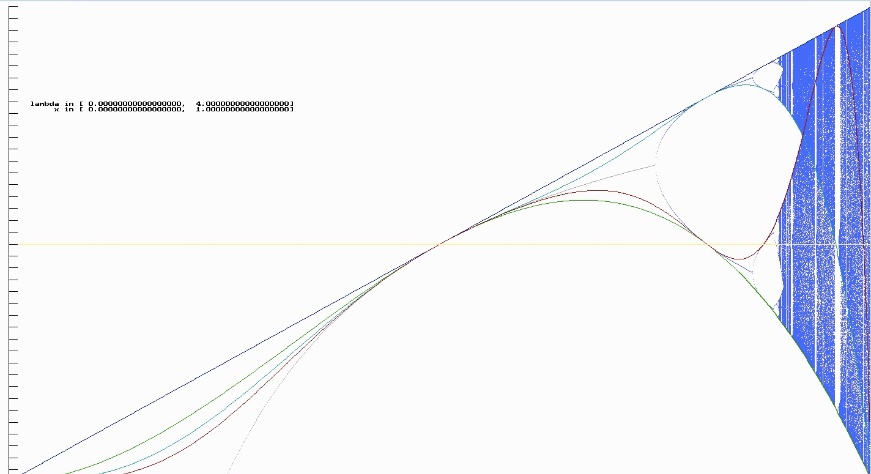
Um den Effekt noch etwas deutlicher darzustellen, habe ich den Ausschnitt ab $\mathtt{\lambda}$ = 3 einmal mit und einmal ohne die critical value lines gezeichnet.
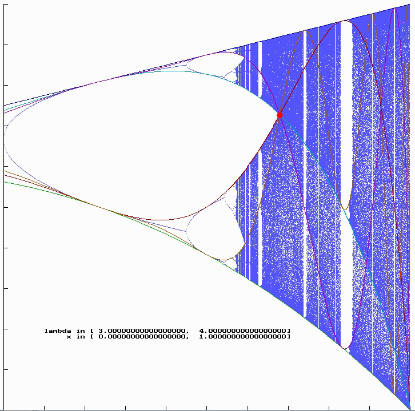
Man erkennt, dass im Bild 47a die critical value lines als Konturen sichtbar zu sein scheinen. Dies sind aber keine realen, im Feigenbaumdiagramm vorhandenen Kurven, sondern die Konturen entstehen durch unterschiedliche Dichten der Orbitpunkte entlang eben dieser Konturen. Erinnern wir uns an das Histogramm für $\mathtt{\lambda}$ = 3.6785735104283222652 aus dem letzten Kapitel (Abbildung 41c). Der mittlere Peek bei x = 0.728155493653961819 zeigt die Häufigkeitsverteilung um den korrespondierenden Punkt (3.6785735104283222652, 0.728155493653961819), den ich im obigen Diagramm (47b) rot markiert habe und der Schnittpunkt der critical value lines ist. Die Verteilung zeigt gerade, dass an dieser Stelle eine Häufung der Orbitwerte vorliegt, die im Diagramm 47a als scheinbarer Schnittpunkt zu sehen ist.
Wandert man nun mit $\mathtt{\lambda}$ nach links oder rechts etwas aus diesem Punkt heraus, so müssten sich im Histogramm an den Stellen der Konturen zusätzliche Peeks zeigen und der Schnittpunktpeek verschwinden. Tatsächlich sieht man auf dem nächsten Diagrammen diese Peeks, die gemäß numerischer Berechnung genau an den richtigen Stellen sitzen.
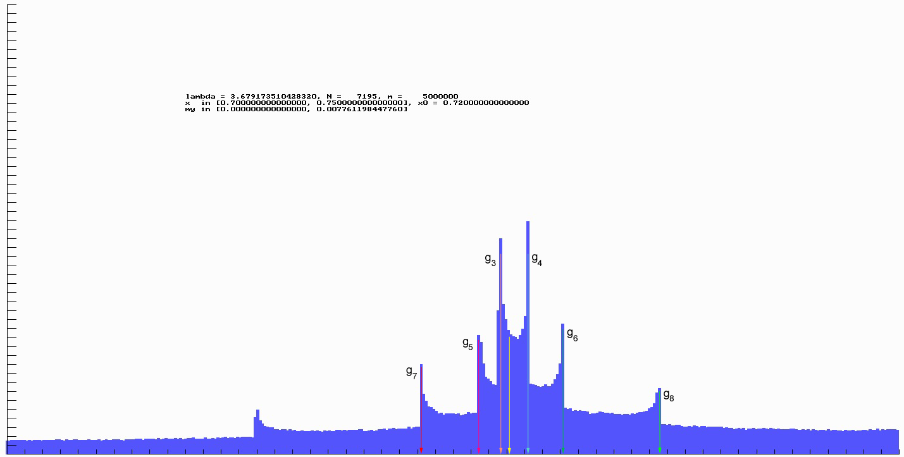
In diesem Bild wurde $\mathtt{\lambda}$ um 0.0006 erhöht, der Ausschnitt zeigt das Intervall [0.7, 0.75]. Die erwarteten Werte für die gn sind in der folgenden Tabelle zusammengestellt und gut erreicht.
| n |
gn = gn(3.6785735104283222652 + 0.0006, 0.5) | Farbe |
| 3 |
0.72757 |
orange |
| 4 |
0.72925 |
türkis |
| 5 | 0.72642 | violett |
| 6 | 0.73117 | dunkelgrün |
| 7 | 0.72317 | rot |
| 8 | 0.73654 | hellgrün |
| Schnittpunkt | 0.72816 | gelb |
Natürlich ist durch n = 4 für die critical value lines keine Obergrenze erreicht. Da die gn nicht explizit als Funktion berechnet werden müssen, kann man theoretisch mit geringem Rechenaufwand beliebig hohe n benutzen, aber der zeichnerischen Darstellung sind dann bald Grenzen gesetzt. Schon bei n = 6 wird's am rechten Rand unübersichtlich.
Wieso liefern die beiden Zeichenmethoden das gleiche Ergebnis? Nun, durch das jeweilige Starten der Iteration bei 1/2, werden nacheinander für jedes $\mathtt{\lambda}$ die Funktionswerte $\mathtt{g(\lambda, \frac{1}{2})}$, $\mathtt{g(g(\lambda, \frac{1}{2})) =g^2(\lambda, \frac{1}{2}), ...}$ berechnet, was der Zeichnung der $\mathtt{g^n(\lambda, \frac{1}{2})}$ gleichkommt.
Der Lyapunov-Exponent.
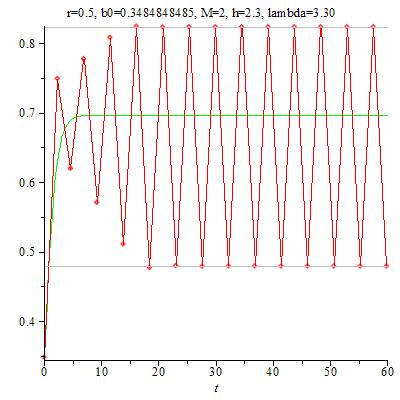
Im Anhang "Gütekriterien numerischer Verfahren" habe ich im Abschnitt "Kondition" ausgeführt, dass ein numerisches Verfahren bei geringer Änderung der Eingabewerte auch nur geringfügig geänderte Ergebniswerte liefern sollte, sonst ist es letztlich unbrauchbar. In unserem Zusammenhang ist der wesentliche Eingabewert der Startwert x0 der Iteration und, wir erinnern uns, dass die xi eine durch Diskretisierung entstandene Zeitreihe (mit viel zu großem h) darstellen. Jedenfalls liegt eine solche "Sensitive Abhängigkeit von den Anfangswerten" (7) vor - einen Begriff, den man natürlich auch exakt definieren muss (siehe [1], Kap.5) -, was sich schon nach relativ wenigen Interationsschritten zeigen kann. Betrachten wir dazu ein Beispiel:
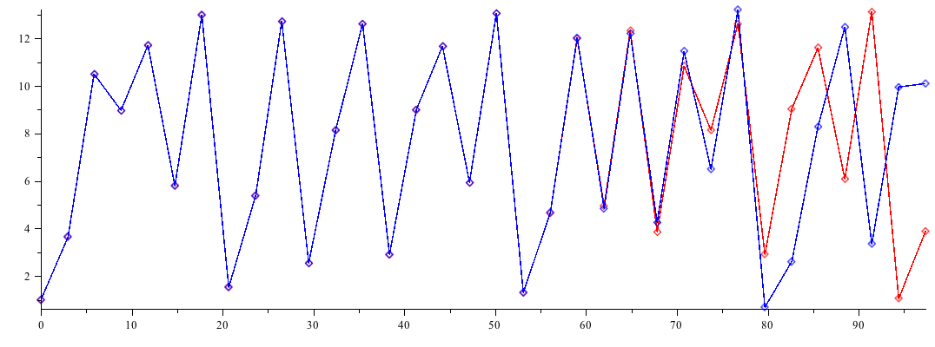
Hier wurde mit r = 0.1, M = 10 und h = 2.95 gerechnet, was einem $\mathtt{\lambda}$- Wert von 3.95 entspricht; die rote Kurve hatte einen Iterationsstartwert von 1, die blaue einen von 1.0000001. Ab der 20. Iteration wird graphisch eine Abweichung sichtbar, die kurz darauf zu völligem Auseinanderlaufen der Iterationen führt. Freilich, nur bei genügend kleinem h ist die Kondition des zugrunde liegende Eulerverfahrens gut. Betrachtet man die errechneten Zahlenwerte, sieht man, wie die roten und die blauen Werte langsam aber sicher auseinander laufen was auch bei der schlechten Kondition des Verfahrens bei diesen Parametern nicht verwundern kann.
Auszug aus den Iterationswerten:
| Iteration |
Zeit | rote Kurve |
blaue Kurve |
Abweichung % |
| 0 |
0 | 1 |
1.0000001 |
0.00001 |
| 1 |
2.95 | 3.655 |
3.655000336 |
0.000009 |
| 2 | 5.90 | 10.49633762 | 10.49633823 | 0.000006 |
| 5 | 14.75 | 5.803959305 | 5.803953920 | 0.00009 |
| 10 | 29.50 | 2.54342684 | 2.54333870 | 0.003 |
| 15 | 44.25 | 11.66592753 | 11.66786896 | 0.02 |
| 20 | 59.00 | 11.98866537 | 12.02534326 | 0.3 |
| 30 | 88.50 | 6.087099534 | 12.47612432 | 104 |
Eine grundsätzliche Aussage über die sensitive Abhängigkeit von den Anfangswerten findet sich z.B. in [1], Satz 5.17. Danach garantiert die Existenz eines stabilen Orbits (n-Zyklus), dass keine sensitive Abhängigkeit von den Anfangswerten vorliegt (die genaue Formulierung ist etwas formaler, aber zum Verständnis reicht es).
Aber ich hatte ja versprochen, etwas über die Meßbarkeit des Chaos zu berichten.
Zu diesem Zweck wird der Lyapunov-Exponent L(x0) (8) verwendet, dessen Definition von folgender Idee ausgeht:
Wackelt man an einem Startwert x0 etwas, also $\mathtt{x_0 + \epsilon}$ (mit $\mathtt{\epsilon}$> 0), und iteriert beide Werte n mal, kann man die Differenzen von Startwert und gestörtem Startwert einerseits, also $\mathtt{\epsilon}$, und deren Iterierten $\mathtt{f^n(x_0 + \epsilon) - f^n(x_0)}$ andererseits vergleichen. Der Lyapunov-Exponent ist nun nicht etwa einfach der Quotient der Differenzen, sondern man geht von einem n-abhängigen exponentiellen Ansteigen oder Abfallen der zweiten Differenz im Vergleich zur ersten aus:
$\mathtt{\epsilon \exp({n L_n(x_0)}) = |f^n(x_0 + \epsilon) - f^n(x_0)| \Leftrightarrow L_n(x_0) = \frac{1}{n}ln{\frac{|f^n(x_0+\epsilon)-f^n(x_0)|}{\epsilon}}}$
$\mathtt{L(x_0)=\lim_{n \rightarrow \infty} \frac{1}{n} \sum^{n-1}_{i=0} \ln{(|f'(x_i)|)} \texttt{ mit } x_i = f^i(x_0) \texttt{, also die Iterierten.}}$
- existiert der Grenzwert überhaupt
- kann er uneigentlich werden
- ist der Grenzwert tatsächlich von x0 abhängig oder nicht
Jedenfalls spricht man, motiviert durch obige Einführung, von einer sensitiven Abhängigkeit von den Anfangswerten, wenn L(x0) > 0 ist, bei L(x0) < 0 wirkt sich eine Störung der Anfangswerte nicht durch Auseinanderdriften der Orbits aus.
Die Anwendung auf g(x) lässt sich wiederum schön als Diagramm darstellen, hier bekommt das Feigenbaumdiagramm einen Anhang, der Spreu vom Weizen trennt, d.h. für jedes $\mathtt{\lambda}$ kann man eine Aussage über Chaos oder nicht erhalten.
Das Pascal Programm für den Feigenbaum habe ich erweitert und zeige als erstes den interessanten Bereich von $\mathtt{\lambda}$ = 1..4. Die Werte des Lyapunow-Exponenten sind unterhalb als rote Punkte eingezeichnet, wobei die Parallele zur $\mathtt{\lambda}$- Achse unterhalb den Nullwert für L kennzeichnet.

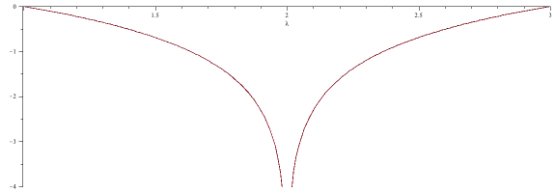
Die gelbe Parallele zur $\mathtt{\lambda}$- Achse in Höhe von x=0.5, die wir schon im Kapitel über die Kenngrößen benutzt haben, zeigt in den Schnittpunkten zu den Bifurkations-Ästen des Diagramms gerade die Stellen des negativen uneigentlichen Grenzwertes des Lyapunow-Exponenten. Für die beiden $\mathtt{\lambda}$- Bereiche [1, 3] und $\mathit{[3, 1 + \sqrt{6}]}$ kann man den Exponenten geschlossen berechnen. Für [1, 3] erhält man $\mathit{L = \ln{(|2-\lambda|)}}$, für $\mathit{[3, 1 + \sqrt{6}]}$ kommt $\mathit{L=\frac{1}{2} \ln{(|\lambda^2 - 2 \lambda - 4|)}}$ heraus. (Beide Ergebnisse sind im Anhang zu diesem Kapitel hergeleitet.) Zeichnet man die beiden Funktionen in Abhängigkeit von $\mathtt{\lambda}$, sieht man gerade die in Abbildung 51 bzw. 53 gezeichneten Kurven:
Hier liegt der negative uneigentliche Grenzwert (-∞) bei $\mathtt{\lambda}$ = 2.
Und für den Bereich $\mathit{[3, 1 + \sqrt{6}]}$:

Hier wird -∞ bei $\mathit{\lambda = 1 + \sqrt{5} = 3.23606...}$ erreicht (siehe dazu auch die Zeile 2 in der Tabelle des letzten Kapitels).
Ab $\mathit{\lambda = 1 + \sqrt{5} = 3.23606...}$ beginnt der Bereich in dem Chaos herrscht (L ist > 0), bis auf die vielen Fenster, in denen das Chaos aussetzt (L < 0). Betrachten wir das größte Fenster mal genauer; man erkennt in der Spreizung schön, wie L in den negativen Bereich absinkt und ab einem Akkumulationspunkt $\mathit{\lambda\textit{-}3_\infty}$ wieder positiv wird.

Im Übrigen kann man berechnen, dass L für $\mathtt{\lambda}$ = 4 den Wert ln(2) = 0.69314 ... annimmt, das Maximum der Werte für L im Bereich [1, 4].
An den Stellen, an denen L den Wert -∞ annimmt, liegt, wie schon im letzten Kapitel erwähnt, ein Superzyklus vor.
Eine weitere Interpretation des Lyapunow-Exponenten, die ich im Buch von H. G. Schuster und W. Just [2] gefunden habe, ist informationstechnischer Art. Man kann den Lyapunow-Exponenten nämlich auch als Maß für den Informationsgewinn oder -verlust über die Lage der Iterationswerte durch die Iterationen auffassen. Die Autoren leiten aus der von der Shannonschen Informationstheorie bekannten Formel
$\mathtt{I = - \sum^n_{i=1}p_i ld(p_i)}$
$\mathtt{\Delta I = -\lim_{n \rightarrow \infty}\frac{1}{N}\sum^{N-1}_{i=1} ld(|f'(x_i)|)}$
Bleibt zu bemerken, dass für $\mathtt{\lambda}$ = 4 der Informationsverlust (gemäß oben angegebenem Wert) ∆I = 1, also total ist.
Theoretische Aussagen zum Lyapunow-Exponent
Fenster auf, Fenster zu: ich krieg die Krise
- Bisher haben wir uns fast ausschließlich mit der zum Chaos führenden Periodenverdopplung beschäftigt. Ist dies die einzige Möglichkeit chaotisch zu werden?
- Der Begriff des Fensters, also $\mathtt{\lambda}$- Bereiche, in denen das Chaos aussetzt und wieder Bifurkationsäste auftauchen, wurde schon an mehreren Stellen dieses Artikels verwendet. Aber wie kommt es überhaupt dazu, dass plötzlich wieder Ordnung in das Konvergenzverhalten einzieht und welche Fenster gibt es?
Bei der Formulierung benutze ich als Grundlage das Buch von Metzler [1], passe aber die Bezeichnungen unserer Nomenklatur an.
Ich habe diesen Satz nicht in einen Anhang verbannt, da seine Hauptvoraussetzung ohnehin hier dargestellt werden muss und der Rest eine Kleinigkeit ist. Diese Hauptvoraussetzung ist nach meiner Erfahrung sehr ungewöhnlich - sofern man eine solche Bewertung in der Mathematik überhaupt treffen kann. Es handelt sich um eine bestimmte Anordnung der natürlichen Zahlen, die man am besten versteht, wenn man die folgenden Anweisungen durchführt:
- Ordne die ungeraden Zahlen (außer 1) beginnend bei 3 aufsteigend an
- Multipliziere unter Beibehaltung der Reihenfolge alle Zahlen aus 1. mit 2
- Multipliziere unter Beibehaltung der Reihenfolge alle Zahlen aus 1. mit 22
- Multipliziere unter Beibehaltung der Reihenfolge alle Zahlen aus 1. mit 23
...
n. Multipliziere unter Beibehaltung der Reihenfolge alle Zahlen aus 1. mit 2n
...
∞. Ordne die Potenzen von 2 absteigend bis 20 = 1
So sieht also dann das Ergebnis aus (ich benutze als Symbol für die Sarkovskii Sortierung das normale > Zeichen, die Tastatur gibt nichts Besseres her):3 > 5 > 7 > ....
2*3 > 2*5 > 2*7 > ....
22*3 > 22*5 > 22*7 > ....
....
2n*3 > 2n*5 > 2n*7 > ....
....
.... > 24 > 23 > 22 > 2 > 1
Somit ist die 3 (!) die "größte" oder auch die letzte Zahl dieser Sortierung.
Zumindest die letzte Zeile lässt schon ahnen, was da kommt:
Satz von SarkovskiiSei $\mathtt{f:[a, b] \rightarrow \mathbb{R}}$ (oder auch $\mathtt{f:\mathbb{R} \rightarrow \mathbb{R}}$) stetig und besitze einen periodischen Orbit der Ordnung k (k-Zyklus). Dann hat f auch periodische Orbits der Ordnung l (l-Zyklen) für alle l < k im Sinne der oben eingeführten Sarkovskii Sortierung.
Und das war's schon! Man kann es kaum glauben.
Angewendet auf die logistische Gleichung mit $\mathit{g(\lambda, x) := \lambda x (1-x)}$ muss man nun noch etwas Zusätzliches bedenken. Die Abhängigkeit der Funktion g von $\mathtt{\lambda}$, die ich mal wieder extra aufgeschrieben habe, verbietet die direkte Anwendung des Satzes auf $\mathit{g(\lambda, x)}$; vielmehr hat man für jedes $\mathtt{\lambda}$ ein eigenes f. Was tun? Wenden wir mal Sarkovskii auf die Funktion $\mathit{g(1+\sqrt{8}, x)}$ an. Ab da haben wir im Anhang (4) einen 3-Zyklus von $\mathit{g(\lambda, x)\quad (1+\sqrt{8} < \lambda < 3.8415...)}$ gefunden. Nach Sarkovskii muss es dann auch für jedes andere n einen Zyklus geben, da 3 ja "größte" Zahl in der Sortierung ist. Wo sind diese Zyklen? Betrachten wir dazu nochmals die Abbildungen 36 und 37 aus dem Kapitel über das Feigenbaumdiagramm. In 36 habe ich das Fenster für die 3er Periode kenntlich gemacht. In 37 sind die Repeller von g und g2in rot eingezeichnet. Beides habe ich in den nächsten beiden Abbildungen zusammengefasst und unter die Lupe gelegt. Man kann Fenster für die Perioden 3, 5, 7 und gerade noch 9 sowie 6 und 10 erkennen.
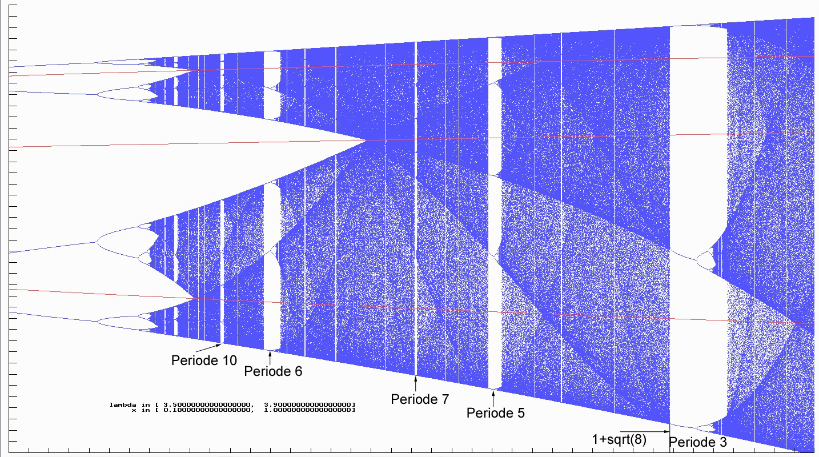
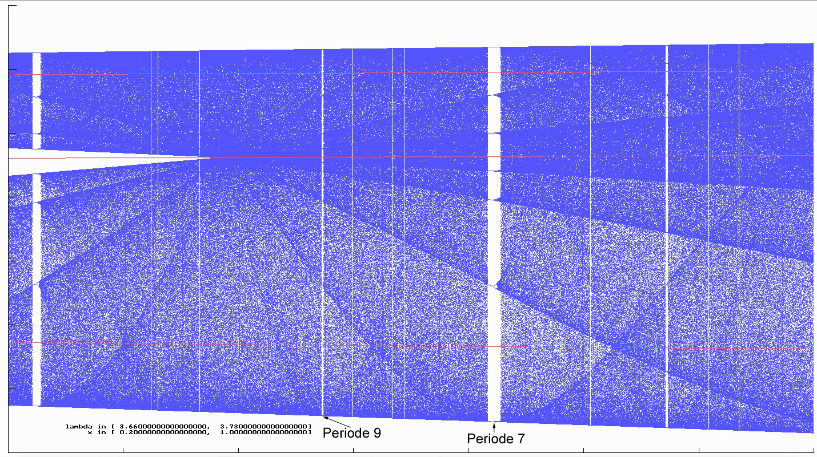
Die roten Repeller müssten eigentlich für jeden Bifurkationspunkt, an dem sie ja zu Repellern werden, bis zum rechten Ende des Diagrammes durchgezeichnet werden - beispielhaft habe ich ja nur die ersten 3 eingezeichnet. Dann wäre auch schon im Fenster zur Periode 3 alles rot und wir würden sehen, wo die anderen Orbits, die Sarkovskii behauptet, liegen. Auch wieder als Beispiel seien die beiden zu g2 gehörigen Repeller dort betrachtet. Für $\mathtt{\lambda}$ = 3.83 befinden wir uns im 3er Fenster und können die beiden Orbitpunkte aus den mit (#) und (##) bezeichnete Formeln im Kapitel "Das deterministische Chaos" berechnen:
x3 = 0.8919352170 und x4 = 0.3691613885 sind die Werte und natürlich bilden sie einen 2-Zyklus, was man durch Einsetzen in g2(3.83, x) leicht verifiziert.
Entsprechend finden sich alle anderen links des 3er Fensters "unsichtbar" gewordenen Zyklen dort wieder, wie der Satz von Sarkovskii ja gerade verspricht. Dass es tatsächlich immer nur einen stabilen Orbit (Attraktor) gibt und alle anderen instabil (Repeller) sind, ist kein Zufall, sondern wird durch einen entsprechenden Satz festgeschrieben (siehe Anhang (5), Satz 1). Danach attrahiert eine S-unimodale Abbildung höchstens einen kritischen Punkt.
Da unsere logistische Abbildung nur den einen kritischen Punkt bei x=1/2 hat und S-unimodal ist, gibt es also jeweils höchstens einen Attraktor.
Um einem Missverständnis direkt vorzubeugen; der Satz von Sarkovskii sagt nichts über die Anzahl der jeweiligen Zyklen aus, insbesondere gibt es auch keine Eindeutigkeitsaussage, sondern nur eine Existenzaussage. Z.B. gibt es drei 5-Zyklen bei der log. Gleichung, dazu unten mehr.
Bleiben wir noch etwas beim 3er Zyklus, er hat so ein schönes breites Fenster und man kann eine Menge neuer Phänomene an ihm feststellen. Überhaupt stellt sich als erstes die Frage, wie er entsteht. Eine Bifurkation, wie wir sie bei den 2k-Zyklen kennengelernt haben, tritt erst wieder auf, nachdem er schon existiert, also rechts von dem Wert $\mathtt{1+\sqrt{8}}$. Aber wie wühlen sich die 3 Äste aus dem links von $\mathtt{1+\sqrt{8}}$ herrschenden Chaos heraus? Einen ersten Eindruck davon gibt die letzte Abbildung im Anhang (4), wo ja der 3-Zyklus gerade bei seiner Geburt dargestellt wurde ($\mathtt{\lambda}$ = $\mathtt{1+\sqrt{8}}$, auf 20 Stellen genau). An 3 Stellen berührt die gezeichnete rote Funktion $\mathit{g^3(1+\sqrt{8}, x)-x}$ die x-Achse, hier liegt jeweils eine 2-fache Nullstelle dieser Funktion vor. Mit wachsendem $\mathtt{\lambda}$ zerfließen die 2-fachen Nullstellen in jeweils zwei (also insgesamt 6) einfache Nullstellen, von denen 3 den stabilen und die anderen 3 den instabilen Zyklus darstellen (wie man ebenfalls in diesem Anhang in der Abbildung für $\mathtt{\lambda}$ = 3.84 sehen kann). Für die Aussage über die Ordnung der Nullstellen siehe Anhang (3) Zusatz 3.1.
Vielfach wird in der Literatur der Graf von g3(x) und x in ein Diagramm gezeichnet und der Begriff Tangentenbifurkation (17) damit begründet. Die nächste Abbildung zeigt dies für drei $\mathtt{\lambda}$ von denen das mittlere (=rote Kurve) gerade $\mathtt{1+\sqrt{8}}$ ist.
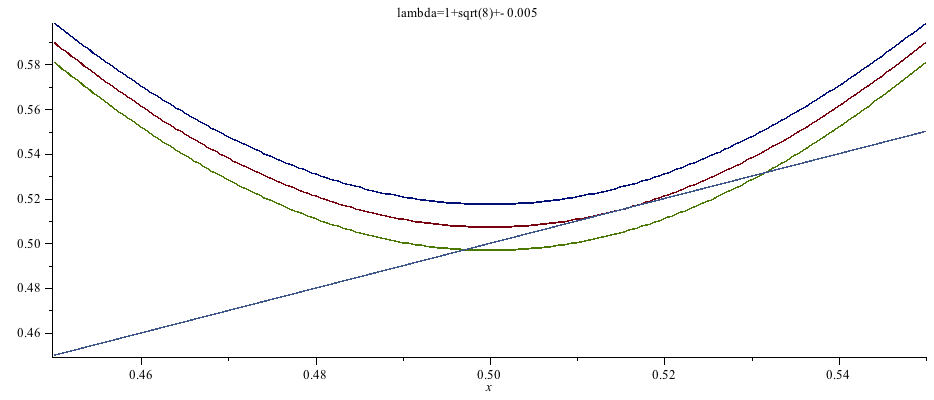
Was geschieht nun bei der Annäherung von $\mathtt{\lambda}$ an den magischen Wert von $\mathtt{1+\sqrt{8}}$. Dafür schauen wir uns am besten nochmal eine Folge von Iterationen "in dieser Gegend" an. Die drei folgenden Abbildungen sind mit $\mathtt{\lambda}$- Werten sehr nahe $\mathtt{1+\sqrt{8}}$ = 3.828427125 gerechnet, nämlich 3.826427124, 3.828227124 und 3.828407124.
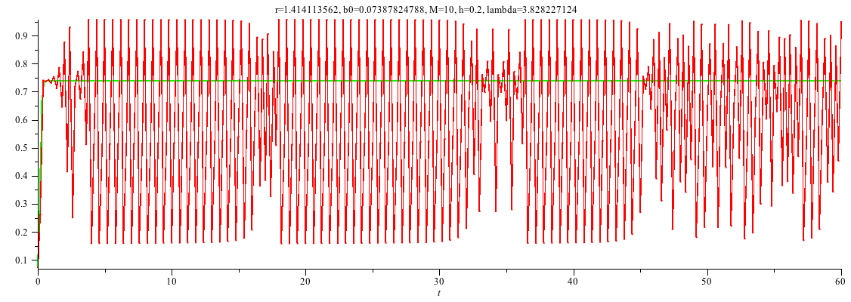
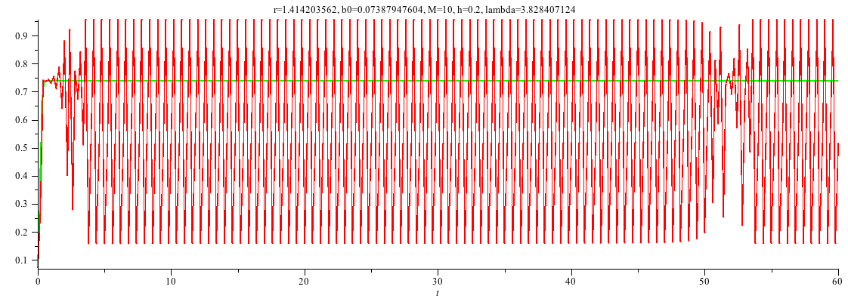
Wir sehen, dass immer mehr Regelmäßigkeit in die Iterationen einzieht, d.h. die Bereiche der Regelmäßigkeit werden immer größer, aber brechen auch wieder zusammen; man nennt dieses Verhalten des Auftretens regelmäßiger Phasen Intermittenz (15), die regelmäßigen Phasen werden auch als "laminare Phasen" (16) bezeichnet. Es gibt noch keinen Fixpunkt, der als Attraktor wirken könnte (die Ableitung von g ist betraglich noch größer 1), aber man ahnt schon sein Kommen.
Interessant auch, dass in allen Diagrammen das Zusammenziehen der Amplitude nach einer laminaren Phase gerade in Höhe der kontinuierlichen Lösung (grün) erfolgt.
Vielfach begründet man die zeitweisen Regelmäßigkeiten damit, dass sich die Iterationen, wie das nächste Bild zeigt, zwischen 1. Winkelhabierender, also der Tangente, und der nahen Kurve "hindurchzwängen" muss und so zu einer gewissen Regelmäßigkeit gezwungen ist. Diese Enge nennt man dann auch Intermittenzkanal.

Diese Abbildung zeigt eine grafische Iteration für $\mathit{\lambda = 1 + \sqrt{8} - 0.001}$ der Funktion g3.
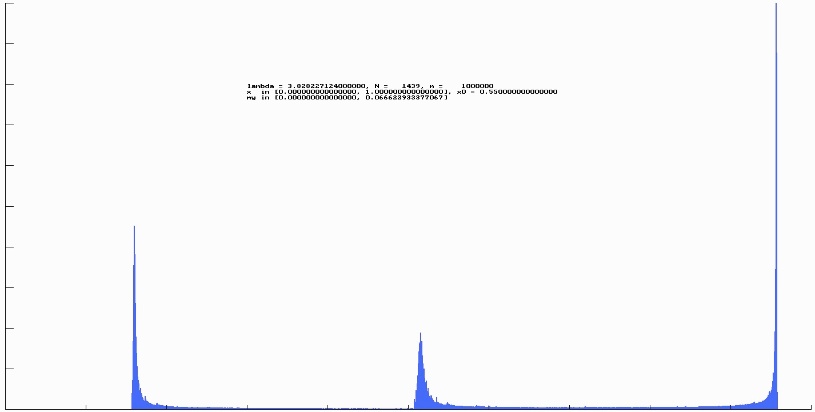
An dieser Stelle lohnt sich auch wieder der Blick in das Histogramm. Für $\mathtt{1+\sqrt{8}}$ zeigt sich ein "cleanes" Diagramm mit den 3 gleich hohen Peeks bei den im Anhang (4) angegebenen Werten für den attraktiven 3er Zyklus.
Interessant wird es nun bei den $\mathtt{\lambda}$- Werten, die ich oben bei den 3 Zeitreihen zugrunde gelegt habe (also kleiner als $\mathtt{1+\sqrt{8}}$).
Für $\mathtt{\lambda}$ = 3.828407124:

Für $\mathtt{\lambda}$ = 3.828227124:
Und für $\mathtt{\lambda}$ = 3.826427124:

Sehr schön zu erkennen, wie mit größer werdendem Abstand von $\mathtt{\lambda}$ zu $\mathtt{1+\sqrt{8}}$ die scharfen Peeks zerfließen und sich ein badewannenförmiger "Bodensatz" ausbildet. Dies stellt nochmals auf andere Weise die größer werdende Dichte der Orbitpunkte in der Nähe der Austrittspunkte der 3 attraktiven Äste dar.
Wir kommen jetzt auf das Thema Fenster zurück. Man kann nämlich die Anzahl der Fenster zu einer vorgegebenen Periode p berechnen [6], zumindest wenn p eine Primzahl ist, gilt:
$\texttt{Anzahl der Fenster(p)}\mathtt{=\frac{2^{p-1} - 1}{p}}$
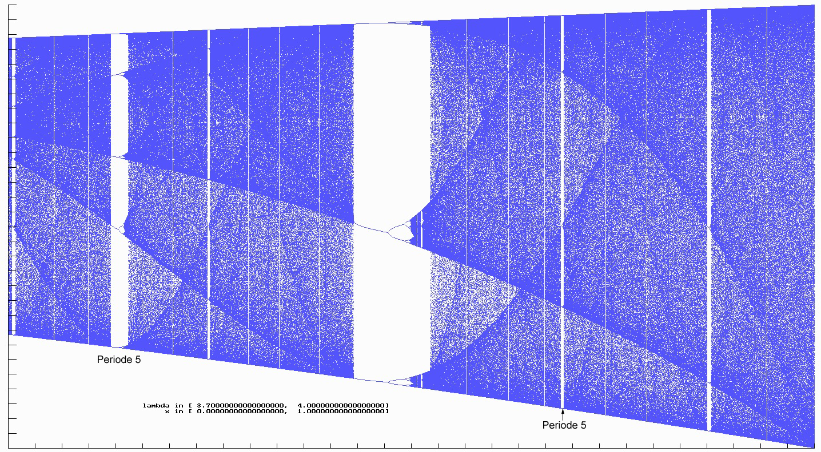

Zum Abschluss dieses Abschnittes noch der Begriff der "sensitiven Abhängigkeit von den Parametern" (20), der darauf Bezug nimmt, dass Parameter der Aufgabe (hier z.B. $\mathtt{\lambda}$) bei geringfügiger Änderung völlig andere Ergebnisse erzeugen (Chaos oder Periodizität).
Das Genie beherrscht das (deterministische) Chaos
Definition:
Eine Abbildung $\mathtt{f: J \rightarrow J \texttt{, J Intervall in }}\mathbb{R}$, heißt chaotisch, wenn folgende 3 Bedingungen gelten:
a) f hat eine sensitive Abhängigkeit von den Anfangsbedingungen
b) f ist topologisch transitiv (was bedeutet, dass man durch Iteration mittels f von einem Startwert aus in beliebige andere Bereiche von J kommen kann)
c) periodische Punkte liegen dicht in J.
Die Eigenschaft b) ist eine Zusammenhangsaussage für J, die bedeutet, dass J nicht in zwei offene Teilmengen zerlegt werden kann, die f jeweils in sich abbildet.
Oft wird im Gegensatz zum deterministischen Chaos das stochastische Chaos genannt. Dabei spielt der Zufall die entscheidende Rolle, der Unterschied ist etwa genauso wie zwischen Pseudozufallszahlen und tatsächlich zufälligen Zahlenwerten.
Feigenbaum und Mandelbrot
In meinem Artikel über die Monte Carlo Methoden habe ich die Fläche des Apfelmännchens (= Mandelbrotmenge) numerisch annähernd berechnet und dort erläutert, wie die fraktale Menge des Apfelmännchens überhaupt definiert ist. Über die Tatsache hinaus, dass sowohl Feigenbaum als auch Mandelbrot fraktale Mengen definiert und untersucht haben, gibt es einen direkten mathematischen Zusammenhang zwischen den beiden auf den ersten Blick sehr unterschiedlich aussehenden Mengen. Man kann nämlich durch eine Koordinatentransformation eine Zuordnung zwischen den Koordinatenachsen $\mathtt{\lambda}$ des Feigenbaumdiagramms und dem x der komplexen Ebene herstellen (im Sinne von Realteil). Zur Erinnerung, der Mandelbrotmenge liegt die Gleichung fc(z) = z2 + c zugrunde (z und c komplexe Zahlen) und die Mandelbrotmenge ist die Menge aller c für die die Iteration zn+1 = fc(zn), z0 = 0 beschränkt bleibt. Der Realteil von fc ist x2 + cx und die Zuordnung definiert sich mit Hilfe einer linearen Transformation, nennen wir sie $\mathtt{FM(x) := \frac{1}{2} - \frac{x}{\lambda}}$. Ebenso gebraucht wird die Umkehrabbildung $\mathtt{FM^{-1}(x) := \lambda (\frac{1}{2} - x)}$. Dann bildet man FM-1 º g º FM (x) was sich zu $\mathtt{x^2 + \frac{\lambda}{2} - \frac{\lambda^2}{4}}$ ausrechnet. Somit ist $\mathtt{c_x(\lambda)= \frac{\lambda}{2} - \frac{\lambda^2}{4}}$. Folgende Tabelle stellt ausgewählte Werte gegenüber.
| $\mathtt{\lambda}$ |
cx |
| 1 |
1/4 |
| 3 | -3/4 |
| $\mathtt{1+\sqrt{6}}$ | -1 1/4 |
| 3.5440903595 | -1.36809 |
| $\mathtt{1+\sqrt{8}}$ |
-1 3/4 |
| 3.84149900 | -1.768529154 |
| 4 | -2 |
Bei der folgenden Grafik wurde das Feigenbaumdiagramm gespiegelt und gemäß cx($\mathtt{\lambda}$) gezerrt, damit man es unter der Mandelbrotmenge anordnen und die zueinander gehörigen Punkte senkrecht verbinden kann.
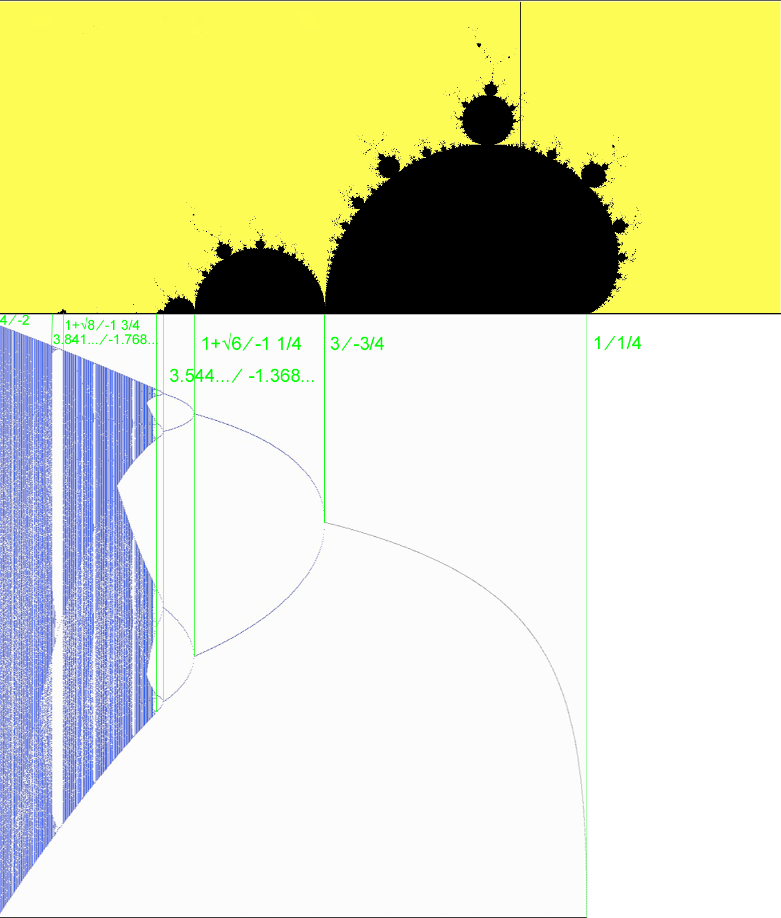
Vor dem schrägen Schrägstrich ⁄ steht der Wert des Feigenbaumdiagrammes, dahinter der zugehörige Realteil der Mandelbrotmenge.
Nachwort? Nein, kein Nachwort, aber eine Schlussbemerkung. Viele der genannten Autoren weisen darauf hin, dass dieser Zweig der Mathematik ohne Computer Science (nennen wir es mal so) nicht hätte erforscht werden können. Wie wahr. Auch ich kann mich dem nur anschließen und muss auf dem technischen Standard des Jahres 2014 (ein Laptop, ein Pascal-Compiler und Maple 17) alle bewundern, die in den 60er und 70er Jahren des letzten Jahrhunderts mit den seinerzeit vorhandenen Mitteln geforscht haben. Bei allen Berechnungen und Darstellungen in diesem Aufsatz und seinen Anhängen konnte ich die Werkzeuge praktisch vom Wohnzimmertisch aus eher spielerisch einsetzen, ohne dass sich größere oder gar unüberwindliche Schwierigkeiten zeigten - was für die Qualität und den hohen Reifegrad der Werkzeuge spricht.
Es hat Spaß gemacht!
Literaturverzeichnis und anderes
Das Buch enthält eine komplette Theorie der log. Gleichung und ist als mathematisches Standardwerk hierzu anzusehen.
[2] - Deterministic Chaos, H.G.Schuster, W.Just, WILEY-VCH
Grundlage vieler anderer Veröffentlichungen, Abriss der Renormierungstheorie, umfangreiches Beispielmaterial aus der Physik
[3] - Chaostheorie, Otto Loistl, Iro Betz, R. Oldenbourg Verlag
Umfangreiche Einführung der Grundbegriffe
[4] - Feigenbaum Universalität: Beschreibung und Beweisskizze, U. Kirchgraber und N. Sigrist, Zürich, 1985, aus dem Internet
Sehr gute, interessante geometrische Interpretation der Renormierung
[5] - Fractal Geometry, Kenneth Falconer, WILEY
Ausführliche Einführung fraktaler Dimensionen und Geomertie, Umfangreiche Betrachtung mathematischer und physikalische Beispiele
[6] - Die logistische Gleichung - ein Weg ins Chaos, Facharbeit LK Mathematik, Andreas Schmid
Gut strukturierte Darstellung vieler Phänomene der log. Gleichung
[7] - Chaostheorie - Die logistische Gleichung, Facharbeit Mathematik, Thomas Soller
Gut strukturierte Darstellung vieler Phänomene der log. Gleichung
[8| - Numerische Verfahren für Differentialgleichungen, Steffen Börm
[9] - Chaos im Universum, Joachim Bublath, Droemer Verlag
Populärwissenschaftliche Einführung
[10] - Fractals for the Classroom, Part 2, Peitgen, Jürgens, Saupe, Springer-Verlag
Eine Fülle von Darstellungen und phänomenologischen Beschreibungen
[11] - An Introduction to Caotic Dynamical Systems, Second Edition, Robert L. Devaney, ABP
Geht weit über eine Einführung hinaus, teilweise sehr ähnlich zu [1]
Liste der Anhänge
(0) - Mathematische Herleitungen zur kontinuierlichen logistischen Differentialgleichung.
(1) - Die Diskretisierung der kontinuierlichen logistischen Gleichung
(2) - Die Transformation der diskretisierten logistischen Gleichung
(3) - Theoretische Ergebnisse zur n-Periodizität und Attraktion
(4) - Praktische Ergebnisse zur n-Periodizität und Attraktion
(5) - Theoretische Überlegungen zu den Feigenbaumkonstanten
(6) - Theoretische Aussagen zum Lyapunow-Exponent
(7) - Gütekriterien numerischer Verfahren
Im Laufe des Aufsatzes berechnete Größen (alle näherungsweise):
| Bezeichnung |
berechneter Wert |
Wert aus Literatur/Internet |
| 1. Feigenbaumkonstante $\mathtt{\delta}$ |
4.6692015933429105619 (Methode 1, Eigenwert) 4.669201609102831 (Methode 2, iterativ) |
4.66920160910299067185 |
| 2. Feigenbaumkonstante $\mathtt{\alpha}$ |
2.5029078730676846833 | 2.50290787509589282228 |
| Akkumulationspunkt (Feigenbaumpunkt) $\mathtt{\lambda}$-2∞ = $\mathtt{\Lambda}$-2∞ (2-Zyklus) | 3.569987070 (Methode 1, aus geom. Reihe) 3.569945671870880664 (Methode2, iterativ) |
3.5699456 |
| $\mathtt{\lambda}$-20 (1-Zyklus Anfang) | 1 | |
| $\mathtt{\lambda}$-21 (2-Zyklus Anfang) | 3 | |
| $\mathtt{\lambda}$-22 (4-Zyklus Anfang) | $\mathtt{1+\sqrt{6}}$ | |
| $\mathtt{\lambda}$-23 (8-Zyklus Anfang) | 3.5440903595 | |
| $\mathtt{\Lambda}$-21 | $\mathtt{1+\sqrt{5}}$ | |
| $\mathtt{\Lambda}$-22 | 3.4985616993 | |
| $\mathtt{\Lambda}$-23 | 3.554640863 | |
| $\mathtt{\lambda}$-30 (3-Zyklus Anfang) | $\mathtt{1+\sqrt{8}}$ | |
| $\mathtt{\lambda}$-31 (3-Zyklus Ende) | 3.8414990075435078463 |
Berechnungen und Grafiken wurden mit Maple und Geogebra sowie der Pascal Entwicklungsumgebung FPC erstellt.
Ich füge einen Großteil der Maple-Prozeduren und die Pascalprogramme zur Zeichnung des Feigenbaumdiagrammes und des Histogrammes in einer ZIP-Datei hinzu. Die Prozeduren und das Programm sind "quick and dirty" erstellt und kaum kommentiert und in keiner Weise aufbereitet. Trotzdem sollte man erkennen können, was sie tun und wie sie arbeiten. Folgende Tabelle stellt die Namen und eine kurze Beschreibung des Inhaltes gegenüber.
| Dateiname |
Inhalt |
| bifurkation_x1/2.mw |
Betrachtungen und Abbildungen zu $\mathtt{g^n(\lambda, \frac{1}{2})}$ |
| bifurkation.mw |
Betrachtungen und Abbildungen zu gn(x) |
| disk_log_DGl.mw | Eulerverfahren für die logistische Differentialgleichung |
| FeigenMandel.mw | Transformation von der log. Gleichung zur Mandelbrotmenge |
| kont_log_DGl.mw | Lösung der kontinuierlichen logistischen Gleichung |
| lambdamu.mw | 2 Transformationen von $\mathtt{\lambda}$ nach $\mathtt{\mu}$ |
| lamdel.mw | iterative Berechnung von $\mathtt{\delta}$ und $\mathtt{\Lambda_n}$ |
| logGl.mw | Iterationen mit der logistischen Gleichung |
| lyapunov.mw | Berechnungen zum Lyapunov-Exponenten |
| LyapunowSpezial.mw | Spezialfälle des Lyapunov-Exponenten |
| Pfad.mw | Prozeduren zum Berechnen des Pfades, zum Shiften und zum Vergleichen zweier Pfade gemäß Metzler [1] |
| Reno.mw | Renormierungen vom Typ 1 und 2 |
| Tangentenbifurkation.mw | Grafiken zur Tangentenbifurkation |
| TransLog.mw | Transformation zur logistischen Gleichung |
| TransLogUebung | Transformation zur logistischen Gleichung |
| Verdopplungsoperator2.mw | Verdopplungsoperator im Bereich [0, 1] |
| Verdopplungsoperator3.mw | Verdopplungsoperator im Bereich [-1, 1] |
| VerdopplungsoperatorMy.mw | Bestimmung des Fixpunktes g des Verdopplungsoperators tau mit Newton, Berechnung von delta als Eigenwert der Linearisierung von tau, Berechnung von alpha aus g. Achtung: Viele Berechnungen schließen mit dem Doppelpunkt ab, da ihr Ergebnis wegen seiner Länge nicht darstellbar ist! |
| Feigen.pas | Darstellung des Feigenbaumdiagramms, Pascalprogramm |
| Histo.pas | Berechnung und Darstellung eines Histogramms |
| GraphikUnit.pas | Zugehöriges Grafiktool |
| TimeSrv.pas | Zugehöriges Tool zur Zeitmessung |
LogGl.zip